频率波数域matlab,频率-波数域方法的发展及其在台阵数据分析中的应用

0 引言

自1960年起，地震台阵作为一种新型的地震学研究工具，已经广泛应用于不同类型波场信号的检测及地球内部不同尺度结构的成像(

传统的F-K方法(

各种不同类型台阵的陆续建设，为F-K分析提供了大量的数据支持，使得该方法在理论和实践中都得到了极大的发展。人们对F-K方法的不断改进(

1 F-K分析方法

从原理上来说，F-K方法是基于频率波数域功率谱密度函数(F-K PSDF)的计算，将台阵观测信号从时间-空间域转换到频率-波数域，从而获取入射波场能量在不同慢度和方位角的分布。根据窗函数的不同，可分为聚束法(

1.1 F-K谱

$

E{P_b}({\rm{f,k}}) = \sum\limits_{n,m = 1}^N {{\phi _{nm}}} \exp \left[ {{\rm{i}}k\left( {{{\rm{X}}_m} - {{\rm{X}}_n}} \right)} \right]

$

(1a)

$

E{P_m}({\rm{f,k}}) = {[ {\sum\limits_{n,m = 1}^N {\phi _{nm}^{ - 1}} \exp \left[ {{\rm{i}}k\left( {{{\rm{X}}_n} - {{\rm{X}}_m}} \right)} \right]^{ - 1}} }

$

(1b)

此处，f表示频率，k为波数，N是台阵中所包含的地震台站数目，φnm是第n和第m个台站记录之间的互功率谱，Xn和Xm分别为第n和第m个台站的坐标。

上述两种方法最主要的不同是窗函数。聚束法在波数k0的窗函数可表示为

$

{W_b}(k,{k_0}) = {\rm{ }}\frac{1}{{{N^2}}}\sum\limits_{n,m = 1}^N {\exp \left\{ {i\left( {k - {k_0}} \right)\left( {{X_n} - {X_m}} \right)} \right\}}

$

(2)

最大似然法的窗函数为

$

{W_m}(k,{k_0}) = {\rm{ }}\left| {\sum\limits_{j = 1}^N {{A_j}(f,{k_0})} } \right|{W_b}(k,{k_0})

$

(3)

其中

$

{A_j}(f,{k_0}) = \sum\limits_{n = 1}^N {{{({\phi _{jn}}\exp\{ i{k_0}({X_j} - {X_n})\} )}^{ - 1}}} {\rm{/}}\sum\limits_{j,n = 1}^N {{{({\phi _{jn}}\exp\{ i{k_0}({X_j} - {X_n})\} )}^{ - 1}}}

$

(4)

由公式(2)~(4)可以看出，聚束法的窗函数仅与台阵形状有关，相当于使用了固定的空间滤波器，最大似然法的窗函数不仅依赖于台阵形状，而且取决于数据的质量，相当于一种优化的空间滤波器，是一种非线性方法。众多研究表明，聚束法提供了频率-波数功率谱渐进无偏的一致估计，而最大似然法给出了频率-波数功率谱的最大似然估计，具有更高的分辨率(

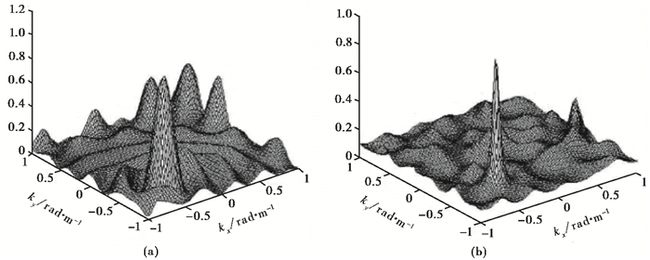
图 1

图 1 两种F-K方法估计的三维频率-波数谱。(a)聚束法；(b)最大似然法(

在频率f一定时，假定F-K图像的峰值出现在波数坐标(kx，ky)，则此处对应的视速度为

$

{v_{\max}} = {\rm{ }}\frac{{2\pi f}}{{\sqrt {k_x^2 + k_y^2} }}

$

(5)

$

{\theta _{\max}} = \tan^{ - 1}\left( {\frac{{{k_x}}}{{{k_y}}}} \right)

$

(6)

1.2 基于非相干平均法的F-K方法

上面提到的两种F-K方法主要应用于窄带信号的计算。从窄带拓展到宽频带有两种方法，包括相干信号平均法(the coherent averaged signal method；

基于宽频带非相干平均法的最大似然F-K谱(加入了对角加载因子)是若干个离散频率点的谱总和，可表示为

$

P\left( {f,k} \right) = \sum\limits_{j = 1}^L {[ {\sum\limits_{n,m = 1}^N {\phi _{nm}^{ - 1}\left( {f,k,\alpha } \right)\exp {{\left[ {ik\left( {{X_n} - {X_m}} \right)} \right]}^{ - 1}}} } }

$

(7)

其中，L是离散频率点的个数，α表示DL参数。

v=3.33km/s和v=4.16km/s附近的Rg和Lg震相，但也有一定的差异，相对于前者，后者能够检测到更多不同类型的源，如慢度较小的次级体波噪声源。

图 2

图 2 (a) 用最大似然法法获取的F-K谱；(b)基于非相干平均法获取的F-K谱(

1.3 去除台阵响应函数的F-K方法

在过去的数十年间，全球范围内发展了多种不同类型的台阵用于地震学的研究，如加拿大的十字形黄刀台阵(the Yellow knife Array，即YKA)、美国的大孔径台阵(the Large Aperture Seismic Array，即LASA)、德国的宽频带大孔径台阵((the Large-aperture Grafenburg Array，即GRF)、中国的上海佘山台阵等。台阵的布局是影响台阵对不同频率和慢度信号分辨能力的重要因素，可以用台阵响应函数(ARF)定量表示。对于一个给定的台阵，一些通用的准则用于衡量孔径、地震台数、台间距、台阵几何形状等因素对台阵响应函数的影响(

台阵响应函数在波数k0处可以表示为(

$

ARF = {\rm{ }}\frac{1}{{{N^2}}}\sum\limits_{n,m = 1}^N {\exp \left\{ {i\left( {k - {k_0}} \right)\left( {{X_n} - {X_m}} \right)} \right\}}

$

(8)

利用RL反卷积方法可以去掉台阵响应函数的影响，从而获取更高分辨率的F-K谱。

RL反卷积方法可以表示为

$

E{\delta ^{m + 1}} = E{\delta ^m}\left( {{A^{\rm{T}}}\frac{g}{{AE{\delta ^m}}}} \right)

$

(9)

其中，A表示台阵响应函数，m是迭代次数，g为原始的F-K谱，Eδm是经过m次迭代后的正则化解。

CLEAN算法最初用于天文学的研究，原理是通过不断迭代反卷积去掉点源(point spread function，即PSF；

去除PSF旁瓣后的互功率谱矩阵可以表示为

$

C_{PSF}^{i + 1} = {C^i} - \phi P_{\max }^i{w_{\max}}w_{\max }^*

$

(10)

其中，Ф是约束因子，控制去除能量所占的比例(例如，Ф=0.05表示去除最强信号源能量的5%)，wmax为每对互功率谱矩阵的权重因子矢量，wmax*是权重因子矢量的复共轭，Pmax代表功率谱中的最大值。

去除最强信号源后，重构功率谱为

$

{P_{CLEAN}}\left( k \right) = \sum\limits_{i = 1}^M {\phi P_{\max }^i}

$

(11)

其中，M表示迭代次数，ФPmaxi是第i次迭代时清除掉的能量。

最后得到的F-K谱为

$

{P_{PSF}}\left( k \right) = {w}_B^*\left( k \right){C}_{PSF}^M\left( f \right){w_B}\left( k \right) + {P_{CLEAN}}\left( k \right)

$

(12)

2 F-K方法在台阵数据分析中的应用

本文主要就F-K方法在检测微弱信号源、分析噪声特征、提取面波频散曲线、评估台阵设计优劣等4方面的应用进行综述。

2.1 检测不同类型的微弱信号源

地震台阵能够在一定条件下记录到一致性较好的波形，采用F-K方法处理台阵数据，可以区分不同方向入射波场的能量分布，聚束具有相同频率、相同慢度但不同入射方向的信号，因而能够大幅度降低全球地震、核爆等不同类型事件的检测下限，这对于识别被强震掩盖的微弱事件具有良好的效果。

2.2 分析微震噪声特征

美国LASA于1965年完成建设并投入使用，使得利用F-K方法在进行噪声特征分析上取得了一系列突破(

随后，越来越多不同类型台阵的建立更加丰富了F-K方法在噪声分析中的应用。

基于众多单个台阵的研究结果，

图 3

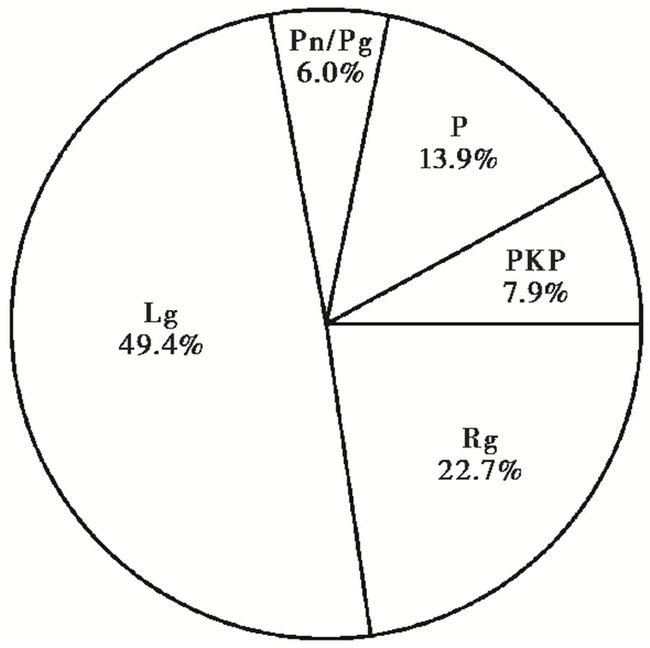
图 3 一个圆形台阵的F-K慢度分布示例图

几个不同半径的圆圈分别对应于不同的慢度：4.4s/deg，13.9s/deg，27.8s/deg，37.1s/deg(

图 4

图 4 利用18个台阵2007~2008年的噪声记录统计获得的相速度分布(

2.3 提取面波频散曲线

地震面波在传播过程中最重要的特点之一是存在频散现象，这一特性是由地下介质的结构和非弹性决定的。因此，利用面波的频散曲线，通过合适的反演方法，便可以获取地下介质的速度结构。假设面波是噪声的主要成分，利用F-K方法将空间-时间域的噪声记录转换到频率-波数域后，不同频率的面波在二维波数空间上会出现相应的峰值; 确定该峰值的位置即可得到波数，从而能够计算出不同频率面波的相速度，获取面波的频散曲线。如果研究三分量的连续噪声记录，便可以同时提取瑞雷波和勒夫波的频散曲线。

2.4 评估台阵设计的优劣

台阵作为地震观测网的重要组成部分，引起了地震学家的高度重视。出于不同的观测目的，如核爆识别，绘制区域地震活动图，监测远震等，全球范围内已经建设或正在筹建各种不同类型的台阵。台阵设计对于节约成本，确保各种监测目的实现的重要性不言而喻。作为一种重要的台阵数据处理方法，F-K谱的分辨率是衡量台阵布局是否合理的有效工具。

台阵布设中需要考虑到台阵形状、测点数量、孔径大小、台间距等多种因素，可以用台阵响应函数在频率-波数域的值来定量描述这些因素的影响。

3 讨论与展望

本文介绍了F-K分析的基本原理及其各种改进方法，并综述了F-K方法在检测微弱信号源、噪声特征分析、提取面波频散曲线、台阵设计等4方面的应用。总体来说，F-K台阵处理方法具有较高的分辨率，其方法的不断改进也在拓宽它的应用领域。

(1) 本文总结了几种F-K分析方法，包括传统的聚束法和最大似然法，基于非相干平均法的F-K方法，利用Richardson-Lucy(RL)反卷积和CLEAN-PSF去除台站响应函数的F-K法。传统的聚束法和最大似然法的分辨率有限，容易漏检一些微弱的噪声源；而基于非相干平均法的F-K法能够拓宽所检测噪声源的频带，从而识别更多的微震噪声。然而，众多研究表明，台阵里有限的采样点及不合理的排列方式往往会限制F-K图像的空间分辨率及其对不同频率面波的分辨能力。以上几种方法均没有考虑到台阵布局对F-K谱的影响，利用它们对不规则的台阵进行F-K成像时会影响结果的分辨率。去除台阵响应函数的F-K分析方法能够弥补上述几种方法的不足，可以在一定程度上提高F-K成像的分辨率，使得如圆形、L型、十字型或随机分布的台阵都能够得到有效利用。

(2) 除了文中所述的应用之外，考虑到F-K分析能够降低地震等事件的识别下限，利用多个台阵便可以实现对微小地震的精定位。此外，F-K分析能够提高得微弱信号的信噪比，已经在定位近地表散射源中有了初步的应用，如何将其用于识别更多的反射波和散射波等微弱信号，从而拓宽地震台阵在地球内部的精细结构成像方面的应用，需要更深入的探索。

(3) 像其他大多台阵方法一样，F-K分析是基于平面波入射的假设，台阵下方的各向异性有可能会改变波前并破坏信号的相干性，从而改变F-K分析的结果。研究高频信号时采用的小孔径台阵的地下介质往往比较均匀，因而获得的入射波方位角较稳定，但由于高频微震信号源的变化，导致其视慢度值不稳定，可以通过滑动窗法获取高频噪声的时空变化特性；研究低频信号时需要台间距相对较大的台阵，视慢度值较稳定，但可能由于传播路径上的横向不均匀性而造成方位角的偏离，长时间叠加可能有助于稳定F-K图像的结果。

致谢:

审稿专家对本文提出了宝贵的修改意见和建议，谨表谢忱。