深度神经网络的不确定性（中）

不确定度估计方法

不确定度的来源很多，我们无法完全去除不确定度。而不确定度本身也很难精确计算，因为不同的不确定度不能统一精确建模而且很多时候甚至是未知的。通常情况下，不确定度的估计方法可以基于使用dnn的数量和本质分为四种不同类型。

• Single Deterministic Methods是在一个确定性网络中基于单个前传通路给出预测。不确定度的量化要么用额外的方法推导，要么直接从网络预测。
• Bayesian Neural Networks覆盖了所有随机dnn的类型，即同一个样本两次前传得到不同结果。
• Ensemble Methods在inference阶段结合不同的确定性网络的预测。
• Test Time Augmentation基于单个确定性网络给出预测，但是在测试时扩大输入数据来生成多个预测再用来估计确定性。

figure 3展示了四种不同的不确定性量化方法。

figure 4展示了区别四种方法的基本原理。

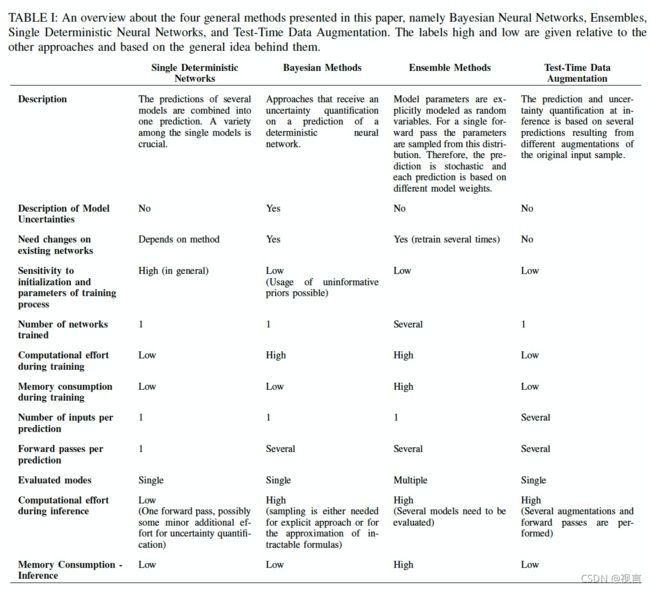
table 1总结了各种方法的主要属性，例如复杂度，计算量，内存消耗，灵活性等。

A.Single Deterministic Methods

对于确定性神经网络来说参数是确定的，重复forward通路获得相同的结果。单个确定性网络可以粗糙地分为显式地建模单个网络来量化不确定度的方法，以及在网络的预测上使用额外的组成来给出不确定度估计的方法。对第一种类型，不确定度的量化影响了训练过程和网络预测， 后一种类型一般应用在已经训练好的网络上。因为训练好的网络在这些方法中没有被修改，所以他们对网络预测没有影响。下面我们称这两种方法为内部和外部不确定性量化方法。
1）内部不确定性量化方法
许多内部不确定度量化方法预测预测结果的分布参数，而不是直接最大的逐点后验分布估计。通常这种网络的损失函数都会考虑真实分布和预测分布的差异。尝试模仿网络贝叶斯建模的行为，其输出的分布可以解释为模型不确定度的量化。这个预测就是给定预测分布的期望值。
对于分类任务，通常情况下输出表示类别的概率。这些概率是多类softmax函数的结果

$$\begin{gathered} \text{softmax}:{\mathbb{R}}^K\to \left\{z\in {\mathbb{R}}^K|z_i\ge 0,\sum _{k=1}^K{z}_k=1\right\} \\ \text{softmax}(z{)}_j=\frac{\exp (z_j)}{{\sum }_{k=1}^K\exp (z_k)} \end{gathered}$$
以及logits z上二分类任务的sigmoid函数
$$\begin{gathered} \text{sigmoid}:\mathbb{R}\to [0,1] \\ \text{sigmoid}(z)=\frac{1}{1+\exp (-z)} \end{gathered}$$

这些概率也可以解释为数据不确定度的预测。然而神经网络经常over-confident，softmax的输出没有很好地校准，导致不精确的不确定度估计。此外，softmax的输出是不能和模型不确定度关联的。而如果不显式地考虑模型不确定度，分布外的样本能够导致输出给出错误的置信度。例如，网络在猫和狗上训练，喂进去鸟是不会得到50%猫和50%狗的。这是因为网络从图像提取特征，即使特征不拟合猫类，那它们也可能更不拟合狗类。结果网络在猫上的概率更大。此外，relu网络和softmax输出的结合导致网络随着分布外的样本和学习到的训练集距离变大，越来越confident。figure 5展示了mnist一个数字的旋转导致高softmax值的错误预测。这个现象有人研究并提出了一种方法来避免，就是强加一个离训练集很远的均匀预测分布。

一些其他的分类方法使用一个类似的想法，就是考虑logit量级，利用狄利克雷分布。狄利克雷分布是分类分布的共轭先验，因此能够解释成分类分布上的一个分布。狄利克雷分布的密度函数定义为
$$\text{Dir}\left(\mu |\alpha \right)=\frac{\Gamma ({\alpha }_0)}{{\prod }_{c=1}^K\Gamma ({\alpha }_c)}\prod _{c=1}^K{\mu }_c^{{\alpha }_c-1},{\alpha }_c>0,{\alpha }_0=\sum _{c=1}^K{\alpha }_c,$$
其中$\Gamma$是gamma函数，${\alpha }_1,...,{\alpha }_K$称为浓度参数，标量${\alpha }_0$是分布的精度.实际上，浓度${\alpha }_1,...,{\alpha }_K$是通过一个严格正变换推出来的，例如指数函数应用到logit值。如fig 6所示，一个更高的浓度值导致一个更为尖锐的狄利克雷分布。

k个类别分布的所有类概率的集合等价于k-1维标准或概率单形。这个单纯形的每个节点表示一个概率向量，在一个类上具有完整的概率质量，节点的每个凸组合表示一个类别分布，概率质量分布在多个类上。Malinin等人认为，由于网络不熟悉数据，高模型不确定性应该导致较低的精度值，因此在整个单纯形上的分布是平坦的。与此相反，由于网络可以处理数据，但不能给出明确的类偏好，因此数据的不确定性应该以更尖锐但也更集中的分布来表示。fig6展示了不同的期望行为。狄利克雷分布被用于几种方法，如狄利克雷先验网络和证据神经网络。这两种网络类型都输出狄利克雷分布的参数，从狄利克雷分布中可以推导出描述类概率的类别分布。先验网络的一般思想已经在上面描述过了，如fig 6所示。先验网络以多任务的方式进行训练，其目标是最小化分布内数据预测与尖锐狄利克雷分布之间以及平坦狄利克雷分布与分布外数据预测之间的预期Kullback-Leibler (KL)散度。除了更好地分离分布内样本和OOD样本的主要动机外，这些方法还提高了正确预测和不正确预测置信度之间的分离。后续研究讨论了在数据不确定性较高的情况下，KL-divergence的正向定义会导致不理想的多模型目标分布。为了避免这种情况，他们使用逆向KLdivergence重新计算了损失。实验结果表明，在不确定性估计和对抗鲁棒性方面都有改进。Zhao等人通过一种新的损失函数扩展了Dirichlet网络方法，该损失函数旨在基于$L_{\infty }-norm$范数最小化期望误差的上界，即优化期望的最坏情况上界。有研究认为，使用混合狄利克雷分布在逼近后验分布时提供了更大的灵活性。因此，提出了一种网络预测K个Dirichlet分布混合参数的方法。为此, 网络 logits被优化来表达 $M$ 个Dirichlet 分布 和 约束${\sum }_{i=1}^M{\omega }_i=1$ 中 $M$ 个权重 ${\omega }_i,i=1,..,M$ 的参数. Nandy等人分析表明，对于具有高数据不确定性的域内样本，错误预测预测的狄利克雷分布通常比正确预测预测的更平坦。他们认为，这使得区分分布内和分布外的预测变得更加困难，并建议使用一个正则项来最大化分布内和分布外样本之间的差距。

证据神经网络还优化了单个狄利克雷网络的参数化。损失公式是通过使用主观逻辑推导出来的，并将对数解释为多项意见或信念，如证据或Dempster-Shafer理论中介绍的那样。证据神经网络根据类的数量设置了证据的总量，并由此得出一个不确定性值，即接受一个额外的“我不知道类”。损失被表述为基本损失的期望值，例如类别交叉熵，相对于由logits参数化的狄利克雷分布。此外，还添加了一个正则化项，鼓励网络不考虑同时为多个类提供证据的特征，例如一个圆代表6和8。正因为如此，网络并不区分数据不确定性和模型不确定性，而是学习它们是否能够给出某种预测。有研究扩展了这一想法，在收集到的证据中区分锐度和不和谐，以便更好地分离分布内和分布外的样本。为此，需要两个包含重叠类和分布外样本的显式数据集来学习正则化项。Amini等人通过在基础正态分布上学习证据正态逆伽马分布的参数，将证据神经网络的思想从分类任务转移到回归任务。Charpentier等人通过使用归一化流来学习每个类在隐空间上的分布，避免了训练过程对OOD数据的需求。一个新的输入样本被投射到这个隐空间上，狄利克雷分布是基于嵌入隐点的逐类密度参数化的。除了上述基于狄利克雷分布的方法外，还有其他几种内部方法。有人提出了一种基于训练输入数据的微小扰动和温度缩放校准的相对简单的方法，从而有效地区分分布内和分布外样本。Mo zejko等人利用了受抑制的softmax函数。它包含一个人工的常量logit，使单个logit的绝对值在softmax输出中更具决定性。Van amersfort等人表明，径向基函数(RBF)网络可以在准确性和不确定性估计方面获得具有竞争力的结果。RBF网络学习logits上的线性变换，并根据变换后的logits和被学习的类质心之间的距离对输入进行分类。Van amersfort等人使用了缩放的指数L2距离。数据的不确定度可以直接由质心之间的距离得到。通过在损失函数中包含雅可比矩阵上的惩罚，训练网络对输入空间的变化更加敏感。结果表明，该方法具有较好的分布外检测性能。在几次测试中，将该方法与5个成员的深度集成进行了比较，结果表明，这种单一网络方法在检测分布不均匀的样本方面表现至少差不多好，并提高了真阳性率。

对于回归任务，Oala等人引入了基于区间神经网络的下限和上限输出的不确定性评分。区间神经网络具有与底层确定性神经网络相同的结构，并使用确定性网络的权值进行初始化。与由标准偏差给出的不确定度的高斯表示不同，这种方法可以给出不确定度的非对称值。此外，该方法在有噪声的情况下具有更强的鲁棒性。Tagasovska和Lopez- Paz提出了一种估计数据和模型不确定性的方法。同时引入分位数回归损失函数，为数据的不确定性生成校正良好的预测区间。模型的不确定性是基于从训练数据到零的映射来量化的，这是基于所谓的标准正交认证。其目的是将模型不确定的分布外样本映射到非零值，从而可以被识别。Kawashima等人¹介绍了一种基于交叉验证(如预训练步骤)的方法，计算回归任务训练样本中的虚拟残差。利用这些残差信息扩展原始训练数据，训练实际预测器给出预测和确定性值。实验表明，虚拟残差是避免过于自信网络预测的有效工具。

2）外部不确定性量化方法
外部不确定性量化方法不会影响模型的预测，因为不确定性的评估与潜在的预测任务是分离的。此外，几种外部方法可以同时应用于已经训练好的网络，而互不影响。Raghu等人认为，当预测和不确定性量化这两项任务都用同一种方法完成时，不确定性估计会受到实际预测任务的影响。因此，他们推荐了一种“直接不确定性预测”，并建议训练两个神经网络，一个用于实际的预测任务，另一个用于预测第一个网络预测的不确定性。类似地，Ramalho和Miranda引入了一个额外的神经网络来进行不确定性估计。但与Raghu等人相比，它考虑了训练数据的表示空间，并评估了给定测试样本周围的密度。附加神经网络使用这种训练数据密度来预测主网络的估计预期是正确的还是错误的。Hsu等人在softmax输出给出的分类分布之外，通过预测每个类的总概率，在测试时检测到分类任务中的分布外样本。通过将sigmoid函数应用到网络的logit上，预测类的全概率。基于这些总概率，OOD样本可以被识别为所有类的类概率都较低的样本。

与此相反，Oberdiek等人通过在分类任务中使用梯度度量对不确定性进行量化，考虑了模型的敏感性，即模型的斜率。Lee等人应用了类似的想法，但使用了反向传播的梯度。在他们的工作中，他们提出了关于分布外和损坏输入检测的最新结果。

3）单一确定方法的总结
与许多其他原理相比，单一确定性方法在训练和评估方面计算更高效。对于训练，只需要训练一个网络，而且通常这些方法甚至可以应用在预先训练的网络上。根据实际的方法，只需要完成一个或最多两个前向传播来进行评估。底层网络可能包含更复杂的损失函数，这会减慢训练过程或需要额外训练和评估的外部组件。但总的来说，这仍然比基于集成的方法、贝叶斯方法和测试时数据增强方法所需的预测数量更有效。单一确定性神经网络方法的一个缺点是，它们依赖于单一的意见，因此可能对底层网络架构、训练过程和训练数据非常敏感。

B.Bayesian Neural Networks

贝叶斯神经网络的贝叶斯学习与学习最大化似然度相比，有能力结合可拓展性、表达力以及神经网络预测性能。这是通过推断网络参数$\theta =(w_1,...,w_K)$上的概率分布来实现的。更具体地说，给定一个训练输入-目标对$(x,y)$，通过假设参数$p(\theta |x,y)$的先验分布并应用贝叶斯定理来建模参数$p(\theta )$空间上的后验分布:
$$p(\theta |x,y)=\frac{p(y|x,\theta )p(\theta )}{p(y|x)}\propto p(y|x,\theta )p(\theta ).$$
这里，上式归一化常数被称为模型证据$p(y|x)$，定义为：
$$p(y|x)=\int p(y|x,\theta )p(\theta )d\theta .$$
一旦权重上的后验分布被估计，一个新的输入数据$x^{\ast }$的输出$y^{\ast }$的预测可以通过贝叶斯模型平均或全贝叶斯分析得到，这涉及到边缘化似然度$p(y|x，\theta )$，以后验分布：
$$p(y^{\ast }|x^{\ast },x,y)=\int p(y^{\ast }|x^{\ast },\theta )p(\theta |x,y)d\theta .$$
这种贝叶斯预测方法是全概率定律的直接应用，从原理上赋予了计算预测不确定性的能力。贝叶斯边际化的积分对于最常见的先验后验对来说是棘手的，因此通常应用近似技术。最广泛的近似，蒙特卡洛近似，遵循大数定律，通过$N$个确定性网络的平均值，$f{\theta }_1，\dots ，f{\theta }_N$，参数化为来自权重后验分布的$N$个样本，${\theta }_1，{\theta }_2，\dots ，{\theta }_N$，即：
$$y^{\ast }\approx \frac{1}{N}\sum _{i=1}^N{y}_i^{\ast }=\frac{1}{N}\sum _{i=1}^N{f}_{{\theta }_i}(x^{\ast }).$$
值得注意的例子包括贝叶斯模型选择，模型压缩，主动学习，持续学习，贝叶斯学习等方面的理论进展。虽然这个公式相当简单，但也存在一些挑战。例如，后验推断不存在闭合形式的解，因为共轭先验对于神经网络等复杂模型通常不存在。因此，通常需要近似贝叶斯推断技术来计算后验概率。然而，直接使用近似贝叶斯推断技术已经被证明是困难的，因为数据的大小和参数的数量对于深度神经网络太大了。换句话说，上述方程的积分随着数据的大小和参数的数量增加是无法计算的。此外，为深度神经网络指定有意义的先验是另一个理解较少的挑战。

总的来说，根据如何推断后验分布来近似贝叶斯推断可以把BNN分成三种类型：

• 变分推断
  变分推断通过在一族易处理的分布上优化来近似通常不易处理的后验分布。
• 采样方法
  采样方法从可以采样的实现中提供目标随机变量的表示。这样的方法是基于马尔科夫链蒙特卡洛及其拓展。
• 拉普拉斯近似
  拉普拉斯近似通过近似对数后验分布来简化目标分布，然后基于这种近似，得到网络权重上的高斯分布。

除了这三个类别外，BNN领域也有一些其他进展，一些例子是(i)近似推断技术，如阿尔法发散，期望传播，假设密度滤波等，(ii)概率规划利用现代图形处理单元，(iii)不同类型的先验，(iv) bnn的理论理解的进步，(iv)加速边缘化过程的不确定性传播技术和(v)任意不确定性的计算。

1)变分推断: 变分推断的目标是使用预先指定的分布族$q(\theta )$来推断后验概率$p(\theta |x,y)$。这里，这些所谓的变分族$q(\theta )$被定义为一个参数分布。一个例子是多元正态分布，其参数是均值和协方差矩阵。变分推断的主要思想是找到这些参数的设置，使$q(\theta )$接近感兴趣的$p(\theta |x,y)$的后验。这种对概率分布之间紧密程度的衡量是由Kullback-Leibler (KL)散度给出：
$$\text{KL}(q||p)={\mathbb{E}}_q\left[\text{log}\frac{q(\theta )}{p(\theta |x,y)}\right].$$
由于后验$p(\theta |x,y)$， 上式中的kl散度不能直接最小化。用证据下界(ELBO)替代，优化一个KL散度等于常数的函数。对于参数$p(\theta )$的给定先验分布，ELBO由下式给出：
$$L={\mathbb{E}}_q\left[\log \frac{p(y|x,\theta )}{q(\theta )}\right]$$
而KL散度为：
$$\text{KL}(q||p)=-L+\log p(y|x)$$
Hinton和Van Camp率先提出了bnn的变分方法，他们推导出了神经网络后向分布的对角高斯逼近(在信息论中表达为——最小描述长度)。在20世纪90年代，Barber和Bishop提出了另一个值得注意的扩展，其中选择了全协方差矩阵作为变分家族，作者演示了如何为神经网络优化ELBO。一些现代方法可以被视为这些早期工作的延伸，其重点是如何将变分推理扩展到现代神经网络。
当前方法的一个明显方向是使用随机变分推断(或蒙特卡洛变分推断)，其中使用小批数据执行ELBO的优化。Graves等人利用高斯先验提出了与随机变分推断的第一个联系。2015年，Blundell等人引入了随机变分推断对非高斯先验的进一步扩展Bayes By Backprop，并演示了如何使随机梯度无偏。值得注意的是，Kingma等人引入了局部重新参数化技巧来减少随机梯度的方差。其中一个关键概念是将神经网络的损失函数重新表述为ELBO。因此，通过对训练程序进行一定的修改，可以间接优化难以处理的后验分布，并使变分推断与反向传播兼容。这些扩展广泛地关注随机变分推断的脆弱性，这是由初始化的敏感性，先验定义和梯度的方差引起的。Wu等人最近已经解决了这些局限性，他们使用了分层先验，并确定性地逼近了变分分布的矩。上述工作通常假设平均场近似为变分族，忽略了参数之间的相关性。为了使更具有表现力的变分分布在深度神经网络中可行，一些著作提出了使用矩阵正态分布或更具有表现力的变体来推断，其中协方差矩阵被分解为较小矩阵的克罗内克乘积或低秩形式加上一个正对角矩阵。对表达后验分布的一个显著贡献是使用归一化流，这是一种分层概率分布，其中应用了一系列可逆变换，从而将简单的初始密度函数转换为更复杂的分布。有趣的是，Farquhar等人认为平均场近似不是一个限制性的假设，分层加权相关可能不如捕获深度相关重要。虽然Farquhar等人的主张仍然是一个悬而未决的问题，但平均场近似在较小的计算复杂性方面具有优势。例如，Osawa等人证明了变分推理可以使用多个gpu扩展到ImageNet大小的数据集和架构，并提出了数据增强、动量初始化和学习率调度等实用技巧。

变分方法的成功之一是将现有的深度学习随机元素作为变分推断。一个广为人知的例子是蒙特卡洛Dropout (MC Dropout)，其中Dropout层被制定为伯努利分布随机变量，训练一个带有Dropout层的神经网络可以近似地执行变分推断。MC dropout的一个主要优点是，通过激活dropout，不仅可以在训练时，而且可以在测试时计算预测不确定性。通过这种方式，一旦使用dropout层训练神经网络，实现的工作量就可以保持在最低限度，从业者不需要专家知识来推理不确定性——作者将其成功归因于某些标准。该方法的实用价值 也在一些著作中得到了证明，并产生了不同的扩展(评估不同dropout mask的使用 ，例如卷积层，或通过将预测不确定性的表示改变为模型和数据不确定性）。在相关文献中也提出了基于类似思想的方法，即随机删除某个节点的传入激活，而不是删除所有后续节点的激活，这种方法称为drop connect。研究发现，这在不确定性表示上更稳健，尽管研究表明两者的结合可以导致检验预测中更高的准确性和鲁棒性。最后，文献中进一步提出了变分推理与Adam、RMS Prop和批归一化之间的联系。

2)采样方法: 采样方法，或通常称为蒙特卡洛方法，是贝叶斯推理算法的另一个家族，没有参数模型表示不确定性。具体地说，抽样方法使用一组从分布中提取的假设(或样本)，并提供一个优势，即表示本身不受分布类型的限制(例如，可以是多模态或非高斯分布)，因此得到的概率分布是非参数的。这一领域的流行算法有粒子滤波、抑制抽样、重要抽样和马尔可夫链蒙特卡洛抽样(MCMC)。
在神经网络的情况下，MCMC经常被使用，因为拒绝和重要性采样等替代方法对于这样的高维问题是低效的。MCMC的主要思想是通过状态空间中的转换从任意分布中采样，这种转换由当前状态的记录和旨在估计目标分布(如真实后验)的候选分布控制。为了解释这一点，让我们开始定义马尔可夫链:马尔可夫链是随机变量$x_1，\cdots ,x_T$的分布，它遵循状态转移规则:
$$p(x_1,\cdots ,x_T)=p(x_1)\prod _{t=2}^{T}p(x_t|x_{t-1}),$$
也就是说，下一个状态只依赖于当前状态，而不依赖于任何其他更前状态。为了从真正的后验中抽取样本，MCMC采样方法首先以迭代和马尔可夫链的方式生成样本。然后，在每次迭代中，算法决定接受或拒绝样本，其中接受的概率由一定的规则决定。这样，当产生越来越多的样本时，它们的值就可以接近期望的分布。
哈密顿蒙特卡罗或混合蒙特卡罗(HMC)²是MCMC采样方法的一种重要变体(尼尔斯首创用于神经网络)，通常被认为是贝叶斯推断的黄金标准。该算法的工作原理如下:(i)首先初始化一组参数$\theta$(随机或以用户特定的方式)。然后，对于给定的总迭代次数，(ii)不是随机游走，而是采样一个动量向量——一个辅助变量$\rho$，参数$\theta$的当前值通过哈密顿动力学更新：
$$H(\rho ,\theta )=-\text{log}p(\rho ,\theta )=-\text{log}p(\rho |\theta )-\text{log}p(\theta ).$$
定义势能($V(\theta )=-logp(\theta )$和动能$T(\rho |\theta )=-\text{log}p(\rho |\theta )$，汉密尔顿方程的更新步骤由下式控制，
$$\begin{gathered} \frac{d\theta }{dt}=\frac{\partial H}{\partial \rho }=\frac{\partial T}{\partial \rho }\text{and} \\ \frac{d\rho }{dt}=-\frac{\partial H}{\partial \theta }=-\frac{\partial T}{\partial \theta }-\frac{\partial V}{\partial \theta }. \end{gathered}$$
采用所谓的跨越式积分器作为求解器。(iii)对于每一步，都会应用一个Metropolis验收标准来拒绝或接受样品(类似于MCMC)。不幸的是，HMC每次迭代都需要处理整个数据集，当数据集的大小增长到数百万甚至数十亿时，这在计算上是非常昂贵的。因此，许多现代算法都关注于如何以小批量的方式随机地执行计算。在此背景下，Welling和Teh首次提出将随机梯度下降(SGD)与langevin动力学(一种MCMC)相结合，以获得基于小批量SGD的MCMC算法的可扩展逼近。这项工作表明，在深度神经网络上执行贝叶斯推理可以像运行一个有噪声的SGD一样简单。该方法利用不包含HMC的动量项的一阶langevin动力学，开辟了随机梯度马尔可夫链蒙特卡洛(SG-MCMC)的研究新领域。
因此，可以采用几种扩展方法，包括使用二阶信息，如Fisher信息矩阵(FIM)， Hessian，自适应预处理对角矩阵，使用Fisher评分从非各向异性目标密度生成样本，以及使用一阶langevin动力学和Levy扩散噪声和动量在黎曼流形中生成样本。在这些方法中，所谓的参数依赖扩散矩阵被纳入，目的是抵消梯度的随机扰动。为此，提出了“恒温器”的思想，以便在参数相关的噪声中保持规定的恒定温度分布。Ahn等人为SG-MCMC设计了一个分布式计算系统，以利用现代计算例程，而Wang等人则表明，可以使用生成对抗模型(GANs)来提取样本以提高内存效率，而不是通过蒸馏来增强计算预测不确定性的运行时能力。最后，最近的其他趋势是减少随机梯度产生的方差和偏差的技术。
同时，SG-MCMC方法的理论和实践应用也有了长足的进步。Sato和Nakagawa首次证明了恒定步长SGLD算法弱收敛;Chen等研究了具有高阶积分器而非一阶欧拉积分器的SG-MCMC具有更快的收敛速度和更精确的不变测度，而Teh等研究了SGLD的一致性和波动性质。结果发现了该算法一致性的可验证条件是服从中心极限定理，以及发现了它的渐近偏差-方差分解如何依赖于步长序列。Nemeth和Fearnhead对SG-MCMC进行了更详细的综述，重点是支持理论结果。在实践中，SG-MCMC技术已被应用于形状分类和不确定性量化，根据经验研究验证了退火后验(或称为冷后验)的效果，并训练了深度神经网络以进行泛化和避免过拟合。

3)拉普拉斯近似: 拉普拉斯近似的目的是估计神经网络参数$p(\theta \mid x,y)$在一个多元正态分布的损失面局部模态周围的后验分布。在给定数据$(x,y)$的情况下，对MAP估计$\hat{\theta }$周围的权重进行对数后验的二阶泰勒级数展开，可以得到后验的拉普拉斯近似。如果我们假设高斯先验具有标量精度值$\tau >0$，那么这对应于常用的$L_2$-正则化，泰勒级数展开的结果为：
$$\begin{gathered} \log p(\theta \mid x,y)\approx \log p(\hat{\theta }\mid x,y) \\ +\frac{1}{2}(\theta -\hat{\theta }{)}^T(H+\tau I)(\theta -\hat{\theta }), \end{gathered}$$
这里一阶项消失了，因为log后的梯度$\delta \theta =\nabla \log p(\theta \mid x,y)$在最大$\hat{\theta }$处为零。两侧取指数，通过反向工程密度逼近积分，权重后验近似为均值为$\hat{\theta }$、协方差矩阵为$(H+\tau I{)}^{-1}$的高斯分布，其中$H$是$\log p(\theta \mid x,y)$的Hessian。这意味着模型的不确定性用Hessian $H$表示，结果是多元正态分布:
$$p(\theta \mid x,y)\sim \mathcal{N}\left(\hat{\theta },(H+\tau I{)}^{-1}\right).$$
与描述的其他两种方法相比，拉普拉斯近似可以应用于已经训练好的网络，并且通常适用于使用标准损失函数，如MSE或交叉熵和分段线性激活(如RELU)。Mackay和Denker等人在20世纪90年代率先提出了神经网络的拉普拉斯近似，一些现代方法为深度神经网络提供了扩展。

拉普拉斯近似的核心是Hessian估计。不幸的是，与Mackay和Denker等人提出的相对较小的网络相比，由于现代神经网络中的参数数量巨大，Hessian矩阵无法以一种可行的方式计算。因此，文献中提出了几种不同的近似H的方法。简要回顾如下。一些研究人员一直专注于包括非对角线元素，而不是对角线近似。其中，分层克罗内克因子(Kronecker Factor)近似阐述了显著的可扩展性。可以找到最近的一种扩展，重新缩放克罗内克因子矩阵的特征值，以便其特征基中的对角方差是准确的。这项工作提出了一个有趣的想法，人们可以证明，就Frobenius规范而言，所提出的近似更准确。然而，由于这种近似会受到特征向量估计不准确的影响，Lee等人提出进一步校正参数空间中的对角线元素。
现有的工作在保真-复杂性权衡中利用各种近似的Hessian获得拉普拉斯近似。在一些研究中，利用Fisher信息矩阵或高斯牛顿矩阵的对角线进行近似，从而得到独立分布的模型权值，以修剪权值或进行持续学习，以避免灾难性遗忘。Ritter等人将近似块对角Hessian的Kronecker分解应用于神经网络的可拓展拉普拉斯近似。这样，仍然假定不同层之间的权值是独立分布的，而不假定同一层之间的相关性。最近， 建立在当前对神经网络 损失景观(Hessian的许多特征值倾向于 为零)的理解的基础上，有工作开发了一种低秩近似， 导致层协方差矩阵的稀疏表示。此外，Lee等人证明 的拉普拉斯近似可以拓展到ImageNet大小的数据集和架构，并进一步表明，通过提出的稀疏化技术， 建模相关性的内存复杂度可以类似于对角线近似。最后，Kristiadi等人提出了一个简单的程序来计算最后一层高斯逼近(忽略所有其他神经网络层的模型不确定性)，并表明即使这样一个极简的解决方案也可以缓解ReLU网络的过度自信预测。最近的工作已经在hessian近似之外扩展了拉普拉斯近似 。为了解决广泛的众所周知的假设，即拉普拉斯近似是钟形真实后验，从而导致欠拟合行为，Humt等人提出使用贝叶斯优化，并表明拉普拉斯近似的超参数可以增加校准性能而有效地优化。该领域的另一项工作是Kristiadi等人，他们提出了不确定性单元——一种新的隐藏单元，可以改变损失景观的几何形状，从而可以进行更准确的推断。Shinde等人³论证了拉普拉斯近似在自动驾驶应用中的实际有效性，Feng等人则证明了在图像分类中(i)以半监督的方式合并上下文信息和(ii)领域自适应的可能性。这是通过在条件随机场内设计一元势实现的。也存在一些不需要多次前向传递来计算预测不确定性的实时方法。所谓线性化拉普拉斯近似利用Mackay的思想，并为分类任务用拉普拉斯桥进行扩展。在这个框架内，Daxberger等人提出通过推断子网络来增加协方差传播的表达力，同时保持计算可处理性。

4)贝叶斯方法总结: 深度学习的贝叶斯方法结合了深度神经网络的原理性贝叶斯学习，成为一个强有力的研究领域。对当前bnn的回顾主要集中在如何推断后验$p(\theta |x,y)$。据观察，最近的许多突破都是通过以小批量(随机)的方式执行近似贝叶斯推断，或研究相对简单但可拓展的技术(如MC-dropout或拉普拉斯近似)来实现的。因此，几项工作表明，现在可以在大规模环境下进行后验推断，而且自从bnn继先驱之后重新兴起以来，该领域已经有几种实用的逼近工具来计算更有表达力和更准确的后验。在精确推理技术之外的新领域也出现了挑战。一些例子是:(i)如何指定有意义的先验? (ii)如何有效地边缘化快速预测不确定性的参数? (iii)基础设施，如新的基准、评估协议和软件工具，以及(iv)更好地理解当前的方法及其潜在应用。

C. Ensemble Methods

1)原理: 集合根据来自多个所谓集合成员的预测得出一个预测。他们的目标是通过利用不同模型之间的协同效应来获得更好的泛化，认为一组决策者往往比单个决策者做出更好的决策。

对于一个集合 $f:X\to Y$ ，其中 $f_i:X\to Y$ for $i\in 1,2,...,M$, 这可以通过例如简单地平均成员的预测来实现,
$$f(x):=\frac{1}{M}\sum _{i=1}^M{f}_i(x).$$
基于这种直观的想法，在文献中可以找到一些将集成方法应用于不同类型的实际任务和方法的作品，如生物信息学、遥感或强化学习。除了精度的提高外，合集还通过评估成员预测的多样性，直观地表示模型对预测的不确定性。与贝叶斯方法和单一确定性网络方法相比，集成方法有两个主要的区别。
首先，集成背后的总体思路比较清晰，不同类型的集成方法的应用以及在不同领域的应用并没有太多突破性的差异。因此，本节重点讨论训练集合的不同策略，以及一些旨在使集合方法更有效的变化。
其次，最初没有引入集成方法来明确地处理和量化神经网络中的不确定性。虽然从集合预测推导出的不确定性是显而易见的，但由于它们实际上旨在减少模型的不确定性，所以集合是首先被引入和讨论以提高预测的准确性的。
因此，许多关于集成方法的工作并没有显式地考虑到不确定性。尽管如此，集合已经被发现很适合于神经网络中的不确定性估计

2)单模和多模估计: ensemble方法和其他方法的一个主要不同点就是它会考虑局部极小值的数目，也就分化成单模和多模估计。
为了产生协同效应并将单个成员的错误预测边缘化，在出现不确定结果的情况下，整体成员的行为必须有所不同。由神经网络定义的映射是高度非线性的，因此优化的损失函数包含许多训练算法可以收敛到的局部最优。确定性神经网络在解空间中收敛于一个局部最优。其他方法，如bnn，仍然收敛于一个单一最优，但额外考虑了该局部最优的不确定性。这意味着，在解周围的某个区域内的邻近点也会影响损失，也会影响测试样本的预测。由于这些方法关注的是单个区域，因此称为单模评估。与此相反，集成方法由多个网络组成，收敛于不同的局部最优。因此称为多模评估。

图7：确定性网络基于点估计学习参数，贝叶斯神经网络还考虑了单点周围的情况。确定性方法的集合基于点优化，但学习了几种不同的参数设置。

图7可视化了单模确定性、单模概率(贝叶斯)和多模集成方法考虑的参数。多模式评估的目标是不同的局部最优可能导致模型在预测中具有不同的优势和弱点，这样多个这样的模型的组合带来协同效应，从而提高整体性能。

3)将多样性带入ensembles: 应用ensemble方法的一个关键点是最大化单个网络之间行为的多样性。
为了增加多样性，可以采用几种不同的方法：

• 随机初始化和数据Shuffle
  由于损失是非常非线性的，神经网络的不同初始化通常会导致不同的训练结果。由于训练是在小批量上实现的，训练数据点的顺序也会影响最终的结果。
• Bagging and Boosting
  Bagging (Bootstrap aggregating)和Boosting是两种策略，通过从原始集合中采样新的训练样本集来改变使用的训练数据集的分布。Bagging是从训练数据中均匀抽样，并进行替换。通过替换过程，集成成员可以多次看到训练集中的单个样本，同时遗漏一些其他的训练样本。对于Boosting，成员被一个接一个地训练，并且在下一轮训练集迭代中被抽样的概率是基于已经训练好的集合的性能
• 数据增广
  对每个集成成员的输入数据进行随机扩充，会得到基于不同数据点训练的模型，因此通常会得到不同成员之间更大的多样性。
• 不同网络的集成
  不同网络结构的组合导致不同的损失景观，因此也可以增加结果预测的多样性。

在一些研究中，已经证明了由随机初始化引起的多样性是有效的，bagging甚至可能导致较弱的性能。Livieris等人评估了权重约束神经网络集成的不同bagging和Boosting策略。有趣的是，我们发现bagging对于一小部分成员表现更好，而boost对于大量成员表现更好。Nanni等人评估了生物图像分类任务中基于不同类型的图像增强的集成，并对它们进行了比较。Guo和Gould在一种集成方法中使用了增广方法进行目标检测。
两项工作都表明，使用增广的集合方法提高了结果的准确性。与此相反，在不确定度量化方面，指出图像增强会损害集成的校准，在使用集成方法时，后处理校准方法必须稍加调整。还介绍了其他针对特定任务诱导多样化的方法。例如，在2018年ECCV的一个方法中，为了专注于输入数据的不同部分，成员们使用了不同的注意力掩码训练。其他方法集中在训练过程并引入学习率调度器，旨在在一个训练过程中发现多个局部最优。接下来，可以根据一次训练中找到的局部最优值建立集合。值得注意的是，如果没有明确说明，迄今为止提出的工作和方法都是针对提高预测精度，而没有明确考虑不确定性量化。

4)不确定性量化: 除了提升准确，ensemble方法广泛用于建模复杂模型预测的不确定度，比如气候预测。
因此，合集也被用于量化深度神经网络预测的不确定性，在过去的几年里，它们变得越来越受欢迎. Lakshminarayanan等人的方法⁴经常被作为神经网络集成的不确定性估计的基础工作，并作为深度集成竞争力的参考.他们引入了一种集成训练流程来量化dnn中的预测不确定性。为了处理数据和模型的不确定性，成员网络设计了两个头，分别代表任务本身预测和对预测的数据不确定性的一个预测值。该方法是为分类和回归任务评估准确性，校准，和超出分布检测。在所有测试中，该方法的性能至少与用于比较的BNN方法，即蒙特卡洛Dropout和概率反向传播相同。Lakshminarayanan等人还表明，打乱训练数据和训练过程的随机初始化诱导了模型的足够多样性，以预测给定架构和数据集的不确定性。有研究发现bagging降低了集成方法对调研任务的预测精度。Gustafsson等人⁵介绍了一个框架，用于比较不确定性量化方法，并特别关注现实生活中的应用。在这个框架下，他们比较了集成和蒙特卡洛dropout，发现集成更可靠，更适用于现实生活中的应用。这些发现支持了Beluch等人报告的结果，他们发现集成方法比蒙特卡洛Dropout方法对主动学习任务提供更准确和更好的校准预测。Ovadia等人基于受分布偏移影响的测试集评估了不同的不确定度量化方法。过度评价包含多种模型类型和数据形式。作为一个结论，作者指出，对于5个相对较小的集合规模，深度集合似乎表现最好，比与之比较的方法对数据集迁移更稳健。Vyas等人提出了一种改进的非分布样本检测的集合方法。对于每个成员，训练数据的一个子集被认为是分布外的。在训练过程中，引入了一种损失，即在域内和分布外子集的平均熵之间寻找一个大于零的最小余量，从而显著改善了分布外检测。

5)使ensemble方法更有效: 和单模型方法相比，ensemble方法会带来显著地计算开销和内存开销。
在为实际应用程序部署集成时，可用内存和计算能力通常是有限的。这些限制很容易成为瓶颈，并对反应时间有限的应用至关重要。减少模型的数量可以减少内存和计算功耗。一些剪枝方法通过对成员进行剪枝和减少成员之间的冗余来降低集合的复杂性。并开发了几种基于不同多样性度量的方法，在不严重影响性能的情况下去除单个成员。

蒸馏是另一种方法，其网络的数量减少到一个单一的模型。这是一个教会单个网络表示一组神经网络知识的过程。第一个对神经网络蒸馏的研究是在部署大规模分类问题时资源受到了限制。该方法将原始分类问题分解为多个子问题，这些子问题集中在难以区分的单个类块上。几个较小的训练器网络在子问题上训练，然后教一个学生网络在同一时间分离所有类别。与此相反，集成蒸馏方法通过单个网络捕获集成的行为。第一个集成蒸馏的工作使用集成成员的平均softmax输出，以教导一个学生网络导出的预测不确定性。Englesson和Azizpour证明了这种方法产生的预测分布结果，另外还讨论了分布外样本的处理。当对成员的输出取平均值时，模型的不确定性就会丢失，而这种不确定性体现在各种集成输出中。为了克服这个缺点，研究人员应用了学习高阶分布的思想，即分布上的分布，而不是直接预测输出。然后根据与平均分布的散度提取成员。这一想法与先验网络和证据神经网络密切相关，在单个确定性方法那节中描述。还有方法将集合成员建模，并将其提炼为预测狄利克雷分布参数的先验网络。然后最小化集合成员的平均狄利克雷分布和蒸馏网络输出之间的KL散度。Lindqvist等人将这一思想推广到任何其他可参数化分布。因此，该方法也适用于回归问题，例如通过预测平均值和标准差来描述一个正态分布。在几次测试中，由这些方法生成的蒸馏模型能够区分数据不确定性和模型不确定性。虽然蒸馏方法不能完全捕获隐含的集成行为，但它已经表明，它们能够提供良好的，对一些实验甚至可比较的结果。

其他方法，如sub-ensembles 和 batch-ensembles，通过在单个成员之间共享部分来减少计算工作量和内存消耗。重要的是要注意，当集成的部分被共享时，集成成员使用不同模型架构的可能性可能会消失。另外，模型的训练不能完全独立运行。因此，实际训练所需的时间并不一定会像计算工作量那样减少。sub-ensembles将神经网络体系结构分为两个子网络。主干网络用于从输入的数据中提取一般信息，而任务网络则利用这些信息来完成实际任务。为了训练sub-ensemble，首先根据单个模型训练过程得到的参数确定每个成员主干网络的权重;然后，对每个成员的任务网络参数进行独立训练。因此， 成员是用一个公共主干和一个单独的任务子网构建的。由于干线网络的训练和评估必须只做一次，训练和测试所需的计算的数量减少了因子 $\frac{M\cdot N_{\text{task}}+N_{\text{trunk}}}{M\cdot N}$, 其中 $N_{\text{task}}$, $N_{\text{trunk}}$, 和 $N$表示任务网络、主干网络和完整网络中的变量数量。Valdenegro-Toro进一步强调了共享主干网络的使用，认为主干网络在一般计算上比任务网络更昂贵。与此相反，batch-ensembles在每一层将成员网络彼此连接起来。集成成员的权重描述为一个共享权重矩阵$W\in {\mathbb{R}}^{n\times m}$ 和 $M$ 个独立秩一矩阵$F_i\in {\mathbb{R}}^{n\times m}$的 Hadamard乘积。秩一矩阵能够写成两个向量$s\in {\mathbb{R}}^n$ 和 $r\in {\mathbb{R}}^m$ 的乘积 $F_i=r_i{s}_i^{\text{T}}$ ， 因此矩阵 $F_i$ 能够被 $n+m$ 个参数描述. 在这种方法中，每增加一个集成成员，参数的数量就会增加 $\frac{n+m}{M\cdot (n+m)+n\cdot m}+1$ 而不是 $\frac{M+1}{M}=1+\frac{1}{M}$。一方面，使用这种方法，成员不再是独立的，所有成员都必须并行训练。另一方面，作者还表明并行化可以实现类似于在小批量和单个单元上的优化。

6)ensemble方法总结: ensemble方法很容易应用，因为没有对单个确定性模型的复杂实现或大的修改。而且ensemble成员之间可以独立训练，和容易并行。训练的ensembles也很容易简单拓展，但是所需的计算开销和内存开销是随着训练和估计的ensemble 成员数目线性增长的。
使用集成方法的主要挑战是需要在集成成员中引入多样性。对于准确性、不确定性量化和分布外检测，随机初始化、数据变换和增强已被发现足以满足许多应用和任务。因为无论如何都可以应用这些方法，所以它们不需要太多额外的工作。单个集成成员的独立性导致每增加一个成员所需的内存和计算能力的线性增加。这对训练和测试都适用。这限制了集成方法在许多实际应用中的部署，在这些实际应用中，计算能力或内存有限，应用是时间关键的，或包含有高推断时间的非常大的网络。
集成方法的许多方面只研究了预测精度的性能，而没有考虑预测的不确定性。这也适用于对广泛的问题和数据集的不同训练策略的比较。特别是由于单个成员的过度自信可以转移到整个集合中，鼓励成员做出不同的错误预测而不是所有成员做出相同的错误预测的策略需要进一步研究。为了更好地理解群落行为，Fort等人⁶对损失景观的进一步评估 可以提供有趣的见解。

D. Test Time Augmentation

受到ensemble方法和对抗样本的启发，test time data augmentation是更简单的预测不确定性估计的技术之一。其基本方法是对每个测试样本应用数据增强技术创建多个测试样本，然后对所有这些样本进行测试，计算一个预测分布，以测量不确定性。这种方法背后的想法是，扩大的测试样本允许探索不同的视角，因此能够捕捉不确定性。这种测试时间数据增强技术主要用于医学图像处理。其中一个原因是医学图像处理领域在使用深度学习时已经大量使用了数据增强，因此在测试期间只使用相同的数据增强来计算不确定性是非常容易的。另一个原因是，收集医学图像的成本很高，因此迫使从业者依赖于数据增强技术。Moshkov等人将测试时增强技术用于细胞分割任务。为此，他们在将测试数据输入经过训练的UNet或Mask R-CNN架构之前创建了多个变体。随后，他们使用多数投票来创建最终输出的分割掩码，并讨论了应用不同增强技术的策略，以及它们如何影响深度网络的最终预测结果。

总的来说，测试时增强是一种估计不确定性的简单方法，因为它保持底层模型不变，不需要额外的数据，并且很容易使用现成的库将其付诸实践。尽管如此，需要记住的是，在应用这种技术时，应该只对数据应用有效的增广，这意味着增广不应该从目标分布外部生成数据。由于问题的性质、训练数据的大小、深度神经网络结构和增强的类型等多种因素，测试时间增强可以将许多正确的预测变成不正确的预测(反之亦然)。为了限制这些因素的影响，Shanmugam等人提出了一种考虑了这些因素的基于学习的测试时增强方法。特别地，该方法学习了一个函数，该函数从测试样本的每个增强中聚合预测。与该方法相似，Molchanov等人提出了一种名为“贪婪策略搜索”的方法，通过选择包含在固定长度策略中的增强来构造一个测试时增长策略。类似地，Kim等人提出了一种从训练数据学习损失预测器的方法，用于实例感知测试时增强选择。预测器为给定的样本选择具有最低预测损失的测试时增强。

虽然可学习的测试时间增强技术有助于选择有效的增强，但主要的开放问题之一是找出不同类型的增强对不确定性的影响。例如，反射等简单的增强不能捕捉到很多不确定性，而一些领域专门的拉伸和剪切捕捉到更多的不确定性。同样重要的是，找出需要多少增强才能正确地量化给定任务中的不确定性。这在地球观测等应用中尤其重要，因为在有限的资源下，可能需要在全球范围内进行推断。

E. Neural Network Uncertainty Quantification Approaches for Real Life Applications

为了在现实生活任务中使用所提出的方法，必须考虑几个不同的因素。内存和计算能力经常受到限制，而现实世界中的许多任务都是时间紧迫的。表1给出了主要属性的概述。所提供的应用都有其优点和缺点，这取决于用户感兴趣的属性。集成方法和测试时间增广方法相对容易应用，而贝叶斯方法对模型参数的不确定性给出了清晰的描述，也提供了更深入的理论基础。计算工作量和内存消耗是现实应用中常见的限制，其中单一确定性网络方法性能最好，但也可以考虑集成的蒸馏或有效的贝叶斯方法。在不同类型的贝叶斯方法中，性能、计算工作量和实现工作量仍然存在很大差异。拉普拉斯近似比较容易应用，与抽样方法相比，需要的计算工作量要少得多。此外，通常已经存在针对某个应用的预训练网络。在这种情况下，拉普拉斯近似和外部确定性单网络方法一般可以应用于已经训练好的网络。

在实际应用中对不确定性进行量化时必须考虑到的另一个重要方面是不确定性的来源和类型。对于现实生活中的应用程序，为了避免网络的意外决策并意识到对抗性攻击，分布外检测形成了可能是最重要的挑战。特别是由于不确定性量化的许多动机是由风险最小化给出的，提供风险规避预测的方法是一个重要的评估领域。许多工作已经展示了在多个任务中检测分布外样本的能力，并为实际应用程序的部署构建了一个强大的基础工具集。然而，在现实生活中，任务比在数据集(例如，MNIST或CIFAR数据集等)中寻找非分布样本要困难得多，主要的挑战在于在几个现实世界的数据集上相互比较这些方法。Gustafsson等人的工作⁵为评估更适合实际应用需求的方法迈出了重要的第一步。有趣的是，他们发现他们的测试集合优于贝叶斯方法。这表明，由集成给出的多模评价在实际应用中具有很强的实用性。尽管如此，贝叶斯方法也带来了强大的结果，而且还带来了强大的理论基础。作为一种方法，有效的集合策略和贝叶斯方法的组合可以结合模型参数的可变性，同时仍然考虑几种模式来进行预测。此外，单一确定性方法作为先验网络提供了可比较的结果，同时大大减少了计算能力。然而，这种效率常常伴随着一个问题，即必须为训练过程提供分布内和分布外的样本集。一般来说，新问题和损失公式的发展，会导致潜在问题更好的理解和描述，并形成一个重要的研究领域。

上一篇：深度神经网络的不确定性（上）

下一篇：深度神经网络的不确定性（下）

---

1. “The aleatoric uncertainty estimation using a separate formulation with virtual residuals”.ICPR2021. ↩︎

2. “Hybrid monte carlo”.Physics letters 1987. ↩︎

3. “Learning multiplicative interactions with bayesian neural networks for visualinertial odometry”.ICML2020 workshop ↩︎

4. “Simple and scalable predictive uncertainty estimation using deep ensembles". nips 2017 ↩︎

5. “Evaluating scalable bayesian deep learning methods for robust computer vision”.cvpr2020 workshop ↩︎ ↩︎

6. “Deep ensembles: A loss landscape perspective”.arXiv preprint arXiv:1912.02757, 2019 ↩︎