【插值与拟合】黄河小浪底调水调沙问题

插值

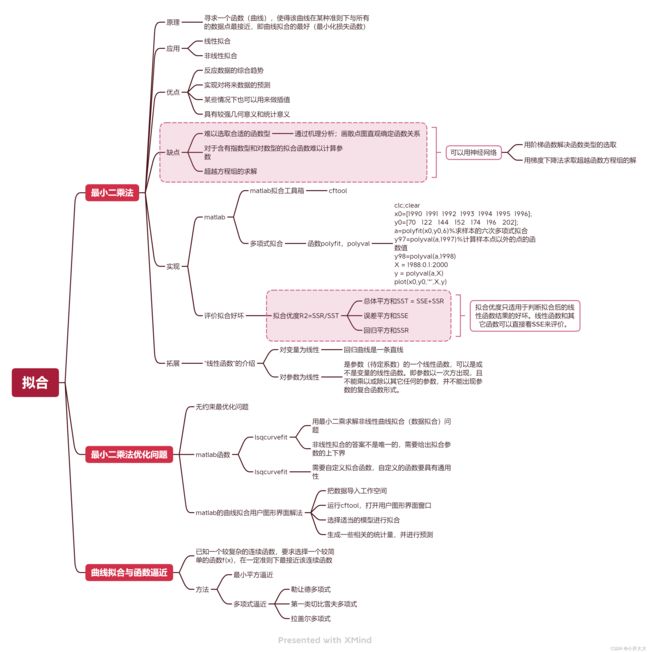
拟合

案例——黄河小浪底调水调沙问题

问题重述

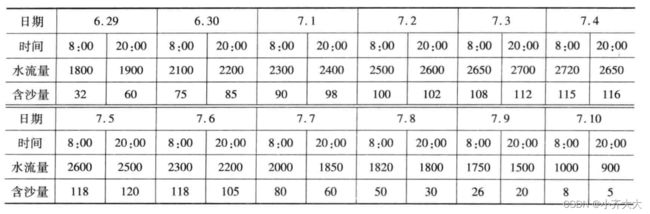
2004年6月至7月黄河进行了第三次调水调沙试验,特别是首次由小浪底、三门峡和万家寨三大水库联合调度,采用接力式防洪预泄放水,形成人造洪峰进行调沙试验获得成功。这次调水调沙试验一个重要目的就是由小浪底上游的三门峡和万家寨水库泄洪,在小浪底形成人造洪峰,冲刷小浪底库区沉积的泥沙,在小浪底水库开闸泄洪以后,从6月27日开始三门峡水库和万家寨水库陆续开闸放水,人造洪峰于6月29日先后到达小浪底,7月3日达到最大流量2700$m^3$/s,使小浪底水库的排沙量也不断地增加。由小浪底观测站从6月29日到7月10日检测到的试验数据如下：

现在,根据试验数据建立数学模型研究下面的问题:

(1）给出估计任意时刻的排沙量及总排沙量的方法。

(2）确定排沙量与水流量的关系。

模型的建立与求解

数据的量化与处理

观察数据可以发现给定的观测时刻间距固定为12h，以6月29日00:00开始计时，则各次观测时刻相对于开始时刻的量化为
$$t_i=3600(12i-4),i=1,2,...,24$$
式中：单位为s，i表示观测序次。

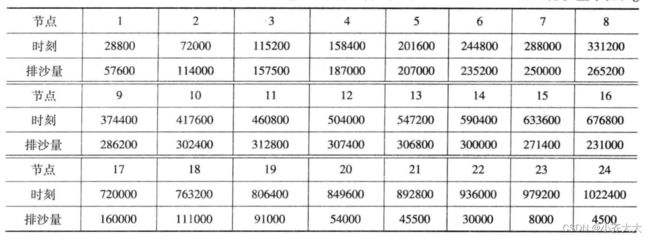
记第i次观测时水流量为$v_i$，含沙量为$c_i$，则第i次观测时的排沙量为$y_i=c_i{v}_i$。整理后的插值条件如表所示：

插值与拟合

问题一

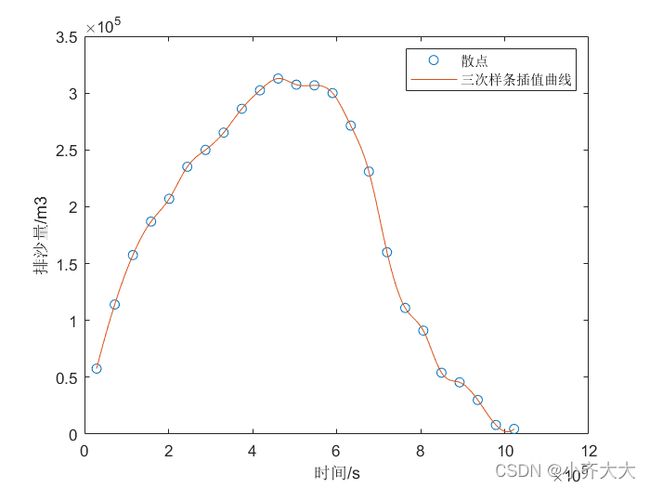
对于问题（1），根据所给问题的试验数据，要估计出任意时刻的排沙量，就需要找到时间和排沙量的函数关系，可以通过现有的样本点构造插值函数，这样任意时刻的排沙量就可以通过对应时刻的插值函数值来确定。考虑到实际当中的排沙量应该是时间的连续函数，这对插值函数的光滑性具有较高的要求，为了使得插值函数具有较高的光滑性和连续的曲率，提高插值函数的精度，本文采用三次样条函数进行插值，这样便可以直接用积分计算任意时刻的总排沙量。

利用matlab，求出三次样条插值函数，得到排沙量y=y(t)与时间t的关系，然后依据插值函数对时间进行积分，就可以得到总的排沙量
$$z={\int }_{t1}^{ti}y(t)dt$$
最后求得总的排沙量为$1.844\ast 10^{9}t$，matlab代码如下：

clc,clear
load data3.txt  %把观测表中的日期和时间数据行删除，余下的数据保存在纯文本文件
liu=data3([1,3],:); liu=liu'; liu=liu(:);  %提出水流量并按照顺序变成列向量
sha=data3([2,4],:); sha=sha'; sha=sha(:); %提出含沙量并按照顺序变成列向量
y=sha.*liu; y=y';  %计算排沙量，并变成行向量
i=1:24;%观测序次
t=(12*i-4)*3600;%观测时间
t1=t(1);t2=t(end);
pp=csape(t,y); %进行三次样条插值
xsh=pp.coefs  %求得插值多项式的系数矩阵，每一行是一个区间上多项式的系数。
TL=quadl(@(tt)fnval(pp,tt),t1,t2)   %求总含沙量的积分运算

%%%画个图
T=28800:0.1:1022400;
my=fnval(pp,T);
plot(t,y,'o',T,my);%三次样条插值曲线以及原数据散点图

问题二

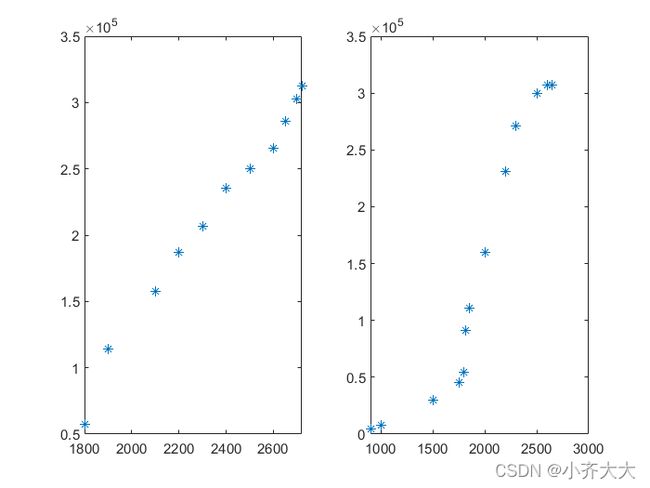
对于问题（2），研究排沙量与水流量的关系，从实验数据以及散点图可以看出，开始排沙量是随着水流量的增加而增长，而后是随着水流量的减少而减少。显然，变化规律是非线性的，为此，把问题分为两个部分，从开始水流量增加到最大值2720这一增长过程为第一阶段，从水流量的最大值到结束为第二阶段，分别研究水流量与排沙量的关系。

从散点图可以看出，第一阶段基本上是线性关系。为了提高模型的精度，第一阶段和第二阶段都准备用一次和二次曲线来拟合，哪一个模型的剩余标准差较小就选之。

最后求得第一阶段排沙量y与水流量v之间的拟合方程为一个一次多项式：
$$y=250.5655v-373384.4661$$
第二阶段的拟合方程为一个二次多项式，即：
$$y=0.1067v_2-180.4668v+72421.0982$$
matlab代码如下：

clc,clear
load data3.txt  %把表5.8中的日期和时间数据行删除，余下的数据保存在纯文本文件
liu=data3([1,3],:); liu=liu'; liu=liu(:);  %提出水流量并按照顺序变成列向量
sha=data3([2,4],:); sha=sha'; sha=sha(:); %提出含沙量并按照顺序变成列向量
y=sha.*liu;   %计算排沙量，这里是列向量
format long e 
%以下是第一阶段的拟合
for j=1:2
nihe1{j}=polyfit(liu(1:11),y(1:11),j);%拟合多项式，系数排列从高次幂到低次幂
yhat1{j}=polyval(nihe1{j},liu(1:11));  %求预测值
%以下求误差平方和与剩余标准差
cha1(j)=sum((y(1:11)-yhat1{j}).^2); rmse1(j)=sqrt(cha1(j)/(10-j));
end
celldisp(nihe1)  %显示细胞数组的所有元素
rmse1
%以下是第二阶段的拟合
for j=1:2
    nihe2{j}=polyfit(liu(12:24),y(12:24),j); %这里使用细胞数组
    yhat2{j}=polyval(nihe2{j},liu(12:24)); 
    rmse2(j)=sqrt(sum((y(12:24)-yhat2{j}).^2)/(12-j)); %求剩余标准差
end
celldisp(nihe2)  %显示细胞数组的所有元素
rmse2
format  %恢复默认的短小数的显示格式