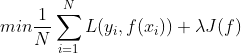《统计学习方法》(李航)：模型评估选择、正则化与交叉验证、泛化能力、生成模型与判别模型、监督学习应用

PS：所写内容为读书笔记，如需了解更详细内容请购买正版书籍

1.4  模型评估与选择

1.4.1  训练误差和测试误差

训练误差：模型对训练集预测结果的误差

测试误差：模型对测试集测试结果的误差

1.4.2  过拟合与模型选择

过拟合（over-fitting）：学习时选择的模型所包含的参数过多，以至于出现这一模型对已知数据预测很好，但对未知数据预测很差的现象。

当模型的复杂度增大时，训练误差会逐渐减小并趋近于0，而测试误差会先减小后增大。当选择的模型参数复杂度过高时，模型往往太过于“依赖”训练数据。所以在学习中，需要选择复杂度适当的模型。有两种常用的方法：正则化与交叉验证。

1.5  正则化与交叉验证

1.5.1  正则化

模型选择的典型方法是正则化（regulation），正则化是结构风险最小化策略的实现，是在经验风险上加上一个正则化项（regularizer）或惩罚项（penalty term）。正则化项一般是模型复杂度的单调递增函数，模型越复杂，正则化值越大。比如，正则化项可以是模型参数向量的范数。

正则化项一般具有如下形式：

其中，第1项是经验风险，第2项是正则化项，为调整系数。

1.5.2  交叉验证

如果给定的样本数据充足，进行模型选择的一种简单方法是随机的将数据集切分成三部分，分别为训练集（trainging set）、验证集（validation set）和测试集（test set）。训练集用来训练模型，验证集用于模型选择，测试集用于模型的选择。

1.  简单交叉验证

首先随机将训练数据分为两部分，一部分作为训练集，另一部分作为验证集（例如，70%的数据为训练集，30%的数据为测试集）；每次训练时拿训练集训练，验证集验证，选择验证集上误差最小的模型参数。

2.S折交叉验证

首先将已给训练数据分为S个互不相交、大小相同的子集，然后利用S-1个子集的数据训练模型，余下的子集验证模型。这一过程重复进行，选择最优模型参数。

1.6  泛化能力

1.6.1  泛化误差

学习方法的泛化能力是指由该方法学习到的模型对未知数据的预测能力。实际中采用最多的方法是利用测试集的误差来评价学习方法的泛化能力，这种评价是依赖于测试集的。

泛化误差就是学习到的模型对于未知数据的误差，泛化误差越小，泛化能力越强，模型对未知数据的效果越好。

1.6.2  泛化误差上界

一个学习方法会有泛化误差上界，通过比较不同学习方法的泛化误差上界可以比较不同学习方法的泛化能力。

二分类问题的泛化误差上界：

定理1.1（二分类问题的泛化误差上界）对于二分类问题，当假设空间是有限个函数的集合时，对任意一个函数，至少以概率，以下不等式成立：

其中：

不等式左边R(f)是泛化误差，右边为泛化误差上界。在泛化误差上界中，第一项为训练误差，训练误差越小，泛化误差越小；第二项为N的单调递减函数，当N趋近于无穷时趋近于0；同时也是阶的函数，假设空间包含的函数越多，其值越大。

1.7  生成模型与判别模型

监督学习方法又可分为生成方法与判别方法。所学到的模型分别称为生成模型与判别模型。

生成方法由数据学习联合概率分布P(X,Y)，然后求出条件概率分布P(Y|X)作为预测的模型，即生成模型：

这样的方法之所以称为生成方法是因为模型表示了给定输入X产生输出Y的生成关系。典型的生成模型有朴素贝叶斯法和隐马尔科夫模型。

判别方法由数据直接学习决策函数或者条件概率分布，判别方法关心的是对给定的输入X，应该预测什么样的输出Y。典型的判别模型有：k近邻法、感知机、决策树、逻辑斯蒂回归模型、最大熵、支持向量机、提升方法和条件随机场。

1.8  监督学习应用

1.8.1  分类问题(classification)

分类是监督学习的一个核心问题。在监督学习中，当输出变量Y取值为有限个离散值时，预测问题就变成了分类问题。此时输入X既可以是离散也可以是连续的。监督学习从数据中学习一个分类模型，称为分类器（classifier）。分类的类别为多个时，称为多分类问题。

评价分类器的指标有准确率、精确率和召回率。

根据分类情况会有四种情况：

TP：（true-positive）——将正类预测为正类的个数。

FN：（false-positive）——将正类预测为负类的个数。

FP：（false-positive）——将负类预测为正类的个数。

TN：（true-negtive）——将负类预测为负类的个数。

精确率（所有预测结果为正类的个数中，预测正确的比例）：

召回率（所以正类样本的预测结果中，预测正确的比例）：

此外还有值，是精确率和召回率的调和均值：，即

1.8.2  标注问题(tagging)

可以认为标注问题是分类问题的一个推广。标注问题的输入是一个观测序列，输出是一个标记序列或状态序列。

1.8.3  回归问题(regression)

回归是监督学习的另一个重要问题。回归用于预测输入变量（自变量）和输出变量（因变量）之间的关系，特别是当输入变量的值发生变化时，输出变量的值随之发生的变化。回归模型正是表示从输入变量到输出变量之间映射的函数。回归问题的学习等价于函数拟合：选择一条函数曲线使其很好地拟合已知数据且很好地预测未知数据。

回归问题按照输入变量的个数，分为一元回归和多元回归；按照输入变量和输出变量之间关系的类型及模型的类型，分为线性回归和非线性回归。