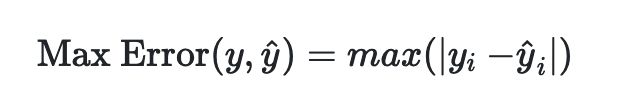机器学习——Sklearn学习笔记(2)模型选择和评估
Sklearn学习笔记(2)模型选择和评估
- 写在前面
-
- 机器学习流程
- 基本概念
- 1. 交叉验证:评估评估器的性能
-
- 1.1 交叉验证的指标
-
- 1.1.1 cross_val_score():最容易
- 1.1.2 cross_validate():多指标
- 1.1.3 通过交叉验证获取预测结果
- 1.2 其它交叉验证方法:在cross_validation 模块中(以迭代器的形式)
-
- 1.2.1 Kfold()
- 1.2.2 RepeatedKFold()
- 1.2.3 LeaveOneOut()
- 1.2.4 LeavePOut()
- 1.2.5 ShuffleSplit()
- 接下来的是另一类方法(变种):基于类标签、具有分层的交叉验证迭代器
- 1.2.6 StratifiedKFold (分层 K折)
- 1.2.7 ShuffleSplit (分层随机)
- 基于这类方法的用于分组数据的交叉验证迭代器
- 暂略
- 1.3 关于shuffling的一点说明
- 1.4 交叉验证模型选择
- 2. 调整评估器的超参数
-
- 2.1 GridSearchCV():穷尽的网格搜索
- 2.2 RandomizedSearchCV(): 随机参数优化
- 2.3 参数搜索技巧
-
- 指定目标指标(metric)
- 为评估指定多个指标
- 综合评估和参数空间
- 模型选择:开发和评估
- 并行机制
- 对故障的鲁棒性
- 2.4 暴力参数搜索的替代
-
- 模型特定交叉验证
- 信息标准
- 出袋估计
- 3. 指标和评分:量化预测的质量
-
- 3.1 不同评分方法的scoring参数
-
- 3.1.1 常见场景: 预定义值
- 3.1.2 定义自己的评分策略
- 3.1.3 定义自己的评分模块
- 3.1.4 使用多个指标
- 3.2 分类指标
-
- 3.2.1 从二分到多分类和 multilabel
- 3.2.2 精确度得分
- 3.2.3 平衡的准确度评分
- 3.2.4 Cohen’s kappa
- 3.2.5 混淆矩阵
- 3.2.6 分类报告
- 3.2.7 Hamming loss (汉明损失)
- 3.2.8 Precision, recall and F-measures(精确率、召回率、F 值-度量)
-
- 3.2.8.1 二分类
- 3.2.8.2 多分类和多标签分类
- 3.2.9Jaccard 相似性系数分数
- 3.2.10 Hinge 损失
- 3.2.11 Log 损失
- 3.2.12 Matthews 相关系数
- 3.2.13 多标签混合矩阵
- 3.2.14 受试者工作特性曲线 (ROC)
- 3.2.15 零一损失
- 3.2.16 Brier 分数损失
- 3.3 多标签排序指标
- 3.4 回归指标
-
- 3.4.1 解释方差得分
- 3.4.2 最大误差
- 3.4.3 平均绝对值
- 3.4.4 均方误差
- 3.4.5 均方误差对数
- 3.4.6 中位绝对误差
- R² score, 可决系数
- 聚类指标
- 虚拟估计: DummyClassifier()
- 4. 模型持久化
- 5. 验证曲线:绘制分数图来评估模型
-
- 5.1 验证曲线(validation curve)
- 5.2 学习曲线
- 写在后面
写在前面
心得:先明白框架和基概念,不然容易迷糊和迷路。
机器学习流程
有监督机器学习的基本步骤:
导入模型 (选择模型)
|
初始化模型 (选择模型超参数)
|
拟合数据( 用模型拟合训练数据)——模型验证(cv)
|
预测数据(用模型预测新数据的标签)
前两个是最重要的。
基本概念
- 预测
机器学习的任务分为两大类:
分类——预测离散标签
回归——预测连续标签
所以,不管是分类还是回归,预测就是机器学习的任务。
后面会知道,针对分类任务的机器学习模型叫做 classifier,针对回归任务的机器学习模型叫做 estimator。
-
评估器(estimator)
-
模型(model)
-
拟合
-
模型训练
-
转换器
- estimator、classiifier、predictor、model 傻傻分不清?
an estimator is a predictor found from regression algorithm.
a classifier is a predictor found from a classification algorithm.
a model can be both an estimator or a classifier.
一句话:estimator、classiifier 本质上都是预测器(predictor);模型可以是 estimator 或者classiifier 。
- transformer 和 estimator ?
Transformer transforms the input data (X) in some ways.
Estimator predicts a new value (or values) (y) by using the input data (X).
transform() 用于转换数据X,理解为输如X1,输出X2;
estimator 用于模型预测,理解为输入X 输出 y;
当然它们都有一个拟合函数 fit(),用于输出之前的训练。
-
超参数
模型初始化时,人为选择和输入的参数。 -
模型初始化
(模型训练之前)模型超参数的选择过程 -
模型验证(model validation)
(模型训练之后)评估模型性能的过程 -
方差
-
偏差
方差和偏差是验证模型泛化误差常用的两个指标。
估计值的偏差是不同训练集的平均误差。估计值的方差用来表示它对训练集的变化有多敏感。
1. 交叉验证:评估评估器的性能
-
模型验证(validation)
上面也说到了,是模型训练之后,评估模型性能的一个过程。 -
实验方法 1. 训练和测试是同一套数据集(数据集 = 训练集 = 测试集)——导致过拟合
将在数据集 D 中训练得到的模型 M 应用在数据集 D上进行测试。(这是错误做法,会导致模型”过拟合“:在训练集上表现良好,在未知数据集上表现很差)
-
改进方法:划分测试集
将原数据集一分为二,分为训练集和测试集分别用于模型训练和模型测试;
(可以通过**网格搜索(grid search)**的方式确定模型最优参数) -
实现
划分数据集:train_test_split() -
实验方法 2:数据集 = 训练集 + 测试集——有过拟合风险
原因:因为模型是根据训练集数据来进行参数优化的,这避也很容易导致模型在“未知”数据(测试集或全新的数据集)上表现不理想(过拟合)
-
改进方法:划分验证集
将原数据集一分为三,即 数据集 = 训练集 + 验证集 + 测试集 -
方法2的一个问题:可用于模型学习的数量减少(模型失去了一部分训练机会)
-
解决:使用交叉验证
交叉验证最基本的方法被称之为 k-折交叉验证,其他方法会在下面描述,主要原则基本相同 。
k-折交叉验证过程:1.将训练集划分为 k 个较小的集合
2.将 k-1 份训练集子集作为 training data (训练集)训练模型;
3.将剩余的 1 份训练集子集用于模型验证(也就是把它当做一个测试集来计算模型的性能指标,例如准确率)。
4.每一个 k 折重复2、3操作
k-折交叉验证得出的性能指标是循环计算中每个值的平均值。 该方法虽然计算代价很高,但是它不会浪费太多的数据(如固定任意测试集的情况一样), 在处理样本数据集较少的问题(例如,逆向推理)时比较有优势。

1.1 交叉验证的指标
使用交叉验证最简单的方法是在估计器和数据集上调用 cross_val_score 辅助函数。
1.1.1 cross_val_score():最容易
- 例子:
>>> from sklearn.model_selection import cross_val_score
>>> clf = svm.SVC(kernel='linear', C=1)
>>> scores = cross_val_score(clf, iris.data, iris.target, cv=5)
>>> scores
array([0.96..., 1. ..., 0.96..., 0.96..., 1. ])
- 打印平均值和 95%的置信区间:
>>> print("Accuracy: %0.2f (+/- %0.2f)" % (scores.mean(), scores.std() * 2))
Accuracy: 0.98 (+/- 0.03)
可以通过 scoring 参数改变评估器的 score()方法:
>>> from sklearn import metrics
>>> scores = cross_val_score(
... clf, X, y, cv=5, scoring='f1_macro')
>>> scores
array([0.96..., 1. ..., 0.96..., 0.96..., 1. ])
- 交叉验证参数
当 cv 参数是一个整数时, cross_val_score 默认使用 KFold 或 StratifiedKFold 策略,后者会在估计器派生自 ClassifierMixin 时使用。
也可以通过迭代,传入选择其它参数:
>>> from sklearn.model_selection import ShuffleSplit
>>> n_samples = X.shape[0]
>>> cv = ShuffleSplit(n_splits=5, test_size=0.3, random_state=0)
>>> cross_val_score(clf, X, y, cv=cv)
array([0.977..., 0.977..., 1. ..., 0.955..., 1. ])
1.1.2 cross_validate():多指标
cross_validate ()与 cross_val_score ()在两个地方有不同:
- 它允许指定多个指标进行评估.
- 除了测试得分,它还会返回一个包含训练得分、拟合次数和 score-times (得分次数)的一个字典。
例子:
使用多个评价指标:
>>> from sklearn.model_selection import cross_validate
>>> from sklearn.metrics import recall_score
>>> scoring = ['precision_macro', 'recall_macro']
>>> clf = svm.SVC(kernel='linear', C=1, random_state=0)
>>> scores = cross_validate(clf, X, y, scoring=scoring)
>>> sorted(scores.keys())
['fit_time', 'score_time', 'test_precision_macro', 'test_recall_macro']
>>> scores['test_recall_macro']
array([0.96..., 1. ..., 0.96..., 0.96..., 1. ])
也可以使用字典映射:
>>> from sklearn.metrics import make_scorer
>>> scoring = {'prec_macro': 'precision_macro',
... 'rec_macro': make_scorer(recall_score, average='macro')}
>>> scores = cross_validate(clf, X, y, scoring=scoring,
... cv=5, return_train_score=True)
>>> sorted(scores.keys())
['fit_time', 'score_time', 'test_prec_macro', 'test_rec_macro',
'train_prec_macro', 'train_rec_macro']
>>> scores['train_rec_macro']
使用单个指标:
>>> scores = cross_validate(clf, X, y,
... scoring='precision_macro', cv=5,
... return_estimator=True)
>>> sorted(scores.keys())
['estimator', 'fit_time', 'score_time', 'test_score']
1.1.3 通过交叉验证获取预测结果
corss_val_predict() 和 cross_val_score():
除了返回结果不同,函数 cross_val_predict 具有和 cross_val_score 相同的接口。
注意:
cross_val_predict函数的结果可能会与cross_val_score函数的结果不一样,因为在这两种方法中元素的分组方式不一样。函数cross_val_score在所有交叉验证的折子上取平均。但是,函数cross_val_predict只是简单的返回由若干不同模型预测出的标签或概率。因此,cross_val_predict不是一种适当的泛化错误的度量。
cross_val_predict() 比较适合做的:
- 从不同模型获得的预测结果的可视化。
- 模型混合: 在集成方法中,当一个有监督估计量的预测被用来训练另一个估计量时
1.2 其它交叉验证方法:在cross_validation 模块中(以迭代器的形式)
这部分讲的主要是除了K-fold之外的其它交叉验证的方法,比如 Leave One Out(留一法)等等。
1.2.1 Kfold()
KFold 的 k = n, 就是 Leave One Out(留一法)。预测函数学习时使用 k - 1 个折叠中的数据,最后一个剩下的折叠会用于测试。
例子:
>>> import numpy as np
>>> from sklearn.model_selection import KFold
>>> X = ["a", "b", "c", "d"]
>>> kf = KFold(n_splits=2)
>>> for train, test in kf.split(X):
... print("%s %s" % (train, test))
[2 3] [0 1]
[0 1] [2 3]
1.2.2 RepeatedKFold()
重复 Kfold n 次。
>>> import numpy as np
>>> from sklearn.model_selection import RepeatedKFold
>>> X = np.array([[1, 2], [3, 4], [1, 2], [3, 4]])
>>> random_state = 12883823
>>> rkf = RepeatedKFold(n_splits=2, n_repeats=2, random_state=random_state)
>>> for train, test in rkf.split(X):
... print("%s %s" % (train, test))
...
[2 3] [0 1]
[0 1] [2 3]
[0 2] [1 3]
[1 3] [0 2]
1.2.3 LeaveOneOut()
Leave One Out (LOO)留一法
相当于 Kfold 的k 取 n-1
作为一般规则,大多数作者和经验证据表明, 5- 或者 10- 交叉验证应该优于 LOO 。
1.2.4 LeavePOut()
Leave P Out (LPO) 与 Leave One Out (LOO)类似。
1.2.5 ShuffleSplit()
ShuffleSplit 迭代器 将会生成一个用户给定数量的独立的训练/测试数据划分。样例首先被打散然后划分为一对训练测试集合。
>>> from sklearn.model_selection import ShuffleSplit
>>> X = np.arange(5)
>>> ss = ShuffleSplit(n_splits=3, test_size=0.25,
... random_state=0)
>>> for train_index, test_index in ss.split(X):
... print("%s %s" % (train_index, test_index))
...
[1 3 4] [2 0]
[1 4 3] [0 2]
[4 0 2] [1 3]
可视化过程:
注意:ShuffleSplit() 不受分类和分组的影响。
 ShuffleSplit 可以替代 KFold 交叉验证,因为其提供了细致的训练 / 测试划分的 数量和样例所占的比例等的控制。
ShuffleSplit 可以替代 KFold 交叉验证,因为其提供了细致的训练 / 测试划分的 数量和样例所占的比例等的控制。
接下来的是另一类方法(变种):基于类标签、具有分层的交叉验证迭代器
一些分类问题在目标类别的分布上可能表现出很大的不平衡性:例如,可能会出现比正样本多数倍的负样本。在这种情况下,建议采用如 StratifiedKFold 和 StratifiedShuffleSplit 中实现的分层抽样方法,确保相对的类别频率在每个训练和验证 折叠 中大致保留。
1.2.6 StratifiedKFold (分层 K折)
StratifiedKFold 是 k-fold 的变种,会返回 stratified(分层) 的折叠:每个小集合中, 各个类别的样例比例大致和完整数据集中相同。
1.2.7 ShuffleSplit (分层随机)
- ShuffleSplit
- StratifiedShuffleSplit
基于这类方法的用于分组数据的交叉验证迭代器
暂略
1.3 关于shuffling的一点说明
如果数据的顺序不是任意的(比如说,相同标签的样例连续出现),为了获得有意义的交叉验证结果,首先对其进行 打散是很有必要的。然而,当样例不是独立同分布时打散则是不可行的。

1.4 交叉验证模型选择
交叉验证迭代器可以通过网格搜索得到最优的模型超参数,从而直接用于模型的选择。
详细部分看下面的章节。
2. 调整评估器的超参数
超参数,说白了就是在模型构造时人为设定的一些参数,比如 SVM 的 c、kernnel 和 gamma 和用于 Lasso 的 alpha 等。
通过专业化的、高效的参数搜索策略可以找到优化的参数,进而提升交叉验证的分数。
在 scikit-learn 包中提供了两种采样搜索候选的通用方法:GridSearchCV和RandomizedSearchCV
2.1 GridSearchCV():穷尽的网格搜索
对于给定的值, GridSearchCV 考虑了所有参数组合。
param_grid = [
{'C': [1, 10, 100, 1000], 'kernel': ['linear']},
{'C': [1, 10, 100, 1000], 'gamma': [0.001, 0.0001], 'kernel': ['rbf']},
]
2.2 RandomizedSearchCV(): 随机参数优化
RandomizedSearchCV 可以从具有指定分布的参数空间中抽取给定数量的候选。
{'C': scipy.stats.expon(scale=100), 'gamma': scipy.stats.expon(scale=.1),
'kernel': ['rbf'], 'class_weight':['balanced', None]}
2.3 参数搜索技巧
指定目标指标(metric)
为评估指定多个指标
综合评估和参数空间
模型选择:开发和评估
并行机制
对故障的鲁棒性
2.4 暴力参数搜索的替代
模型特定交叉验证
某些模型可以与参数的单个值的估计值一样有效地适应某一参数范围内的数据。 此功能可用于执行更有效的交叉验证, 用于此参数的模型选择。
该策略最常用的参数是编码正则化矩阵强度的参数。在这种情况下, 我们称之为, 计算估计器的正则化路径(regularization path)。
信息标准
出袋估计
3. 指标和评分:量化预测的质量
sklearn中有三个不同的API 用来量化模型的预测结果:
1.评估器的 score() 方法
score() 方法可以调整内置的评估标准(针对不同的任务)。
这部分在每个具体的评估器章节都有讲。
2.评分参数
cross-validation,依靠一个内部的评分策略( internal scoring strategy )对模型进行评估。
3.评分函数:metrics 模块里面包含了针对不同任务的评分函数,比如分类metrics、多标签排序metrics、回归metrics和聚类metrics。
官网这段话把我绕晕,其实一句话,模型的评估使用的是 sklearn.metrics 模块中的各类的评分函数(比如cross_val_score()),同时也可以调整评分参数内的参数来调整评估标准(比如accurency 或者f1等)。
最后, 虚拟评估器(Dummy estimators)用于获取随机预测的这些指标的基准值。
3.1 不同评分方法的scoring参数
不同的scoring参数定义了模型评估规则。
3.1.1 常见场景: 预定义值
例子:
>>> from sklearn import svm, datasets
>>> from sklearn.model_selection import cross_val_score
>>> X, y = datasets.load_iris(return_X_y=True)
>>> clf = svm.SVC(random_state=0)
>>> cross_val_score(clf, X, y, cv=5, scoring='recall_macro')
array([0.96..., 0.96..., 0.96..., 0.93..., 1. ])
>>> model = svm.SVC()
>>> cross_val_score(model, X, y, cv=5, scoring='wrong_choice')
Traceback (most recent call last):
ValueError: 'wrong_choice' is not a valid scoring value. Use sorted(sklearn.metrics.SCORERS.keys()) to get valid options.
3.1.2 定义自己的评分策略
3.1.3 定义自己的评分模块
从头开始构建自己的 scoring object 。
3.1.4 使用多个指标
Scikit-learn 还允许在 GridSearchCV, RandomizedSearchCV 和 cross_validate 中评估 multiple metric (多个指数)。
3.2 分类指标
sklearn.metrics 模块实现了几个 loss, score, 和 utility 函数来衡量 classification (分类)性能。
3.2.1 从二分到多分类和 multilabel
3.2.2 精确度得分
- accuracy_score()
3.2.3 平衡的准确度评分
- balanced accuracy()
3.2.4 Cohen’s kappa
- cohen_kappa_score()
3.2.5 混淆矩阵
- confusion_matrix()
>>> from sklearn.metrics import confusion_matrix
>>> y_true = [2, 0, 2, 2, 0, 1]
>>> y_pred = [0, 0, 2, 2, 0, 2]
>>> confusion_matrix(y_true, y_pred)
array([[2, 0, 0],
[0, 0, 1],
[1, 0, 2]])
使用参数 normalize 可以选择显示比率而不是个数:
>>> y_true = [0, 0, 0, 1, 1, 1, 1, 1]
>>> y_pred = [0, 1, 0, 1, 0, 1, 0, 1]
>>> confusion_matrix(y_true, y_pred, normalize='all')
array([[0.25 , 0.125],
[0.25 , 0.375]])
可视化混淆矩阵使用:plot_confusion_matrix()

3.2.6 分类报告
- classification_report()
>>> from sklearn.metrics import classification_report
>>> y_true = [0, 1, 2, 2, 0]
>>> y_pred = [0, 0, 2, 1, 0]
>>> target_names = ['class 0', 'class 1', 'class 2']
>>> print(classification_report(y_true, y_pred, target_names=target_names))
precision recall f1-score support
class 0 0.67 1.00 0.80 2
class 1 0.00 0.00 0.00 1
class 2 1.00 0.50 0.67 2
accuracy 0.60 5
macro avg 0.56 0.50 0.49 5
weighted avg 0.67 0.60 0.59 5
3.2.7 Hamming loss (汉明损失)
hamming_loss 计算两组样本之间的 average Hamming loss (平均汉明损失)或者 Hamming distance(汉明距离) 。
3.2.8 Precision, recall and F-measures(精确率、召回率、F 值-度量)
3.2.8.1 二分类
3.2.8.2 多分类和多标签分类
3.2.9Jaccard 相似性系数分数
3.2.10 Hinge 损失
hinge_loss() 使用 hinge loss 计算模型和数据之间的 average distance (平均距离),这是一种只考虑 prediction errors (预测误差)的 one-sided metric (单向指标)。(Hinge loss 用于最大边界分类器,如支持向量机)
3.2.11 Log 损失
Log loss,又被称为 logistic regression loss(logistic 回归损失)或者 cross-entropy loss(交叉熵损失) 定义在 probability estimates (概率估计)。它通常用于 (multinomial) logistic regression ((多项式)logistic 回归)和 neural networks (神经网络)以及 expectation-maximization (期望最大化)的一些变体中,并且可用于评估分类器的 probability outputs (概率输出)(predict_proba)而不是其 discrete predictions (离散预测)。
3.2.12 Matthews 相关系数
3.2.13 多标签混合矩阵
3.2.14 受试者工作特性曲线 (ROC)
3.2.15 零一损失
- zero_one_loss()
3.2.16 Brier 分数损失
- brier_score_loss()
3.3 多标签排序指标
3.4 回归指标
3.4.1 解释方差得分
3.4.2 最大误差
- max_error()
3.4.3 平均绝对值
3.4.4 均方误差
3.4.5 均方误差对数
3.4.6 中位绝对误差
- median_absolute_error()
R² score, 可决系数
聚类指标
暂略
虚拟估计: DummyClassifier()
在进行监督学习的过程中,简单的 sanity check(理性检查)将我们训练的评估器与简单的经验法则进行比较。
4. 模型持久化
在训练完 scikit-learn 模型之后,最好有一种方法来将模型持久化以备将来使用,而无需重新训练。
可以通过使用 Python 的内置持久化模型将训练好的模型保存在 scikit 中它名为 pickle:
>>> from sklearn import svm
>>> from sklearn import datasets
>>> clf = svm.SVC()
>>> iris = datasets.load_iris()
>>> X, y = iris.data, iris.target
>>> clf.fit(X, y)
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='auto', kernel='rbf',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)
>>> import pickle
>>> s = pickle.dumps(clf)
>>> clf2 = pickle.loads(s)
>>> clf2.predict(X[0:1])
array([0])
>>> y[0]
0
5. 验证曲线:绘制分数图来评估模型
每种评估器都有其优势和缺陷。它的泛化误差可以用偏差、方差和噪声来分解。
估计值的偏差 是不同训练集的平均误差。估计值的方差用来表示它对训练集的变化有多敏感。噪声是数据的一个属性。
5.1 验证曲线(validation curve)
绘制单个超参数对训练分数和验证分数的影响,有时有助于发现该估计是否因为某些超参数的值 而出现过拟合或欠拟合。
>>> from sklearn.model_selection import validation_curve
>>> from sklearn.datasets import load_iris
>>> from sklearn.linear_model import Ridge
>>> np.random.seed(0)
>>> X, y = load_iris(return_X_y=True)
>>> indices = np.arange(y.shape[0])
>>> np.random.shuffle(indices)
>>> X, y = X[indices], y[indices]
>>> train_scores, valid_scores = validation_curve(Ridge(), X, y, "alpha",
... np.logspace(-7, 3, 3),
... cv=5)
>>> train_scores
array([[0.93..., 0.94..., 0.92..., 0.91..., 0.92...],
[0.93..., 0.94..., 0.92..., 0.91..., 0.92...],
[0.51..., 0.52..., 0.49..., 0.47..., 0.49...]])
>>> valid_scores
array([[0.90..., 0.84..., 0.94..., 0.96..., 0.93...],
[0.90..., 0.84..., 0.94..., 0.96..., 0.93...],
[0.46..., 0.25..., 0.50..., 0.49..., 0.52...]])
在这里插入代码片
如果训练得分和验证得分都很低,则估计器是不合适的。如果训练得分高,验证得分低,则估计器过拟合, 否则估计会拟合得很好。通常不可能有较低的训练得分和较高的验证得分。所有三种情况都可以 在下面的图中找到,其中我们改变了数字数据集上 SVM 的参数 gamma 。

5.2 学习曲线
学习曲线显示了对于不同数量的训练样本的估计器的验证和训练评分。它可以帮助我们发现从增加更多的训 练数据中能获益多少,以及估计是否受到更多来自方差误差或偏差误差的影响。如果在增加训练集大小时,验证分数和训练 分数都收敛到一个很低的值,那么我们将不会从更多的训练数据中获益。在下面的图中看到一个例子:朴素贝叶斯大致收敛到一个较低的分数。
 )
)
>>> from sklearn.model_selection import learning_curve
>>> from sklearn.svm import SVC
>>> train_sizes, train_scores, valid_scores = learning_curve(
... SVC(kernel='linear'), X, y, train_sizes=[50, 80, 110], cv=5)
>>> train_sizes
array([ 50, 80, 110])
>>> train_scores
array([[0.98..., 0.98 , 0.98..., 0.98..., 0.98...],
[0.98..., 1. , 0.98..., 0.98..., 0.98...],
[0.98..., 1. , 0.98..., 0.98..., 0.99...]])
>>> valid_scores
array([[1. , 0.93..., 1. , 1. , 0.96...],
[1. , 0.96..., 1. , 1. , 0.96...],
[1. , 0.96..., 1. , 1. , 0.96...]])
写在后面
sklearn 里面的内容真的很全面,这部分看第一遍的途中有几次由于关注细节而陷了进去,差点忘了大方向。话不多说,在此做个梳理,对这部分做个总结:
- what
- how