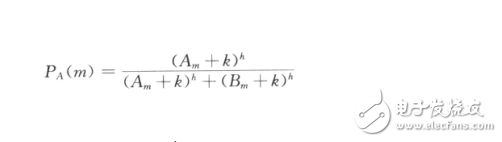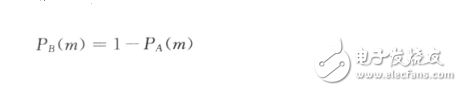蚁群算法matlab案例,蚁群算法即相关代码实现详解—matlab之智能算法
描述
蚁群算法即相关代码实现详解
一.算法背景
蚁群算法是近年来刚刚诞生的随机优化方法,它是一种源于大自然的新的仿生类算法.由意大利学者Dorigo最早提出,蚂蚁算法主要是通过蚂蚁群体之间的信息传递而达到寻优的目的,最初又称蚁群优化方法(Ant Colony Optimization简称ACO).由于模拟仿真中使用了人工蚂蚁的概念,因此亦称蚂蚁系统.
二.简单说明
1)先看两张图
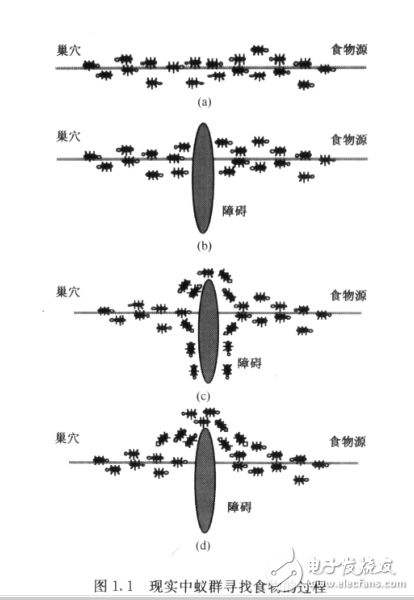
图1-1显示了蚂蚁从巢穴出去觅食的过程,起初在遇到障碍的时候,会以相同的概率选择通过障碍的路径(即选择了两条路径假设为路径1和2,且每条路径上的蚂蚁数量是相同的).而在图1-1(d)中,蚂蚁们却不再选择路径(2)),这就是蚁群算法的“双桥模型”,这是什么原因呢?
2)算法探究
经过探究,上述的实验反应了蚂蚁在群体行为中的一种信息正反馈现象.蚂蚁个体间通过这种信息交流机制来搜索食物.而用来交流反馈的化学因素现在被我们称之为——————“信息素”.
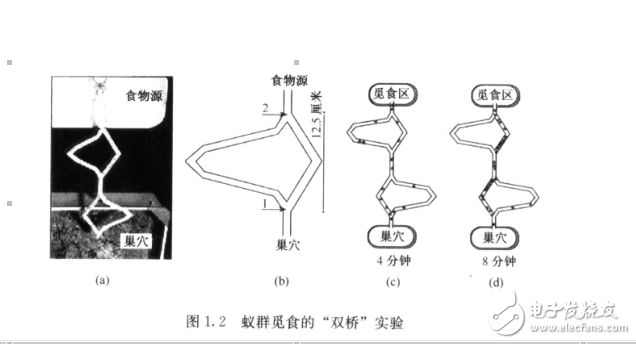
然后建立相关“双桥”实验的数学模型,首先,假设在对称桥的信息素的总数与过去一段时间内经过该桥的蚂蚁数目成正比(即每只蚂蚁都具有相同的信息素释放能力);其次,假设某时刻蚂蚁按照桥上残留信息量的多少来选择其中的某条路径,经过该路径的蚂蚁数目越多,则该桥上的残留信息素总量就越大.假设1-1图中的两条路径分别为A和B,Am和Bm分别表示通过路径A和B的蚂蚁数目.则当所有M(Am+Bm=M)只蚂蚁通过障碍后,第(M+1)只蚂蚁选择路径A的概率为
相反选择路径B的概率为
其中参数h(期望因子)和k(启发因子)用来匹配真实实验数据,第(M+1)只蚂蚁按照上述公式计算概率,然后生成一个区间在[0,1]上均匀分布的随机数w,若w<=P(A),则选择路径A,否则选择路径B.
三.matlab相关代码实现(以TSP旅行商问题为例)
以下是解放军信息工程大学一个老师编的matlab程序,网上有很多版本,已经由本人添加注释并修改过请尊重原作者劳动,引用时请注明出处.
%符号说明
%SumOfant表示蚂蚁数量
%SumOfCity表示城市数量
%sight为距离的倒数,表示每条边的能见度
%Q表示信息素增强的系数
%nc_now表示当前的迭代次数
%nc_max表示自主设置的最大迭代次数 表示终止条件
%first_address表示测试数据中的城市坐标
%RouteOfBest表示各代的最佳路线
%LengthOfBest表示每次迭代的最佳路线的长度
%a表示启发因子,表示信息素的相对重要程度
%b表示期望因子,表示能见度的重要性
%p表示信息素的蒸发系数,(1-p)表示信息素持久性系数
%length_address表示两两城市间的距离
for n=1:size(first_address)
for m=1:size(first_address)
length_address(n,m)=[(first_address(n,1)-first_address(m,1))^2+(first_address(n,2)-first_address(m,2))^2]^1/2;
end
end
sight=1./length_address;%表示每条边的能见度
SumOfCity=20;
>> SumOfant=40;
>> sight=1./length_address;
info_pre=ones(SumOfCity,SumOfCity);
%info_pre为信息素矩阵,可以理解为在蚂蚁还没有被放入城市前,每条道路上就已经存在了一定含量的信息素(只是为了方便计算)
>> EachOfRoute=zeros(SumOfCity,SumOfCity);
> %存储并记录每次迭代时每只蚂蚁经历的路径生成;
>> nc_now=1; nc_max=60; %迭代计数器,记录迭代次数,此处设置为60次迭代
>> RouteOfBest=zeros(nc_max,SumOfCity); %各代最佳路线
Length_best=inf.*ones(nc_max,1); %各代最佳路线的长度
LengthOfAverage=zeros(nc_max,1); %各代路线的平均长度
while nc_now<=nc_max%表示循环终止条件,迭代终止器
%%第二步:将m只蚂蚁放到n个城市上
Randpos=[]; %随即存取
for i=1:(ceil(SumOfant/SumOfCity))
%ceil为取整函数,表示每个城市放几只蚂蚁
Randpos=[Randpos,randperm(SumOfCity)];
%randperm表示1-20随机分配,也就是每只蚂蚁的位置
end %表示每只蚂蚁一开始所被放置的位置%第三步:所有蚂蚁按概率函数选择下一座城市,完成各自的周游
for j=2:SumOfCity %每只蚂蚁从第一个城市出发,开始依次访问
for i=1:SumOfant CityOfVisited=EachOfRoute(i,1:(j-1)); %记录已访问的城市,避免重复访问
J=zeros(1,(SumOfCity-j+1)); %待访问的城市
P=J;
%待访问城市的选择概率分布,用P表示
Jc=1;%记录已经访问的城市数目
for k=1:SumOfCity
if length(find(CityOfVisited==k))==0 %开始时置0
J(Jc)=k; Jc=Jc+1; %访问的城市个数自加1
end
end
%下面计算待选城市的概率分布
for k=1:length(J)%对每只蚂蚁还没有访问的城市依次计算概率
P(k)=(info_pre(CityOfVisited(end),J(k))^0.7)*(sight(CityOfVisited(end),J(k))^3.8);%在这里设置启发因子=0.7,期望因子=3.8 end P=P/(sum(P));%按概率原则选取下一个城市
Pcum=cumsum(P); %cumsum,元素累加即求和
Select=find(Pcum>=rand); %若计算的概率大于原来的就选择这条路线
CityOfNextVisit=J(Select(1));
EachOfRoute(i,j)=CityOfNextVisit;
end
end
if nc_now>=2
EachOfRoute(1,:)=RouteOfBest(nc_now-1,:);
%如果迭代次数大于2,则将前依次迭代的访问顺序存入EachOfRoute
end%%第四步:记录本次迭代最佳路线
L=zeros(SumOfant,1); %开始距离为0,m*1的列向量
for i=1:SumOfant
R=EachOfRoute(i,:);
其中DrawRoute为自己写的一个画图函数,推荐程序如下
打开APP阅读更多精彩内容
点击阅读全文