1.4+1.5 L1、L2正则化

2022.08.27 李航老师《统计学习方法》： 一. 统计学习及监督学习概论
# 本文目的就是为学者简化学习内容，提取我认为的重点 把书读薄;
# 本文重点：1.5 正则化理解

一. 统计学习及监督学习概论

1.4+1.5 L1、L2正则化

1.4 模型评估与模型选择

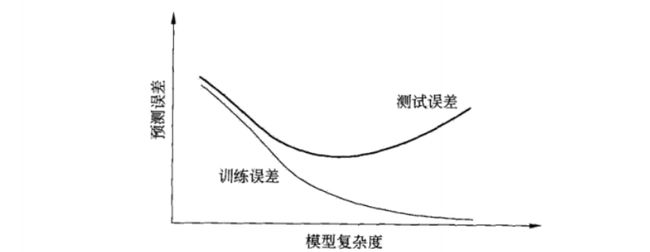
1.4.1 训练误差与测试误差

• 目的不仅仅是对已知数据，更重要的是未知数据有更好的预测能力。测试误差越小，预测能力越强。
• 不同的学习方法，测试误差可能不同，所以较小的是更好的。

m=0： 就是未知数最高是0次幂 y=C 是条平行于x轴的线；
m=1：就是未知数最高是1次幂 y=kx+b 是条斜线；

• 我们发现：次数越高，穿过的训练数据越多，图形越复杂。也就是：函数越复杂，对训练集拟合就约好。

越复杂的函数，训练数据误差是逐步减小的，但在预测未知数据时是误差是先减小后增大的，原因就是过拟合。

1.5 正则化与交叉检验

1.5.1.1 正则化

机器学习会出现过拟合的现象，如何解决？ 正则化。

$$\underset{f\in F}{\min }\frac{1}{N}\sum _{i=1}^{N}L(y_i,f(x_i))+\lambda J(f)$$

其中，$\lambda J(f)$为正则化项。

1. 什么是正则化？
   减少泛化误差的方法，也就是减少过拟合的方法，也就是不是减少训练误差而是减少测试误差的方法。

2. 我们怎么思考去正则化限制测试误差？ 有两个角度

   第一种理解：见【图 1.8】，上一章有讲，未知数次数越高，泛化能力就约差，越容易过拟合，我们应该适当的限制次数；限制方法就是在适当的位置m开始小到$w_m,w_{m+1},...$均为0 ；
   第二种理解：我们在训练神经网络的时候，比如输出层的输入：
   $$z^{[l]}=W^{[l{]}^T}\cdot a^{[l-1]}+b^{[l]}$$

   • l是输出层，之前是隐藏层。就是用第l-1层输出的结果a带入到第l层神经网络上计算。
   • 我们把隐藏层的w和b均扩大2倍时,那么l层输入变为了$2^{(l-1)}{a}^{[l-1]}$, 我们把输出层W缩小$2^{(l-1)}$倍，那么$z^{[l]}$不变。
     $$z^{[l]}=\frac{1}{2^{(l-1)}}\cdot W^{[l{]}^T}\cdot 2^{(l-1)}\cdot a^{[l-1]}+b^{[l]}$$

   也就是我们收敛到同样的情况，可能存在多组w,b。而在较大的w下，误差也会被放大。

综上所述，我们主要是控制w来去过拟合的，让w尽可能的小

3. 如何去控制w?

正则化项可以取不同形式,常用L1,L2，dropout等正则化，本章主要讲L1,L2正则化:

• L1正则化：指权值向量 w 中各个元素的绝对值之和.

$$L(w)=\frac{1}{N}\sum _{i=1}^{N}L(y_i,f(x_i))+\lambda {\left|\left|w\right|\right|}_1$$$$l_1:{\left|\left|w\right|\right|}_1=\sum _i\left|w_i\right|$$

• L2正则化: 指权值向量 w 中各个元素的平方和再开平方。
  $$L(w)=\frac{1}{N}\sum _{i=1}^{N}L(y_i,f(x_i))+\frac{\lambda }{2}{\left|\left|w\right|\right|}^2$$$$l_2:{\left|\left|w\right|\right|}^2={\left|\left|w\right|\right|}_2^2=\sum _i{w}_i^2$$

4. 怎么理解这个正则化能控制w?

• 就是规范w的范围，b是平移效果，所以不用考虑，w约束好了，b训练的时候跟着就被约束好了。

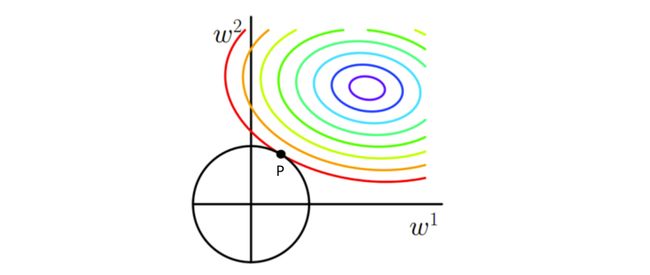
• 我们以L2举例，w选了两个维度，我们约束L2在C范围内：

$$求：minJ(W)；$$$$条件：任意取值s.t.{\left|\left|w\right|\right|}^2-C⩽0$$

• 把俩条件合起来;

$$L(W,\lambda )=J(W)+\lambda ({\left|\left|w\right|\right|}^2-C)$$$$求：\underset{w}{\min }\underset{\lambda }{\max }L(W,\lambda )$$

p点就是极小值点。

因为只有在相切点时候，梯度才可能大小相等，方向相反。也就是$\nabla L(W_p,{\lambda }_p)=0$,取得极小值点（$w_p^1,w_p^2$）.

1.5.1.2 拉个朗日角度理解L2正则化

拉格朗日乘数法：

1. 拉格朗日乘数法

$$L(W,\lambda )=J(W)+\lambda ({\left|\left|w\right|\right|}^2-C)$$$$求：\underset{w}{\min }\underset{\lambda }{\max }L(W,\lambda )$$

2. L2与拉格朗日乘数法%L_拉%对比

$$L_{拉}(W,\lambda )=J(W)+\lambda {\left|\left|w\right|\right|}^2-\lambda C$$$$L_2(W,\lambda )=J(W)+\lambda {\left|\left|w\right|\right|}^2$$

• $L_{拉}$中，半径C是超参数，而$\lambda$是可以通过C、J(w)梯度求出来的（大小相等，方向相反）；

• $L_2$中，$\lambda$控制梯度步伐，是超参数。$\lambda$确定，那么梯度位置就确定了。

• 拉格朗日乘数法求的极值和L2正则化求的极值时，极值点w是一致的（极小值可能有所不同）
  $$\underset{w}{\arg }（\underset{w}{\min }\underset{\lambda }{\max }{L}_{拉}(W,\lambda )）=\underset{w}{\arg }（\underset{w}{\min }\underset{\lambda }{\max }{L}_2(W,\lambda )）$$$$s.t.\lambda ⩾0$$

1.5.1.3 L1\L2正则化图像和相应特性

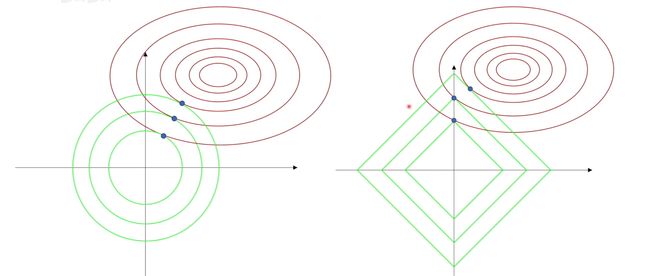
• L1 正则化优点：可以带来稀疏性，也就是如图，有些切点有可能落在坐标轴上。也就是，L1正则化后，很有可能出现有些w有值，有些w没值；也就是有些体征起作用，有些特征不起作用。

  比如判断是猫是狗…以前要看耳朵 眉毛啥的 经过L1正则化,有可能 只看耳朵这个特征，就能区分是猫是狗了

• L2 正则化优点：计算方便（因为存在解析解）

• 可以直接求导获得取最小值时各个参数的取值。

1.5.2 交叉验证

1. 简单交叉验证

   就是给的数据随机出来两部分，一部分做训练集，一部分做测试集；然后不同参数训练训练集，用测试集来看模型误差；误差最小的就是所求的。

2. s折交叉验证

   就是将已给数据分成s个互不相交、大小相等的子集，选s-1个子集做训练集，另一个做测试集；这样重复s遍，选出误差最小的模型。