机器学习7-逻辑斯蒂回归实现西瓜数据集2.0的二分类
文章目录
- 1 什么是逻辑回归
- 1.1 Sigmoid函数介绍
- 2 逻辑回归公式推导
-
- 2.1 损失函数推导
- 3 逻辑回归迭代公式
-
- 3.1 函数特性
- 3.2 求导过程
- 4 逻辑回归实现西瓜数据集2.0的分类
我们在实现西瓜数据集2.0分类之前先讲讲逻辑回归的原理。
1 什么是逻辑回归
逻辑回归不是一个回归的算法,逻辑回归是一个分类的算法,好比卡巴斯基不是司机,红烧狮子头没有狮子头一样。 那为什么逻辑回归不叫逻辑分类?因为逻辑回归算法是基于多元线性回归的算法。而正因为此,逻辑回归这个分类算法是线性的分类器。
逻辑回归算法(LogisticRegression)是分类算法,我们将它作为分类算法使用。有时候可能因为这个算法的名字中出现了“回归”使你感到困惑,但逻辑回归算法实际上是一种分类算法,它适用于标签 y 取值离散的情况,如:1 0 0 1。
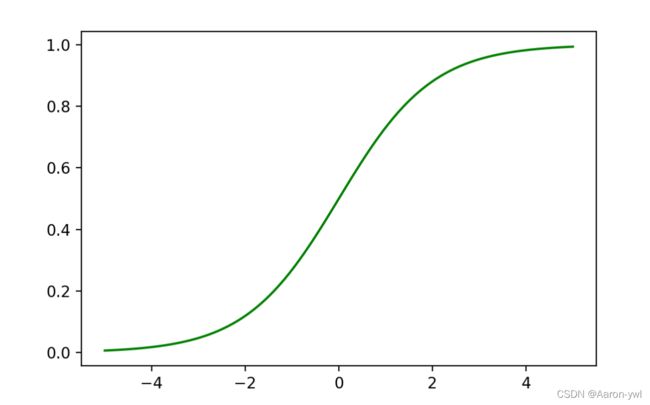
逻辑回归中对应一条非常重要的曲线S型曲线,对应的函数是Sigmoid函数:
f ( x ) = 1 1 + e − x f(x) = \frac{1}{1 + e^{-x}} f(x)=1+e−x1
它有一个非常棒的特性,其导数可以用其自身表示:
f ′ ( x ) = e − x ( 1 + e − x ) 2 = f ( x ) ∗ 1 + e − x − 1 1 + e − x = f ( x ) ∗ ( 1 − f ( x ) ) f'(x) = \frac{e^{-x}}{(1 + e^{-x})^2} =f(x) * \frac{1 + e^{-x} - 1}{1 + e^{-x}} = f(x) * (1 - f(x)) f′(x)=(1+e−x)2e−x=f(x)∗1+e−x1+e−x−1=f(x)∗(1−f(x))
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1/(1 + np.exp(-x))
x = np.linspace(-5,5,100)
y = sigmoid(x)
plt.plot(x,y,color = 'green')
1.1 Sigmoid函数介绍
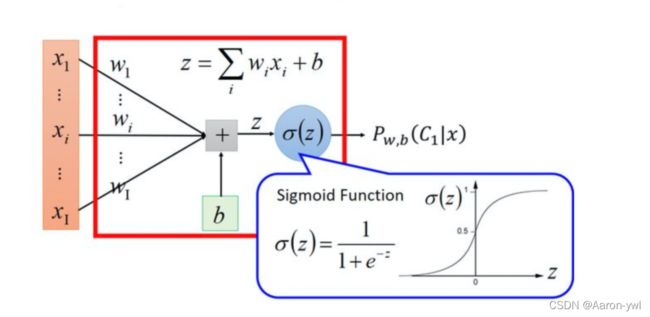
逻辑回归就是在多元线性回归基础上把结果缩放到 0 ~ 1 之间。 h θ ( x ) h_{\theta}(x) hθ(x) 越接近 1 越是正例, h θ ( x ) h_{\theta}(x) hθ(x) 越接近 0 越是负例,根据中间 0.5 将数据分为二类。其中 h θ ( x ) h_{\theta}(x) hθ(x) 就是概率函数~
h θ ( x ) = g ( θ T x ) = 1 1 + e − θ T x h_{\theta}(x) = g(\theta^Tx) = \frac{1}{1 + e^{-\theta^Tx}} hθ(x)=g(θTx)=1+e−θTx1
我们知道分类器的本质就是要找到分界,所以当我们把 0.5 作为分类边界时,我们要找的就是 y ^ = h θ ( x ) = 1 1 + e − θ T x = 0.5 \hat{y} = h_{\theta}(x) = \frac{1}{1 + e^{-\theta^Tx}} = 0.5 y^=hθ(x)=1+e−θTx1=0.5 ,即 z = θ T x = 0 z = \theta^Tx = 0 z=θTx=0 时, θ \theta θ 的解~
求解过程如下:
什么事情,都要做到知其然,知其所以然,我们知道二分类有个特点就是正例的概率 + 负例的概率 = 1。一个非常简单的试验是只有两种可能结果的试验,比如正面或反面,成功或失败,有缺陷或没有缺陷,病人康复或未康复等等。为方便起见,记这两个可能的结果为 0 和 1,下面的定义就是建立在这类试验基础之上的。 如果随机变量 x 只取 0 和 1 两个值,并且相应的概率为:
- P r ( x = 1 ) = p ; P r ( x = 0 ) = 1 − p ; 0 < p < 1 Pr(x = 1) = p; Pr(x = 0) = 1-p; 0 < p < 1 Pr(x=1)=p;Pr(x=0)=1−p;0<p<1
则称随机变量 x 服从参数为 p 的Bernoulli伯努利分布( 0-1分布),则 x 的概率函数可写:
- f ( x ∣ p ) = { p x ( 1 − p ) 1 − x , x = 1 、 0 0 , x ≠ 1 、 0 f(x | p) = \begin{cases}p^x(1 - p)^{1-x}, &x = 1、0\\0,& x \neq 1、0\end{cases} f(x∣p)={px(1−p)1−x,0,x=1、0x=1、0
逻辑回归二分类任务会把正例的 label 设置为 1,负例的 label 设置为 0,对于上面公式就是 x = 0、1。
2 逻辑回归公式推导
2.1 损失函数推导
这里我们依然会用到最大似然估计思想,根据若干已知的 X,y(训练集) 找到一组 θ \theta θ 使得 X 作为已知条件下 y 发生的概率最大。
关于什么是最大似然估计可以参考我这篇文章哦:机器学习4-线性回归算法推导
P ( y ∣ x ; θ ) = { h θ ( x ) , y = 1 1 − h θ ( x ) , y = 0 P(y|x;\theta) = \begin{cases}h_{\theta}(x), &y = 1\\1-h_{\theta}(x),& y = 0\end{cases} P(y∣x;θ)={hθ(x),1−hθ(x),y=1y=0
整合到一起(二分类就两种情况:1、0)得到逻辑回归表达式:
P ( y ∣ x ; θ ) = ( h θ ( x ) ) y ( 1 − h θ ( x ) ) 1 − y P(y|x;\theta) = (h_{\theta}(x))^{y}(1 - h_{\theta}(x))^{1-y} P(y∣x;θ)=(hθ(x))y(1−hθ(x))1−y
我们假设训练样本相互独立,那么似然函数表达式为:
L ( θ ) = ∏ i = 1 n P ( y ( i ) ∣ x ( i ) ; θ ) L(\theta) = \prod\limits_{i = 1}^nP(y^{(i)}|x^{(i)};\theta) L(θ)=i=1∏nP(y(i)∣x(i);θ)
L ( θ ) = ∏ i = 1 n ( h θ ( x ( i ) ) ) y ( i ) ( 1 − h θ ( x ( i ) ) ) 1 − y ( i ) L(\theta) = \prod\limits_{i=1}^n(h_{\theta}(x^{(i)}))^{y^{(i)}}(1 - h_{\theta}(x^{(i)}))^{1-y^{(i)}} L(θ)=i=1∏n(hθ(x(i)))y(i)(1−hθ(x(i)))1−y(i)
对数转换,自然底数为底
l ( θ ) = ln L ( θ ) = ln ( ∏ i = 1 n ( h θ ( x ( i ) ) ) y ( i ) ( 1 − h θ ( x ( i ) ) ) 1 − y ( i ) ) l(\theta) = \ln{L(\theta)} =\ln( \prod\limits_{i=1}^n(h_{\theta}(x^{(i)}))^{y^{(i)}}(1 - h_{\theta}(x^{(i)}))^{1-y^{(i)}}) l(θ)=lnL(θ)=ln(i=1∏n(hθ(x(i)))y(i)(1−hθ(x(i)))1−y(i))
化简,累乘变累加:
l ( θ ) = ln L ( θ ) = ∑ i = 1 n ( y ( i ) ln ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) ln ( 1 − h θ ( x ( i ) ) ) ) l(\theta) = \ln{L(\theta)} = \sum\limits_{i = 1}^n(y^{(i)}\ln(h_{\theta}(x^{(i)})) + (1-y^{(i)})\ln(1-h_{\theta}(x^{(i)}))) l(θ)=lnL(θ)=i=1∑n(y(i)ln(hθ(x(i)))+(1−y(i))ln(1−hθ(x(i))))
总结,得到了逻辑回归的表达式,下一步跟线性回归类似,构建似然函数,然后最大似然估计,最终推导出 θ \theta θ 的迭代更新表达式。只不过这里用的不是梯度下降,而是梯度上升,因为这里是最大化似然函数。通常我们一提到损失函数,往往是求最小,这样我们就可以用梯度下降来求解。最终损失函数就是上面公式加负号的形式:
J ( θ ) = − l ( θ ) = − ∑ i = 1 n [ y ( i ) ln ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) ln ( 1 − h θ ( x ( i ) ) ) ] J(\theta) = -l(\theta) = -\sum\limits_{i = 1}^n[y^{(i)}\ln(h_{\theta}(x^{(i)})) + (1-y^{(i)})\ln(1-h_{\theta}(x^{(i)}))] J(θ)=−l(θ)=−i=1∑n[y(i)ln(hθ(x(i)))+(1−y(i))ln(1−hθ(x(i)))]
3 逻辑回归迭代公式
3.1 函数特性
逻辑回归参数更新规则:
θ j t + 1 = θ j t − α ∂ ∂ θ j J ( θ ) \theta_j^{t + 1} = \theta_j^t - \alpha\frac{\partial}{\partial_{\theta_j}}J(\theta) θjt+1=θjt−α∂θj∂J(θ)
- α \alpha α 表示学习率
逻辑回归函数:
h θ ( x ) = g ( θ T x ) = g ( z ) = 1 1 + e − z h_{\theta}(x) = g(\theta^Tx) = g(z) = \frac{1}{1 + e^{-z}} hθ(x)=g(θTx)=g(z)=1+e−z1
- z = θ T x z = \theta^Tx z=θTx
逻辑回归函数求导时有一个特性,这个特性将在下面的推导中用到,这个特性为:
g ′ ( z ) = ∂ ∂ z 1 1 + e − z = e − z ( 1 + e − z ) 2 = 1 ( 1 + e − z ) 2 ⋅ e − z = 1 1 + e − z ⋅ ( 1 − 1 1 + e − z ) = g ( z ) ⋅ ( 1 − g ( z ) ) \begin{aligned} g'(z) &= \frac{\partial}{\partial z}\frac{1}{1 + e^{-z}} \\\\&= \frac{e^{-z}}{(1 + e^{-z})^2}\\\\& = \frac{1}{(1 + e^{-z})^2}\cdot e^{-z}\\\\&=\frac{1}{1 + e^{-z}} \cdot (1 - \frac{1}{1 + e^{-z}})\\\\&=g(z)\cdot (1 - g(z))\end{aligned} g′(z)=∂z∂1+e−z1=(1+e−z)2e−z=(1+e−z)21⋅e−z=1+e−z1⋅(1−1+e−z1)=g(z)⋅(1−g(z))
回到逻辑回归损失函数求导:
J ( θ ) = − ∑ i = 1 n ( y ( i ) ln ( h θ ( x i ) ) + ( 1 − y ( i ) ) ln ( 1 − h θ ( x ( i ) ) ) ) J(\theta) = -\sum\limits_{i = 1}^n(y^{(i)}\ln(h_{\theta}(x^{i})) + (1-y^{(i)})\ln(1-h_{\theta}(x^{(i)}))) J(θ)=−i=1∑n(y(i)ln(hθ(xi))+(1−y(i))ln(1−hθ(x(i))))
3.2 求导过程
∂ ∂ θ j J ( θ ) = − ∑ i = 1 n ( y ( i ) 1 h θ ( x ( i ) ) ∂ ∂ θ j h θ ( x i ) + ( 1 − y ( i ) ) 1 1 − h θ ( x ( i ) ) ∂ ∂ θ j ( 1 − h θ ( x ( i ) ) ) ) = − ∑ i = 1 n ( y ( i ) 1 h θ ( x ( i ) ) ∂ ∂ θ j h θ ( x ( i ) ) − ( 1 − y ( i ) ) 1 1 − h θ ( x ( i ) ) ∂ ∂ θ j h θ ( x ( i ) ) ) = − ∑ i = 1 n ( y ( i ) 1 h θ ( x ( i ) ) − ( 1 − y ( i ) ) 1 1 − h θ ( x ( i ) ) ) ∂ ∂ θ j h θ ( x ( i ) ) = − ∑ i = 1 n ( y ( i ) 1 h θ ( x ( i ) ) − ( 1 − y ( i ) ) 1 1 − h θ ( x ( i ) ) ) h θ ( x ( i ) ) ( 1 − h θ ( x ( i ) ) ) ∂ ∂ θ j θ T x = − ∑ i = 1 n ( y ( i ) ( 1 − h θ ( x ( i ) ) ) − ( 1 − y ( i ) ) h θ ( x ( i ) ) ) ∂ ∂ θ j θ T x = − ∑ i = 1 n ( y ( i ) − h θ ( x ( i ) ) ) ∂ ∂ θ j θ T x = ∑ i = 1 n ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \begin{aligned} \frac{\partial}{\partial{\theta_j}}J(\theta) &= -\sum\limits_{i = 1}^n(y^{(i)}\frac{1}{h_{\theta}(x^{(i)})}\frac{\partial}{\partial_{\theta_j}}h_{\theta}(x^{i}) + (1-y^{(i)})\frac{1}{1-h_{\theta}(x^{(i)})}\frac{\partial}{\partial_{\theta_j}}(1-h_{\theta}(x^{(i)}))) \\\\&=-\sum\limits_{i = 1}^n(y^{(i)}\frac{1}{h_{\theta}(x^{(i)})}\frac{\partial}{\partial_{\theta_j}}h_{\theta}(x^{(i)}) - (1-y^{(i)})\frac{1}{1-h_{\theta}(x^{(i)})}\frac{\partial}{\partial_{\theta_j}}h_{\theta}(x^{(i)}))\\\\&=-\sum\limits_{i = 1}^n(y^{(i)}\frac{1}{h_{\theta}(x^{(i)})} - (1-y^{(i)})\frac{1}{1-h_{\theta}(x^{(i)})})\frac{\partial}{\partial_{\theta_j}}h_{\theta}(x^{(i)})\\\\&=-\sum\limits_{i = 1}^n(y^{(i)}\frac{1}{h_{\theta}(x^{(i)})} - (1-y^{(i)})\frac{1}{1-h_{\theta}(x^{(i)})})h_{\theta}(x^{(i)})(1-h_{\theta}(x^{(i)}))\frac{\partial}{\partial_{\theta_j}}\theta^Tx\\\\&=-\sum\limits_{i = 1}^n(y^{(i)}(1-h_{\theta}(x^{(i)})) - (1-y^{(i)})h_{\theta}(x^{(i)}))\frac{\partial}{\partial_{\theta_j}}\theta^Tx\\\\&=-\sum\limits_{i = 1}^n(y^{(i)} - h_{\theta}(x^{(i)}))\frac{\partial}{\partial_{\theta_j}}\theta^Tx\\\\&=\sum\limits_{i = 1}^n(h_{\theta}(x^{(i)}) -y^{(i)})x_j^{(i)}\end{aligned} ∂θj∂J(θ)=−i=1∑n(y(i)hθ(x(i))1∂θj∂hθ(xi)+(1−y(i))1−hθ(x(i))1∂θj∂(1−hθ(x(i))))=−i=1∑n(y(i)hθ(x(i))1∂θj∂hθ(x(i))−(1−y(i))1−hθ(x(i))1∂θj∂hθ(x(i)))=−i=1∑n(y(i)hθ(x(i))1−(1−y(i))1−hθ(x(i))1)∂θj∂hθ(x(i))=−i=1∑n(y(i)hθ(x(i))1−(1−y(i))1−hθ(x(i))1)hθ(x(i))(1−hθ(x(i)))∂θj∂θTx=−i=1∑n(y(i)(1−hθ(x(i)))−(1−y(i))hθ(x(i)))∂θj∂θTx=−i=1∑n(y(i)−hθ(x(i)))∂θj∂θTx=i=1∑n(hθ(x(i))−y(i))xj(i)
求导最终的公式:
∂ ∂ θ j J ( θ ) = ∑ i = 1 n ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \frac{\partial}{\partial{\theta_j}}J(\theta) = \sum\limits_{i = 1}^n(h_{\theta}(x^{(i)}) -y^{(i)})x_j^{(i)} ∂θj∂J(θ)=i=1∑n(hθ(x(i))−y(i))xj(i)
逻辑回归参数迭代更新公式:
θ j t + 1 = θ j t − α ⋅ ∑ i = 1 n ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j^{t+1} = \theta_j^t - \alpha \cdot \sum\limits_{i=1}^{n}(h_{\theta}(x^{(i)}) -y^{(i)})x_j^{(i)} θjt+1=θjt−α⋅i=1∑n(hθ(x(i))−y(i))xj(i)
4 逻辑回归实现西瓜数据集2.0的分类
'''
属性[x]
色泽:乌黑0, 青绿1, 浅白2
根蒂:蜷缩0, 稍蜷1, 硬挺2
敲声:浊响0, 沉闷1, 清脆2
纹理:清晰0, 稍糊1, 模糊2
脐部:凹陷0, 稍凹1, 平坦2
触感:硬滑0, 软粘1
预测结果[y]
好瓜1,坏瓜0
'''
import numpy as np
from sklearn.linear_model import LogisticRegression
# 训练数据,西瓜数据集2.0,表4.2
X_train = np.array([[1, 0, 0, 0, 0, 0], [0, 0, 1, 0, 0, 0], [0, 0, 0, 0, 0, 0],
[1, 1, 0, 0, 1, 1], [0, 1, 0, 1, 1, 1], [1, 2, 2, 0, 2, 1],
[2, 1, 1, 1, 0, 0], [0, 1, 0, 0, 1, 1],[2, 0, 0, 2, 2, 0],
[1, 0, 1, 1, 1, 0]])
y_train = np.array([1, 1, 1, 1, 1, 0, 0, 0, 0, 0])
# 测试数据 表4.2
X_test = np.array([[1, 0, 1, 0, 0, 0],[2, 0, 0, 0, 0, 0],[0, 1, 0, 0, 1, 0],
[0, 1, 1, 1, 1, 0],[2, 2, 2, 2, 2, 0],[2, 0, 0, 2, 2, 1],
[1, 1, 0, 1, 0, 0]])
y_test = np.array([1, 1, 1, 0, 0, 0, 0])
# 训练
model = LogisticRegression()
model.fit(X_train,y_train)
# 预测
y_pred = model.predict(X_test)
# 显示是否预测正确
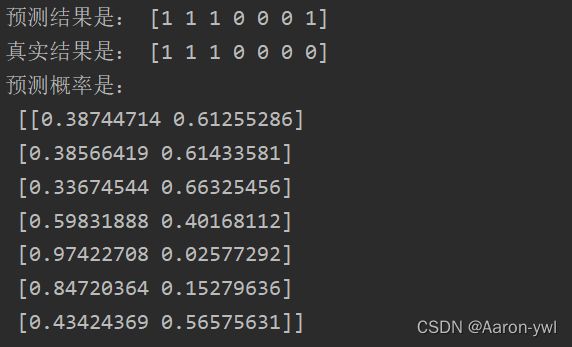
print('预测结果是:',y_pred)
print('真实结果是:',y_test)
# 计算概率,第一列为0的概率,第二列为1的概率
proba_ = model.predict_proba(X_test)
print('预测概率是:\n',proba_)