Python实现Logistc回归分类(西瓜数据集、鸢尾花数据集)详解
文章目录
- Logistic回归原理讲解
-
- 逻辑回归的损失函数
- 梯度下降
- 代码实现
-
- 西瓜数据集
-
- 全代码
- 鸢尾花(Iris)数据集
-
- LogisticModel
-
- 全代码
- 主函数实现
-
- 全代码
Logistic回归原理讲解
【声明】 笔者实验之前,参考了助教所提供的另一篇文章内容,自行又额外参考一篇CSDN中的相关文章,之后原理讲解将会基于此基础之上进行,引用其中部分内容进行讲解。
Logistic回归(LR):是一种常用的处理二分类问题的模型,二分类问题中,把结果y分成两个类,正类和负类。因变量y∈{0, 1},0是负类,1是正类。线性回归函数: f ( x ) = θ t x f(x) = \theta^tx f(x)=θtx的输出值在负无穷到正无穷的范围上,并不好区分是正类还是负类。因此引入非线性变换,把线性回归的输出值压缩到(0, 1)之间,Logistic回归就是通过使用Sigmoid函数,也称为逻辑函数(Logistic function) 进行非线性变换:
g ( z ) = 1 1 + e z g(z) = \frac{1}{1+e^z} g(z)=1+ez1
其函数图像如下:

不难看出Sigmoid函数成像为“S形,它的取值在[0, 1]之间,在远离0的地方函数的值会很快接近0或者1,它的这个特性对于解决二分类问题十分重要。将线性回归函数带入Sigmoid函数得到 g ( θ ) = 1 1 + e θ t x g(\theta) = \frac{1}{1+e^ { \theta^tx} } g(θ)=1+eθtx1
逻辑回归的损失函数
通常提到损失函数,我们不得不提到 代价函数(Cost Function) 及目标函数 (Object Function)。
损失函数(Loss Function) 直接作用于单个样本,用来表达样本的误差
代价函数(Cost Function) 是整个样本集的平均误差,对所有损失函数值的平均
目标函数(Object Function) 是我们最终要优化的函数,也就是代价函数+正则化函数(经验风险+结构风险)
概况来讲,任何能够衡量模型预测出来的值 h ( θ ) h(\theta) h(θ) 与真实值 y 之间的差异的函数都可以叫做代价函数 C ( θ ) C(\theta) C(θ)如果有多个样本,则可以将所有代价函数的取值求均值,记做 J ( θ ) J(\theta) J(θ) 。在逻辑回归中,最常用的是代价函数是交叉熵(Cross Entropy)函数,此时 J ( θ ) 和 C ( θ ) [ c o s t ( θ ) ] J(\theta)和C(\theta)[cost(\theta)] J(θ)和C(θ)[cost(θ)]如下:
c o s t ( θ ) = { − l o g ( h θ ( x ) ) y = 1 − l o g ( 1 − h θ ( x ) ) y = 0 cost(\theta)=\begin{equation} \left\{ \begin{array}{lr} -log(h_\theta(x))&y =1 \\ -log(1-h_\theta(x))&y=0 \end{array} \right. \end{equation} cost(θ)={−log(hθ(x))−log(1−hθ(x))y=1y=0
J ( θ ) = 1 m ∑ i = 1 m [ − y i l o g ( h θ ( x i ) ) − ( 1 − y i ) l o g ( 1 − h θ ( x i ) ) ] J(\theta) = \frac{1}{m}\sum\limits^m_{i=1}[-y^{i}log(h_\theta(x^i))-(1-y^i)log(1-h_\theta(x^i))] J(θ)=m1i=1∑m[−yilog(hθ(xi))−(1−yi)log(1−hθ(xi))]
有人可能会问为什么log之前要加负号呢?回忆之前提到的Sigmod函数的值域,只落在(0,1)之间,log在此时都为负数,所以负号用于保证值输出为正值。
梯度下降
我们更新迭代参数 θ \theta θ通过梯度下降的办法,通过对 J ( θ ) J(\theta) J(θ)求导,意在不断寻求最小的损失函数值,优化模型
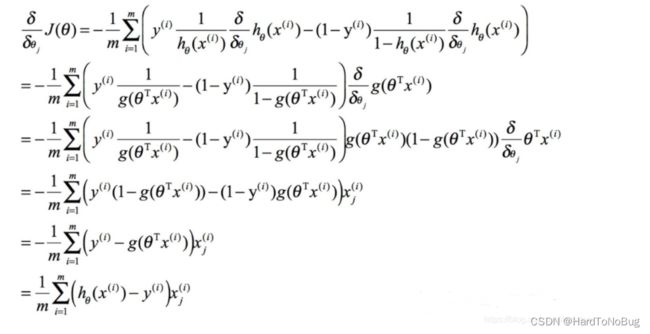
可得到
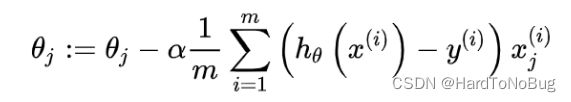
通过不断迭代即可更新学习参数
代码实现
西瓜数据集
实验的第一个部分是要求根据西瓜书上的西瓜数据集进行模型建立。具体其实只给了两个参数,分别是密度和含糖率,所以直接使用Logistic分类模型即可:
density = np.array([0.697, 0.774, 0.634, 0.608, 0.556, 0.403, 0.481, 0.437, 0.666,
0.243, 0.245, 0.343, 0.639, 0.657, 0.360, 0.593, 0.719]).reshape(-1, 1)
sugar_rate = np.array([0.460, 0.376, 0.264, 0.318, 0.215, 0.237, 0.149, 0.211, 0.091,
0.267, 0.057, 0.099, 0.161, 0.198, 0.370, 0.042, 0.103]).reshape(-1, 1)
在此我们先给出LogistcModel的初步定义:
class LogisticModel:
def __init__(self, X, Y, alpha=1, mini=0.0001) -> None:
self.x = X
self.y = Y
self.alpha = alpha#学习率
self.mini = mini#迭代停止最小误差
cnt = len(x[0]) #样本数量
self.theta = np.array([[0.0] for i in range(cnt)])
self.predict = [] #存放预测值
随后就是Sigmoid函数和损失函数的实现:
def __sigmoid(x):
return 1/(1 + np.exp(-x))
def __loss(self, theta):
# 计算损失值
sum = 0.0
for i in range(len(self.y)):
if y[i][0] == 1:
sum += - \
float(log(LogisticModel.__sigmoid(np.dot(x[i], theta))))
else:
sum += - \
float(log(1-LogisticModel.__sigmoid(np.dot(x[i], theta))))
return sum/len(self.y)
之后是编写梯度计算与循环检查函数:
def __gradient(self, theta):
# 求取梯度
sum = 0
for i in range(len(self.y)):
sum += (LogisticModel.__sigmoid(
float(np.dot(x[i], theta))) - y[i][0]) * x[i]
sum /= len(self.y)
ans = self.alpha*sum.reshape(-1, 1)
return ans
def __check(self):
# 检查是否达到迭代边界条件
TempOld = LogisticModel.__loss(self, self.theta)
Theta = LogisticModel.__gradient(self, self.theta)
self.theta -= Theta # 更新theta
TempNew = LogisticModel.__loss(self, self.theta)
result = abs((abs(TempNew)-abs(TempOld)))
if result <= self.mini:
return False
return True
def fit(self):
# 迭代梯度下降的过程
while(LogisticModel.__check(self)):
pass
最后的步骤就是对模型的预测与结果的输出,这里输出采用的是混淆矩阵(Confusion Matrix)
def predictSelf(self):
# 模型预测
for i in range(len(self.y)):
if(LogisticModel.__sigmoid(np.dot(self.x[i], self.theta)) > 0.5):
self.predict.append(1)
else:
self.predict.append(0)
def show(self, labels_name):
cm = (confusion_matrix(self.y.reshape(1, -1)[0], self.predict))
# 展示模型结果
print("accuracy:{:.2%}".format((cm[0][0]+cm[1][1])/(len(self.y))))
print("presicion:{:.2%}".format(cm[0][0]/(cm[0][0]+cm[0][1])))
print("recall:{:.2%}".format(cm[0][0]/(cm[0][0]+cm[1][0])))
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis] # 归一化
plt.imshow(cm, interpolation='nearest') # 在特定的窗口上显示图像
plt.title('WaterMelon') # 图像标题
plt.colorbar()
num_local = np.array(range(len(labels_name)))
plt.xticks(num_local, labels_name, rotation=90) # 将标签印在x轴坐标上
plt.yticks(num_local, labels_name) # 将标签印在y轴坐标上
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.show()
accuracy:82.35%
presicion:77.78%
recall:87.50%
全代码
这里额外解释一下,主函数中的x我是将Sugar_rate与density 合并在一起,y中记录的是真实值的数据。而C起初我是打算用作线性的函数常数项,但是随后发现引入C的准确率并不是很高,各位可以自己下去自行添加尝试。
import numpy as np
from numpy import log
from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
np.set_printoptions(suppress=True) # 取消科学计数法输出
class LogisticModel:
def __init__(self, X, Y, alpha=1, mini=0.0001) -> None:
self.x = X
self.y = Y
self.alpha = alpha
self.mini = mini
cnt = len(x[0])
self.theta = np.array([[0.0] for i in range(cnt)])
self.predict = []
def __sigmoid(x):
return 1/(1 + np.exp(-x))
def __loss(self, theta):
# 计算损失值
sum = 0.0
for i in range(len(self.y)):
if y[i][0] == 1:
sum += - \
float(log(LogisticModel.__sigmoid(np.dot(x[i], theta))))
else:
sum += - \
float(log(1-LogisticModel.__sigmoid(np.dot(x[i], theta))))
return sum/len(self.y)
def __gradient(self, theta):
# 求取梯度
sum = 0
for i in range(len(self.y)):
sum += (LogisticModel.__sigmoid(
float(np.dot(x[i], theta))) - y[i][0]) * x[i]
sum /= len(self.y)
ans = self.alpha*sum.reshape(-1, 1)
# print(theta - ans)
return ans
def __check(self):
# 检查是否达到迭代边界条件
TempOld = LogisticModel.__loss(self, self.theta)
Theta = LogisticModel.__gradient(self, self.theta)
self.theta -= Theta # 更新theta
TempNew = LogisticModel.__loss(self, self.theta)
result = abs((abs(TempNew)-abs(TempOld)))
if result <= self.mini:
return False
return True
def fit(self):
# 迭代梯度下降的过程
while(LogisticModel.__check(self)):
pass
def predictSelf(self):
# 模型预测
for i in range(len(self.y)):
if(LogisticModel.__sigmoid(np.dot(self.x[i], self.theta)) > 0.5):
self.predict.append(1)
else:
self.predict.append(0)
def show(self, labels_name):
cm = (confusion_matrix(self.y.reshape(1, -1)[0], self.predict))
# 展示模型结果
print("accuracy:{:.2%}".format((cm[0][0]+cm[1][1])/(len(self.y))))
print("presicion:{:.2%}".format(cm[0][0]/(cm[0][0]+cm[0][1])))
print("recall:{:.2%}".format(cm[0][0]/(cm[0][0]+cm[1][0])))
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis] # 归一化
plt.imshow(cm, interpolation='nearest') # 在特定的窗口上显示图像
plt.title('WaterMelon') # 图像标题
plt.colorbar()
num_local = np.array(range(len(labels_name)))
plt.xticks(num_local, labels_name, rotation=90) # 将标签印在x轴坐标上
plt.yticks(num_local, labels_name) # 将标签印在y轴坐标上
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.show()
density = np.array([0.697, 0.774, 0.634, 0.608, 0.556, 0.403, 0.481, 0.437, 0.666,
0.243, 0.245, 0.343, 0.639, 0.657, 0.360, 0.593, 0.719]).reshape(-1, 1)
sugar_rate = np.array([0.460, 0.376, 0.264, 0.318, 0.215, 0.237, 0.149, 0.211, 0.091,
0.267, 0.057, 0.099, 0.161, 0.198, 0.370, 0.042, 0.103]).reshape(-1, 1)
# 用于迭代Theta的常数项
C = np.array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1]).reshape(-1, 1)
#x = np.hstack((density, sugar_rate),C)
x = np.hstack((density, sugar_rate))
y = np.array([1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0,
0, 0, 0, 0, 0, 0]).reshape(-1, 1)
Test = LogisticModel(x, y)
Test.fit()
Test.predictSelf()
labels_name = ["good", "bad"]
Test.show(labels_name)
鸢尾花(Iris)数据集
鸢尾花数据集是一个多分类的数据集,获取方法可以看这篇文章
对于多分类的样本,显然不能直接使用Logistic模型对齐分类,这里介绍一种可以将二分类模型用于进行多分类的方法——投票法(VotingClassifier),以鸢尾花数据集为例,总共提供了3种不同类型的花,那么我们可以将之两两组合,形成3个分类器,预测时三个分类器分别预测其种类对其投票,票数多的即为预测结果,如果票数一致则可以任选一个种类记录:
LogisticModel
我的思路是首先对于之前的模型进行改造,使之可以适应鸢尾花的分类,
主要改变的其实就是画图的部分,去除了计算召回率和精确率(因为要分别对3个分类器求,过于繁杂),其次就是把title和混淆矩阵转移到函数外计算,
def show(cm, labels_name, title):
print("accuracy:{:.2%}".format(
(cm[0][0]+cm[1][1]+cm[2][2])/(np.sum(cm))))
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis] # 归一化
plt.imshow(cm, interpolation='nearest') # 在特定的窗口上显示图像
plt.title(title) # 图像标题
plt.colorbar()
num_local = np.array(range(len(labels_name)))
plt.xticks(num_local, labels_name, rotation=90) # 将标签印在x轴坐标上
plt.yticks(num_local, labels_name) # 将标签印在y轴坐标上
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.show()
还有就是对于梯度下降的界定条件由0.0001降低了一个百分比到0.001,原因是之后在我计算时,发现对于其中的一个模型来说,原先的精度会需要迭代更多的次数,有可能是深陷局部最小值难以跳出,加之降低精度后最终预测结果也可以接受,故改之。其实也可以改良梯度下降算法,例如:动量梯度下降法(gradient descent with momentum) 大家可以自行尝试
class LogisticModel:
def __init__(self, X, Y, alpha=1, mini=0.001) -> None:
self.x = X
self.y = Y
self.alpha = alpha
self.mini = mini
cnt = len(self.x[0])
self.theta = np.array([[0.0] for i in range(cnt)])
self.predict = []
全代码
import numpy as np
from numpy import log
import matplotlib.pyplot as plt
np.set_printoptions(suppress=True) # 取消科学计数法输出
class LogisticModel:
def __init__(self, X, Y, alpha=1, mini=0.001) -> None:
self.x = X
self.y = Y
self.alpha = alpha
self.mini = mini
cnt = len(self.x[0])
self.theta = np.array([[0.0] for i in range(cnt)])
self.predict = []
def sigmoid(x):
return 1/(1 + np.exp(-x))
def __loss(self, theta):
# 计算损失值
sum = 0.0
for i in range(len(self.y)):
if self.y[i][0] == 1:
sum += - \
float(log(LogisticModel.sigmoid(
np.dot(self.x[i], theta))))
else:
sum += - \
float(
log(1-LogisticModel.sigmoid(np.dot(self.x[i], theta))))
return sum/len(self.y)
def __gradient(self, theta):
# 求取梯度
sum = 0
for i in range(len(self.y)):
sum += (LogisticModel.sigmoid(
float(np.dot(self.x[i], theta))) - self.y[i][0]) * self.x[i]
sum /= len(self.y)
ans = self.alpha*sum.reshape(-1, 1)
# print(theta - ans)
return ans
def __check(self):
# 检查是否达到迭代边界条件
TempOld = LogisticModel.__loss(self, self.theta)
Theta = LogisticModel.__gradient(self, self.theta)
self.theta -= Theta # 更新theta
TempNew = LogisticModel.__loss(self, self.theta)
result = abs((abs(TempNew)-abs(TempOld)))
if result <= self.mini:
return False
return True
def fit(self):
# 迭代梯度下降的过程
while(LogisticModel.__check(self)):
pass
def predictSelf(self):
# 模型预测
for i in range(len(self.y)):
if(LogisticModel.sigmoid(np.dot(self.x[i], self.theta)) > 0.5):
self.predict.append(1)
else:
self.predict.append(0)
# def show_theta(self):
# print(self.theta)
def show(cm, labels_name, title):
print("accuracy:{:.2%}".format(
(cm[0][0]+cm[1][1]+cm[2][2])/(np.sum(cm))))
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis] # 归一化
plt.imshow(cm, interpolation='nearest') # 在特定的窗口上显示图像
plt.title(title) # 图像标题
plt.colorbar()
num_local = np.array(range(len(labels_name)))
plt.xticks(num_local, labels_name, rotation=90) # 将标签印在x轴坐标上
plt.yticks(num_local, labels_name) # 将标签印在y轴坐标上
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.show()
主函数实现
首先就是数据的读取和分类器的构建,这里我提供的标签训练值统一为前50位为1,后50位为0的列表,这是为了能够直接复用ModelLogistic类,回忆西瓜数据集时,我们正例标记为1,负例标记为0。这里相当于组合的前50类别标记为正,后50标记为负,因为鸢尾花的数据集十分规整,所以我们可以很轻易地将其分出3个类别。
Labels_name = ['SepalLength', 'SepalWidth',
'PetalLength', 'PetalWidth', 'Species']
# 读取表格数据
iris = pd.read_csv("D:\Code\python\Iris.csv", header=0, names=Labels_name)
x = np.hstack((np.array(iris[u'SepalLength']).reshape(-1, 1),
np.array(iris[u'SepalWidth']).reshape(-1, 1),
np.array(iris[u'PetalLength']).reshape(-1, 1),
np.array(iris[u'PetalWidth']).reshape(-1, 1)))
Y = np.hstack([[1]*50, [0]*50]).reshape(-1, 1)
x_SVer = np.vstack([x[0:50], x[50:100]])
x_VerVir = np.vstack([x[50:100], x[100:150]])
x_VirS = np.vstack([x[100:150], x[0:50]])
ModelA = LogisticModel(x_SVer, Y)
ModelB = LogisticModel(x_VerVir, Y)
ModelC = LogisticModel(x_VirS, Y)
ModelA.fit()
ModelB.fit()
ModelC.fit()
随后是编写投票器预测模型,免不了大量if语句:
def predict(a, b, c, test, pre):
for i in range(len(test)):
# 记票器
list = [0, 0, 0]
if(LogisticModel.sigmoid(np.dot(test[i], a.theta))) > 0.5:
list[0] += 1
else:
list[1] += 1
if(LogisticModel.sigmoid(np.dot(test[i], b.theta))) > 0.5:
list[1] += 1
else:
list[2] += 1
if(LogisticModel.sigmoid(np.dot(test[i], c.theta))) > 0.5:
list[2] += 1
else:
list[0] += 1
if(list[0] ^ list[1] ^ list[2] == 1):
pre.append("Iris-versicolor")
else:
if(list.index(2) == 0):
pre.append("Iris-setosa")
elif(list.index(2) == 1):
pre.append("Iris-versicolor")
elif(list.index(2) == 2):
pre.append("Iris-virginica")
这里的测试集需要我们自己划分,调用sklearn中的 train_test_split函数进行划分:
from sklearn.model_selection import train_test_split
y = np.array(iris[u'Species']).reshape(-1, 1) # 标签
x_train, x_test, y_train, y_test = train_test_split(
x, y, test_size=0.6) # 划分数据集
最后一步,预测+输出最终结果:
pre = [] # 存储预测结果
predict(ModelA, ModelB, ModelC, x_test, pre)
cm = (confusion_matrix(y_test, np.array(pre).reshape(-1, 1)))
print(cm)
title = "Iris Prediction"
LogisticModel.show(cm, ['setosa', 'versicolor', 'virginica'], title)
全代码
from LogisticModel import LogisticModel
import pandas as pd
import numpy as np
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
np.set_printoptions(suppress=True) # 取消科学计数法输出
def predict(a, b, c, test, pre):
for i in range(len(test)):
# 记票器
list = [0, 0, 0]
if(LogisticModel.sigmoid(np.dot(test[i], a.theta))) > 0.5:
list[0] += 1
else:
list[1] += 1
if(LogisticModel.sigmoid(np.dot(test[i], b.theta))) > 0.5:
list[1] += 1
else:
list[2] += 1
if(LogisticModel.sigmoid(np.dot(test[i], c.theta))) > 0.5:
list[2] += 1
else:
list[0] += 1
if(list[0] ^ list[1] ^ list[2] == 1):
pre.append("Iris-versicolor")
else:
if(list.index(2) == 0):
pre.append("Iris-setosa")
elif(list.index(2) == 1):
pre.append("Iris-versicolor")
elif(list.index(2) == 2):
pre.append("Iris-virginica")
Labels_name = ['SepalLength', 'SepalWidth',
'PetalLength', 'PetalWidth', 'Species']
# 读取表格数据
iris = pd.read_csv("D:\Code\python\Iris.csv", header=0, names=Labels_name)
x = np.hstack((np.array(iris[u'SepalLength']).reshape(-1, 1),
np.array(iris[u'SepalWidth']).reshape(-1, 1),
np.array(iris[u'PetalLength']).reshape(-1, 1),
np.array(iris[u'PetalWidth']).reshape(-1, 1)))
Y = np.hstack([[1]*50, [0]*50]).reshape(-1, 1)
x_SVer = np.vstack([x[0:50], x[50:100]])
x_VerVir = np.vstack([x[50:100], x[100:150]])
x_VirS = np.vstack([x[100:150], x[0:50]])
ModelA = LogisticModel(x_SVer, Y)
ModelB = LogisticModel(x_VerVir, Y)
ModelC = LogisticModel(x_VirS, Y)
ModelA.fit()
ModelB.fit()
ModelC.fit()
y = np.array(iris[u'Species']).reshape(-1, 1) # 标签
x_train, x_test, y_train, y_test = train_test_split(
x, y, test_size=0.6) # 划分数据集
pre = [] # 存储预测结果
predict(ModelA, ModelB, ModelC, x_test, pre)
cm = (confusion_matrix(y_test, np.array(pre).reshape(-1, 1)))
print(cm)
title = "Iris Prediction"
LogisticModel.show(cm, ['setosa', 'versicolor', 'virginica'], title)


