[论文阅读]Range-Focused Fusion of Camera-IMU-UWB for Accuarte and Drift Reduced Localization
Range-Focused Fusion of Camera-IMU-UWB for Accuarte and Drift Reduced Localization
摘要
在这项工作中,提出了一个单目相机、6自由度IMU和一个UWB锚的紧耦合融合方案以实现精确和减少漂移的定位。
具体来说,这项工作着重于将超宽带传感器纳入现有的最先进的视觉惯性系统。
之前针对这一目标的研究使用一个最近的超宽带距离数据来更新机器人在滑动窗口中的位置(位置聚焦),并展示了较好的结果。
然而,(1)这些方法忽略了超宽带与相机传感器之间的时间偏移;(2)两个连续关键帧之间的所有其他范围。
本文的方法通过利用视觉惯性里程管道中现成的传播信息,将视角转移到超宽带测量(距离聚焦)。这允许一更有效的方式使用超宽带数据:处理每个范围数据的时间偏移,并可以利用所有可用的测量。
实验结果表明,该方法在估计锚点位置和减少长期轨迹漂移方面均优于以往的方法。
I. Introduction
VINS-SLAM、OpenVINS都能提供非常精确和高速率的姿态与速度估计,但传感器噪声和计算误差使系统容易随着时间的推移而累积漂移,目前累积漂移问题流行的解决方案是包括一个额外的全局传感器。
松耦合:即首先在分离的定位系统中计算UWB和相机-IMU数据,然后将UWB和相机-IMU子系统获得的位置估计进行对齐和融合。
只使用未知位置的单一超宽带锚的方法。这种系统既具有无漂移范围测量的优点,可以用来精确定位,又便于实际应用,因为不需要设置时间来校准锚点的位置。结果表明,通过将超宽带,相机和IMU测量进行紧耦合在一个联合优化问题中,可以实现更精确和稳健的定位。
然而,这些方法以类似模拟的方式处理超宽带数据:每个相机位置与一个距离测量配对,而两个连续相机帧之间的任何其他距离都不考虑,由于许多原因,这个视角不能反映现实生活中的传感器系统:
- 真实的UWB传感器独立于相机和IMU传感器,因此在距离图像信息之间总是会有时间偏移;
- UWB距离测量速率不符合标准相机或IMU速率,UWB数据速率往往比相机高几倍,在实际操作中,由于失去视线,UWB数据速率可能会变化,这意味着可用的UWB数据量也可能变化。
为了解决上述问题,论文利用VIO管道中现有的状态传播过程,为每个距离数据高效地制定UWB误差项,主要贡献如下:
- 所谓的“距离聚焦”视角,通过利用VIO管道计算的传播数据来处理超宽带测量,这充分解决了UWB相机传感器之间的时间偏移,并允许所有可用的超宽带数据被消耗;
- 一个单目相机、一个6自由度IMU和一个UWB锚提供漂移减少里程计的紧耦合融合方案,内置一个UWB锚定位模块来估计未知锚点位置;
- 大量的实验结果来验证每个提出的uwb辅助系统组件的性能。
II. LITERATURE REVIEW
A. UWB辅助定位和映射
获得唯一的3D距离定位解决方案需要:
1)至少4个已知位置的UWB锚定,或
2)3个已知锚定和机器人[24],[25]的高度数据。
这种假设限制了系统的适用场景,因为操作区域需要适应超宽带锚定装置的设置,而且每个新环境都需要额外的时间和精力来校准锚定装置的位置。
为了缓解这一需求,最近的方法尝试在操作过程中估计锚点地图,因为机器人可以获得带有额外锚点间范围[23]的度量距离,或者仅获得带有额外锚点间范围[15]、[22]的度量距离,甚至只有[17]、[18]的尺度距离。
然而,这些解决方案仍然以次优的方式处理超宽带数据,这在第II-B节中解释。
在这项工作中,我们探索了相机- imu和超宽带的组合,只有一个锚在一个未知的位置。这种设置结合了VIO管道的优点,可以实现精确的短期里程测量和最灵活的超宽带锚定配置。
B. 视觉惯性测距定位与测绘
与这项工作最相关的是使用相机- IMU-UWB传感器定位和测绘任务的作品。
虽然大多数方法都采用VIO进行板载定位,并分别使用UWB进行基于距离的相对定位[26]-[29],但最近的研究表明,可以融合视觉、惯性和UWB数据,同时获得锚点位置估计和改进姿态估计,[15]提出了EKF解决方案,[14]采用了姿态图优化框架。
虽然最终目标和融合方法不同,但这些方法使用超宽带数据的基本原则是相同的:残差是从状态向量中的位置角度制定的。该视图导致以下问题:
1)一个位置与一个最近的超宽带测量配对,忽略相机帧和距离数据之间的时间偏移;
2)两个连续相机帧之间的所有其他范围被丢弃。
相比之下,所提出的系统根据距离测量的时间戳来计算超宽带残差,这使得距离数据可以在传感器的精度下使用。通过利用VIO管道中IMU状态传播过程的结果,导出了每个距离测量的超宽带残差,从而考虑了时间偏移问题,并可以利用所有可用的范围。
III. PRELIMINARIES
A. 系统概述
图2说明了拟议系统的概览。一个移动机器人配备了一个单目相机,一个6自由度IMU和一个超宽带传感器刚性附着在身体框架上,所有的内外参数都经过校准。距离测量到一个单一的超宽带锚放置在一个未知的位置是可用的。在这项工作中,采用双向飞行时间(TW-ToF)超宽带传感器,因为它不需要传感器之间的时钟同步,因此更适合于许多应用场景。
该系统分两个阶段运作:
(1)基于VIO的超宽带锚定定位(章节IV-B):最初仅使用摄像机和IMU提供精确的短期里程计,并结合距离测量来估计超宽带锚定位置。当不确定度低于某一阈值时,锚点位置估计被认为是固定的。
(2)视觉-惯性-距离里程计(IV-C部分):一旦找到超宽带锚点位置,后续的距离测量将与视觉和惯性数据紧密融合在一起,以联合基于关键帧的优化,获得精确的和漂移减少的长期里程数。
理论上,这两个阶段可以合并为一个阶段(即通过UWB锚点位置扩展VIO优化的状态矢量)。然而,由于多种原因,这种规则在实践中不太可能奏效:
- VIO的滑动窗口只能包含较短的时间跨度的数据,这不利于超宽带定位任务,因为超宽带定位任务对三维空间位置数据的依赖性很强。扩展窗口大小是不可行的,因为视觉测量的指数增长将给计算机带来巨大的计算负担。
- 如果不提供锚点位置的良好初始猜测,优化将难以产生任何令人满意的结果。由于这个初始猜测通常是手动测量的,并且可能会随着每次操作而改变,因此它容易受到人为错误的影响,应该避免。
B. 符号说明
图1(a)所示为本文所使用的坐标系,包括IMU坐标系对应的刚体坐标系 B {B} B、相机坐标系 C {C} C和世界坐标系 W {W} W。
齐次变换矩阵 T ∈ S E ( 3 ) T∈SE(3) T∈SE(3)由旋转矩阵 A R ^AR AR和位置向量 A p ^Ap Ap组成,表示帧 a {a} a中的一个三维姿态:
A R ^AR AR的四元数表示是 A q = [ q x , q y , q z , q w ] T ^Aq = [q_x, q_y, q_z, q_w]^T Aq=[qx,qy,qz,qw]T( q w q_w qw是标量部分)。
我们在计算时使用 A T ^AT AT的 紧致 形式为 [ A p T , A q T ] T [^Ap^T,^Aq^T]^T [ApT,AqT]T。
t c t_c tc、 t i t_i ti、 t j t_j tj分别表示相机的时间戳,IMU、UWB距离测量。
T k T_k Tk是滑动窗口中一个关键帧的时间戳,不会失一般性它被设置为 t k = : t c t_k =: t_c tk=:tc。
应该注意的是,只有在满足某些标准[1]的情况下,相机帧才被选择为关键帧。
这可以导致两个连续的关键帧被多个相机帧分开。
因此,两个关键帧之间的UWB测量数据在滑动窗口内往往不均匀。图1(b)展示了这一观察结果的一个例子。
C. 基于优化的单目视觉惯性里程计
滑动窗口 X X X由视觉特征状态 X L X_L XL和IMU状态 X B X_B XB组成:( X X X可以视为位姿和速度向量)
其中 K K K为关键帧的个数。在 t k t_k tk时刻,IMU的每个状态 x k x_k xk由IMU在世界坐标系中的位置、姿态、速度以及加速度计和陀螺仪在体坐标系中的偏差组成。
VIO管道使用BA公式,最小化损失函数:
包括视觉残差 e v n , m e_{v}^{n,m} evn,m, IMU残差 e i k e^k_i eik和边缘残差 e p e_p ep[30]。
C C C是在第 n n n帧和第 m m m帧中观察到的地标集合。
∣ ∣ ∗ ∣ ∣ ||*|| ∣∣∗∣∣表示向量的欧氏范数。
对视觉残差采用Huber范数 ρ ρ ρ[31]来减小异常点跟踪的影响。
D.IMU状态传播
IMU预积分方法[32]允许利用IMU从 t i t_i ti到 t i + 1 t_i+1 ti+1的测量值将高频线加速度和角速度预积分为伪测量 α i + 1 i α^i_{i+1} αi+1i, β i + 1 i β^i_{i+1} βi+1i, γ i + 1 i γ^i_{i+1} γi+1i[1]。
这些项分别对应于预积分惯性和相对定向测量。每次在 t k t_k tk创建一个新的关键帧时,所有传播的状态都被重置:
对于 t i + 1 t_{i+1} ti+1处后续的每一个新的IMU测量,状态按照公式(5)递归传播:
生成IMU-rate状态估计值。利用这个操作,在 t j t_j tj当一个新的范围测量被接收 ( t j > t k ) (t_j > t_k) (tj>tk),传播状态 ( B W p j ^ , B W v j ^ , B W q j ^ ) (^W_B\widehat{p_j}, ^W_B\widehat{v_j}, ^W_B\widehat{q_j}) (BWpj ,BWvj ,BWqj ) 是现成的。由此,基于IMU对世界坐标系中 t k t_k tk到 t j t_j tj位置变化的预测简化为:
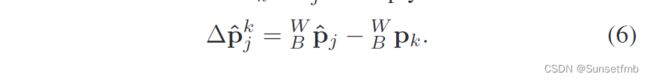
IV. Camera-IMU-UWB的距离聚焦融合
在本节中,我们介绍了这项工作的主要贡献,从“距离聚焦”的超宽带残差的制定,到实现超宽带锚定定位和基于关键帧的视觉-惯性-距离测距。
A.位置聚焦 vs.距离聚焦UWB残差
图1(a-b)显示了相机和超宽带测量之间的时间偏移示例。 e r e_r er为UWB残差。在之前的著作中 e r e_r er的公式(例如,[14],[15],[33]),在本文中被称为“位置聚焦”,将滑动窗口 B W p k ^W_Bp_k BWpk中的每个位置与最近时间戳的一个范围测量关联起来:
但是,这种提法没有考虑到第II-B节所讨论的实际问题。在这项工作中,我们提出了所谓的“距离聚焦”公式,它将每个距离数据与相同时间戳的位置关联起来:( d j d_j dj表示机器人到UWB锚点的测量距离)
通过调整位置到每个距离数据在 t j ( B W p j ) t_j(^W_Bp_j) tj(BWpj),进一步的解释在第IV-B和IV-C节。
如果同时满足下列条件 ( Δ t j = t j − t k ) (Δt_j = t_j−t_k) (Δtj=tj−tk),可以认为(7)和(8)是相同的:
1) B W p k ^W_Bp_k BWpk和 d j d_j dj之间没有时间偏移 ( Δ t j = 0 ) (Δt_j = 0) (Δtj=0),即相机和UWB传感器是同步的,和
2)要么UWB和相机传感器有相同的数据速率或两个相机帧之间的所有其他额外的距离测量被忽略。
事实上,仿真(Section V-A)表明,在这些条件下,两种公式有相似的结果。
然而,在现实中,摄像机和超宽带传感器总是相互独立工作,因此时间偏移问题是固有的,不应该被忽视。
此外,标准的超宽带数据速率往往比相机的高很多倍。
因此,以前的方法总是会丢弃相当一部分可用的距离数据,这意味着超宽带传感器仍然没有得到充分利用。
B.基于VIO数据的超宽带锚定
1)问题公式化:
使用短期精确VIO数据(位姿和速度)估计世界坐标系内的超宽带锚定位置 W a p ^Wap Wap(图1(a)),我们在数据窗口上制定了一个优化问题:
其由VIO管道的里程计数据和相应的IMU速率输出位置 B W p j ^ ^W_B\widehat{p_j} BWpj 组成。
图3概述了可以作为一个独立系统开发的模块。需要最小化的损失函数为
用 ρ ρ ρ表示Huber损失。方程中引入的超宽带残差 e r j e^j_r erj(8),可以用IMU-rate的位置来计算
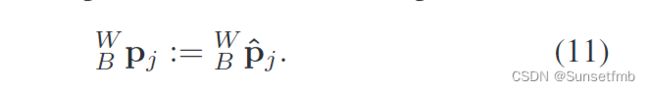
我们注意到,对于具有噪声IMU数据的低成本系统,IMU-rate状态传播可能是不可靠的。因此, B W p j ^W_Bp_j BWpj可以从更稳定的相机速率状态估计计算为 B W p j : = B W p k + B W v k Δ t j ^W_Bp_j:=^W_Bp_k + ^W_Bv_kΔt_j BWpj:=BWpk+BWvkΔtj。
2)充分条件:
在[29]中已经建立了问题的可观察性,说明机器人不应该直接向锚移动。
在实际应用中,估计结果取决于覆盖所有三维轴的轨迹,以及锚点相对于运动半径的距离。
S x 2 S^2_x Sx2表示 x x x轴上位置的样本方差( y y y轴和 z z z轴类似),当机器人移动时,每一个新的位置数据都会递归更新。
为保证优化的性能,将检查以下条件,启动或跳过优化过程:
- ‖ B W v j ^ ‖ > v m i n ‖^W_B\hat{v_j}‖> v_{min} ‖BWvj^‖>vmin: 检查机器人是否在移动,因为如果机器人是静态的,新数据将是相同的,优化结果不会得到改善,
- min S x y z 2 > S m i n 2 \min S^2_{xyz} > S^2_{min} minSxyz2>Smin2: 检查每个轴位置的样本方差是否足够大,即机器人的运动覆盖所有方向,
其中 v m i n v_{min} vmin和 S m i n 2 S^2_{min} Smin2是用户定义的参数。对于每个新的VIO数据都要检查第一个条件,直到满足终止条件(章节IV-B3)。
对第二个条件进行检查,直到第一次满足为止。
通过施加这些条件,我们发现,通过毫不费力地初始猜测锚点位置( a W p 0 = [ 0 , 0 , 0 ] T ^W_ap_0 =[0,0,0]^T aWp0=[0,0,0]T),估计可以获得令人满意的结果,这是我们所有实验中的设置。但是,良好的初始猜测可以提高收敛时间,在实践中可以考虑提高性能。
3)终止准则:
一旦启动,可以使用标准Levenberg-Marquardt算法[34]和Ceres解算器[35]对代价函数(10)进行优化。由于系统是在线执行的,因此引入终止判据来确定解的不确定度:

以 σ m a x σ_{max} σmax为协方差矩阵的最大奇异值, σ p σ_p σp为给定的阈值。一旦满足该准则,就完成了UWB锚定位操作,并确定了 a W p ^W_ap aWp。
图4是收敛的一个例子。由于 σ m a x σ_{max} σmax的计算不是必需的,但由于秩不足检查和雅可比矩阵的求逆可能会很耗时,因此终止检查可以在单独的线程中以较慢的速度运行(例如每10个新的UWB范围)。
因此,优化可能会额外运行几次,但处理时间不会受到影响。
C. 基于关键帧的视觉-惯性-距离里程计
1)问题公式化:
一旦找到超宽带锚定位置,摄像头-IMU-超宽带传感器可以紧密融合,提供更稳健、准确和漂移减少的里程数。
为此,我们建议将仅VI的代价函数 E V I ( χ ) E_{VI}\left(χ\right) EVI(χ)(3)与“范围聚焦”的超宽带残差(8)扩大,以形成整体代价函数:
式中 J k J_k Jk为滑动窗口中 t k t_k tk和 t k + 1 t_{k+1} tk+1两个关键帧之间的距离数据集以及相应的位置预测变化(由式6计算):
图1(c-d)描述了与以前的“位置聚焦”方法相比,所提系统的因子图。 J k J_k Jk中的测量值用于创建连接到状态 x k x_k xk的超宽带因子。超宽带残差由一个预先定义的 γ r γ_r γr因子重新加权,以放大其对优化的影响。接下来,根据(8)的主要思想,通过修改来提高性能,得到了超宽带剩余 e r j e^j_r erj。
2)距离聚焦超宽带因子(Range-Focused UWB Factor):
t j t_j tj时刻的位置可以通过以下一种方法关联到状态 x k x_k xk:
使用(16),仅基于IMU数据( Δ p j k ^ Δ\hat{p^k_j} Δpjk^,从(6)计算)从VIO管道传播的位置用于预测任意时间戳的位置。
然而,由于只有一个位置状态( B W p k ^W_Bp_k BWpk)与多个UWB测量直接相关,该解决方案可能会过拟合到有噪声的UWB或IMU数据。
另一方面,使用(17)允许位置( B W p k ^W_Bp_k BWpk)和速度( B W v k ^W_Bv_k BWvk)状态与距离测量相耦合。
尽管如此,匀速模型可能不适合灵活机动,特别是当 Δ t j Δt_j Δtj可能比两个相机帧之间的周期更长。
在这项工作中,我们提出(16)和(17)结合,既利用基于IMU数据的预测,又利用运动模型:
遵循VINS-Mono[1]边缘化策略,每当该关键帧被边缘化时,连接到第一帧的超宽带因子与视觉因子和惯性因子一起转化为线性化的先验.
V. EXPERIMENTAL RESULTS
对每个模块(IV-B和IV-C)分别进行了实际实验和仿真评估。比较主要是在提议的“范围聚焦”方法和以前的“位置聚焦”方法之间进行的,以VINS-Mono的结果作为改善访问的基线。
A.超宽带锚定定位
首先,我们只评估UWB锚定定位组件与现实生活中的实验。该硬件包括一个英特尔Realsense T265摄像头,可提供30hz的立体图像,200hz的IMU数据和38hz的超宽带数据,来自两个独立锚点(没有锚点间范围),距离起始位置2m。
地面真实轨迹由Vicon系统提供。系统运行在VIO-only模式(使用左摄像头和IMU数据测程,不涉及超宽带)。利用估计锚点位置 e p e_p ep的距离误差进行比较。
实验是针对两个锚点进行的,每个锚点的位置估计是在不同的线程中进行的,以避免相互影响。
图5说明了同时估计两个锚点的结果。两种方法的最终误差均小于0.1 m,但可以看出本文方法的收敛速度要快得多。
这是因为我们的“距离聚焦”方法提高了每一个新的距离测量的解决方案,而“位置聚焦”对应的对象在收集足够的数据来取得突破之前,被困在一个局部最小值。
通过仿真来验证和比较:
1)超宽带与相机数据之间的时间偏移,
2)到锚点的距离(da)相对于轨迹“半径”(rb),以及
3)超宽带数据频率相对于相机数据频率的效果。
图6(a)显示了仿真设置。位置和速度数据在20hz产生,一个超宽带锚提供20hz的距离数据。所有数据被 η ∼ N ( 0 , 0.02 ) η\sim N(0, 0.02) η∼N(0,0.02)的高斯噪声破坏。
每次仿真都进行估计,直到满足Levenberg-Marquardt算法的停止准则。如果满足条件(12),我们停止模拟,得到锚的位置估计和位置误差。否则,估计将继续下一个数据点,并使用最终的估计来测量误差。
首先,通过提供相同的超宽带和位置数据,但不同的时间偏移(0-37.5 ms)来验证时间偏移的影响。图6(b-c)分别显示了之前和本文提出的方法的结果。
其次,在相同的时间偏移37.5 ms和其他设置下,我们评估了增加超宽带数据频率的性能。图6(d)显示了我们的方法的结果。
先前的“位置聚焦”方法不使用额外的超宽带数据,因此不包括在内。
从图6(b-d)所示的结果可以看出:
-
当时间偏移量增加时,“位置聚焦”方法会受到影响(图6(b)),而“距离聚焦”方法总是表现良好(图6©)。
-
另一方面,当没有时间抵消时,这两种公式的性能是与另一种相同的,这将遵循第四节- a的分析。对于两种方法,随着UWB锚点放置距离机器人越远,误差越大(图6(b-c))。但是,由于所提方法的误差不受时间偏移的影响,因此更有利于实际应用。
-
然而,当超宽带速率增加时,系统的性能并没有明显的改善(图6(d))。对于这个任务,结果强烈依赖于大的移动和锚相对接近,以达到理想的结果。
B . Visual-Inertial-Range测程法
采用绝对轨迹误差(ATE)评价系统的测程性能,是评价SLAM系统[36]的标准方法。在计算绝对位姿差来计算整体ATE之前,首先对估计轨迹和地面真轨迹进行对齐
1)使用EuRoC数据集模拟:
对于EuRoC数据集,在SLAM帧的起点模拟一个超宽带锚点。我们按照VIR-SLAM[14]的描述来确保模拟设置是相同的,以便进行比较。由于所有的“MH”序列开始与手持式自举运动,超宽带锚位置是在实际飞行前估计。
随着两个连续关键帧之间的可用范围的数量增加,随着更多的相机帧被跳过,直到一个新的关键帧,对于大多数序列,我们有 ∣ J k ∣ ≈ 2 − 4 |J_k|≈2−4 ∣Jk∣≈2−4(相机和模拟超宽带具有相同的数据频率20 Hz)。
在表I中,完整的拟议系统对应于“Any ∣ J k ∣ |J_k| ∣Jk∣”列(使用了所有可用范围)。我们通过限制与一个关键帧( ∣ J k ∣ = 1 , 2 |J_k| = 1,2 ∣Jk∣=1,2)相关的最大距离测量次数来进一步评估该系统。图7描绘了一些估计轨迹和地面真实轨迹。
![[论文阅读]Range-Focused Fusion of Camera-IMU-UWB for Accuarte and Drift Reduced Localization_第14张图片](http://img.e-com-net.com/image/info8/0db7af32b4c24c0c8b3c428dee9e6e05.jpg)
从表一可以清楚地看出,尽管VIR-SLAM(一种具有复杂公式的“位置聚焦”方法)改进了原来的VINS-Mono,但当只使用相同数量的距离测量时( ∣ J k ∣ = 1 |J_k| = 1 ∣Jk∣=1),我们的方法表现更好。
随着越来越多的距离可用,该系统甚至得到进一步增强。然而,在某些情况下,当包含更多的范围数据时,ATE的改进很小,这表明更多的超宽带数据并不一定保证性能的提高。
此外,还对可用于“距离聚焦”超宽带残差(8)的其他 B W p j ^W_Bp_j BWpj公式进行了测试。所选的解决方案(18)在所有数据集中都超过了基于IMU的(16)和基于模型的(17)预测,而在(16)和(17)之间,在性能方面没有明显的区别。
表2报告了ATE结果。比较了T265 VI-SLAM(立体相机+ IMU), VINS-Mono(单声道相机+ IMU),我们对“位置聚焦”系统的实现和提出的“距离聚焦”方法(单目相机+ IMU +一个超宽带锚)。
图8显示了Loop_02数据集的轨迹概况和位置误差的均方根(RMS)。
对于视觉惯性方法(VINS-Mono和T265 VI-SLAM),累积漂移没有随着时间的推移进行校正,导致了更大的误差。
当采用“定位聚焦”方法处理超宽带数据时,性能明显提高。然而,所提出的解决方案显然优于所有的实验。
VI. CONCLUSION
本文提出了一种新的“距离聚焦”的相机- imu - uwb传感器融合方法。
我们利用VIO系统中现成的传播数据来补偿UWB和相机传感器之间的时间偏移,并允许使用所有可用的UWB数据。
这一想法被整合到两个UWB辅助组件中:一个UWB锚定定位模块和一个基于紧密耦合优化的视觉-惯性-距离数据融合,以在长期作业中提供精确的、减少漂移的里程数。
对于这两个部件,实际实验和模拟实验结果都验证了所提出的系统优于先前的“位置聚焦”方法。
向多机器人场景扩展是未来的主要研究方向。
具体来说,我们希望利用机器人之间的测距数据,不仅可以改进每个系统的里程数,还可以组合不共享任何公共视觉循环闭包的单个地图。
![[论文阅读]Range-Focused Fusion of Camera-IMU-UWB for Accuarte and Drift Reduced Localization_第1张图片](http://img.e-com-net.com/image/info8/d1387cd732bf40f9b1cb7f5c0afdc6f4.jpg)
![[论文阅读]Range-Focused Fusion of Camera-IMU-UWB for Accuarte and Drift Reduced Localization_第2张图片](http://img.e-com-net.com/image/info8/f805afe67a57488296184516829da044.jpg)
![[论文阅读]Range-Focused Fusion of Camera-IMU-UWB for Accuarte and Drift Reduced Localization_第3张图片](http://img.e-com-net.com/image/info8/4346b5e5dbb749f6be913d5a9ae6e44e.jpg)
![[论文阅读]Range-Focused Fusion of Camera-IMU-UWB for Accuarte and Drift Reduced Localization_第4张图片](http://img.e-com-net.com/image/info8/ad794c0d9df84f0f9ec2a05e3cdc45b0.jpg)
![[论文阅读]Range-Focused Fusion of Camera-IMU-UWB for Accuarte and Drift Reduced Localization_第5张图片](http://img.e-com-net.com/image/info8/5be530bdc0ea4cb7af8bfdeb23dbf634.jpg)

![[论文阅读]Range-Focused Fusion of Camera-IMU-UWB for Accuarte and Drift Reduced Localization_第6张图片](http://img.e-com-net.com/image/info8/ae141f74c3204b4bb13543f6fdb3d879.jpg)
![[论文阅读]Range-Focused Fusion of Camera-IMU-UWB for Accuarte and Drift Reduced Localization_第7张图片](http://img.e-com-net.com/image/info8/08bfa328b0ce413a8e54a69b288d3a04.jpg)
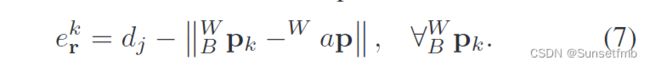

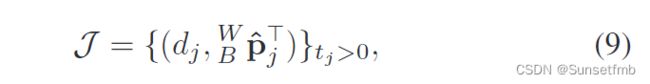
![[论文阅读]Range-Focused Fusion of Camera-IMU-UWB for Accuarte and Drift Reduced Localization_第8张图片](http://img.e-com-net.com/image/info8/f6c1ac311afa4936ac431e05cf657d0c.jpg)
![[论文阅读]Range-Focused Fusion of Camera-IMU-UWB for Accuarte and Drift Reduced Localization_第9张图片](http://img.e-com-net.com/image/info8/5d65f4601e7d4eb0919e06bcb06d7299.jpg)
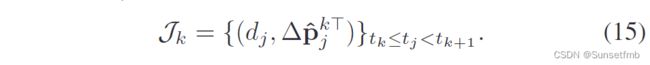
![[论文阅读]Range-Focused Fusion of Camera-IMU-UWB for Accuarte and Drift Reduced Localization_第10张图片](http://img.e-com-net.com/image/info8/49a468bb3c2f4508a4f3b7e35040c7c5.jpg)
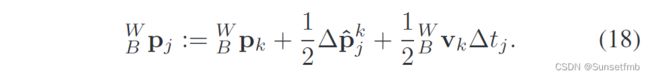
![[论文阅读]Range-Focused Fusion of Camera-IMU-UWB for Accuarte and Drift Reduced Localization_第11张图片](http://img.e-com-net.com/image/info8/94b7742dd5634f93868b6f781e4acdd6.jpg)
![[论文阅读]Range-Focused Fusion of Camera-IMU-UWB for Accuarte and Drift Reduced Localization_第12张图片](http://img.e-com-net.com/image/info8/11cb9cf5b8be4433bc1ba68193012d31.jpg)
![[论文阅读]Range-Focused Fusion of Camera-IMU-UWB for Accuarte and Drift Reduced Localization_第13张图片](http://img.e-com-net.com/image/info8/990539cc13524530bea9f0795f3a7757.jpg)
![[论文阅读]Range-Focused Fusion of Camera-IMU-UWB for Accuarte and Drift Reduced Localization_第15张图片](http://img.e-com-net.com/image/info8/d8de03ebe90342809963e7eb053a66a2.jpg)
![[论文阅读]Range-Focused Fusion of Camera-IMU-UWB for Accuarte and Drift Reduced Localization_第16张图片](http://img.e-com-net.com/image/info8/8b98963ce6564efcbdab91f6f0f55bfe.jpg)