【李代数求偏导】SLAM中李代数SE3求偏导左扰动模型和右扰动模型的区别
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 前言
- 结论
-
- 1、左扰动模型:
- 2、右扰动模型:
-
- 2.1右扰动+右乘更新
- 2.2右扰动+左乘更新
- 3、将T展开后求偏导(具体看后文)
-
- 3.1右扰动+右乘更新
- 3.2左扰动+左乘更新
- 一、利用左扰动模型求雅可比矩阵
- 二、利用右扰动模型求雅可比矩阵
-
- 2.1 右扰动模型+右乘更新
- 2.2右扰动模型+左乘更新
-
- 三、把T展开后求Jacobin
- 3.1右扰动+右乘更新
- 3.2左扰动+左乘更新
前言
在学习SLAM的过程中,我一直对用左扰动模型和右扰动模型求SE3的偏导有疑惑,好奇他们的计算结果有什么区别。本文用《SLAM十四讲》ch7的实验验证了两者的差别。另外推荐一篇知乎上讲的不错的文章。
http://www-quic.zhihu.com/question/454486535
结论
首先放出实验结果,共分为两组:
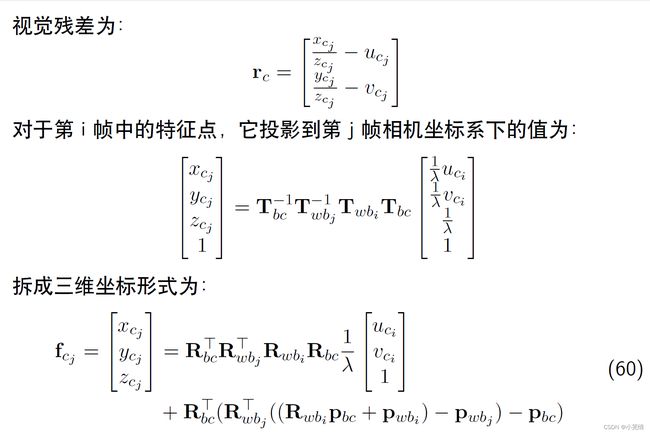
实验求解的问题是 P c i = T c w P w i = R c w f w i + t Pci=TcwPwi=Rcwfwi+t Pci=TcwPwi=Rcwfwi+t
其中 P c 为 i 时刻特征点在相机坐标系的坐标, P w 为 i 时刻特征点在世界坐标系下的坐标 Pc为i时刻特征点在相机坐标系的坐标, Pw为i时刻特征点在世界坐标系下的坐标 Pc为i时刻特征点在相机坐标系的坐标,Pw为i时刻特征点在世界坐标系下的坐标
这里我们采用左扰动模型在给定EPNP计算结果为初始值的情况下的优化结果为参考,计算各种方法的误差大小
1、左扰动模型:
用EPNP计算初始值并进行优化的结果如下
因为以其自身为参考,精度转化产生了误差(实际应该为0),这里误差小不代表左扰动就好,只是那它本身作为标准而已。(不太严谨请见谅)。
与左扰动优化的姿态误差 dR=4.76555e-07
与左扰动优化的位置误差 dt=2.12013e-07
与EPNP姿态误差 dR=0.00238751
与EPNP位置误差 dt=0.00283737
初始值为零直接进行优化的结果如下:
与左扰动优化的姿态误差 dR=2.75866
与左扰动优化的位置误差 dt=3.57404
与EPNP姿态误差 dR=2.75899
与EPNP位置误差 dt=3.57507
2、右扰动模型:
2.1右扰动+右乘更新
用EPNP计算初始值并进行优化的结果如下
与左扰动优化的姿态误差 dR=8.57513e-05
与左扰动优化的位置误差 dt=8.69039e-05
与EPNP姿态误差 dR=0.00245202
与EPNP位置误差 dt=0.00292116
初始值为零直接进行优化的结果如下:
与左扰动优化的姿态误差 dR=2.79226
与左扰动优化的位置误差 dt=3.01685
与EPNP姿态误差 dR=1.73205
与EPNP位置误差 dt=2.94471
2.2右扰动+左乘更新
用EPNP计算初始值并进行优化的结果如下
与左扰动优化的姿态误差 dR=7.07704e-05
与左扰动优化的位置误差 dt=6.83382e-05
与EPNP姿态误差 dR=0.00242649
与EPNP位置误差 dt=0.00288342
初始值为零直接进行优化的结果如下:
与左扰动优化的姿态误差 dR=2.82814
与左扰动优化的位置误差 dt=0.141753
与EPNP姿态误差 dR=2.82817
与EPNP位置误差 dt=0.140666
3、将T展开后求偏导(具体看后文)
3.1右扰动+右乘更新
用EPNP计算初始值并进行优化的结果如下
与左扰动优化的姿态误差 dR=9.14896e-05
与左扰动优化的位置误差 dt=9.07626e-05
与EPNP姿态误差 dR=0.00245898
与EPNP位置误差 dt=0.00292396
初始值为零直接进行优化的结果如下:
与左扰动优化的姿态误差 dR=2.82832
与左扰动优化的位置误差 dt=0.172576
与EPNP姿态误差 dR=2.82833
与EPNP位置误差 dt=0.170768
3.2左扰动+左乘更新
用EPNP计算初始值并进行优化的结果如下
与左扰动优化的姿态误差 dR=6.46337e-05
与左扰动优化的位置误差 dt=5.86872e-05
与EPNP姿态误差 dR=0.00243119
与EPNP位置误差 dt=0.00288491
初始值为零直接进行优化的结果如下:
与左扰动优化的姿态误差 dR=2.78006
与左扰动优化的位置误差 dt=2.59136
与EPNP姿态误差 dR=2.78033
与EPNP位置误差 dt=2.59216
一、利用左扰动模型求雅可比矩阵
根据《SLAM十四讲》里的左扰动求导可知:
 其g2o库中的线性化的函数
其g2o库中的线性化的函数linearizeOplus()如下:详细对比可以发现与书中的公式是一一对应的。
// 这是g2o官方库中的代码,/home/jxl/software/g2o/g2o/types/sba/types_six_dof_expmap.cpp
void EdgeProjectXYZ2UV::linearizeOplus() {
VertexSE3Expmap * vj = static_cast<VertexSE3Expmap *>(_vertices[1]);
SE3Quat T(vj->estimate());
VertexSBAPointXYZ* vi = static_cast<VertexSBAPointXYZ*>(_vertices[0]);
Vector3D xyz = vi->estimate();
Vector3D xyz_trans = T.map(xyz);
double x = xyz_trans[0];
double y = xyz_trans[1];
double z = xyz_trans[2];
double z_2 = z*z;
const CameraParameters * cam = static_cast<const CameraParameters *>(parameter(0));
Matrix<double,2,3,Eigen::ColMajor> tmp;
tmp(0,0) = cam->focal_length;
tmp(0,1) = 0;
tmp(0,2) = -x/z*cam->focal_length;
tmp(1,0) = 0;
tmp(1,1) = cam->focal_length;
tmp(1,2) = -y/z*cam->focal_length;
_jacobianOplusXi = -1./z * tmp * T.rotation().toRotationMatrix();
_jacobianOplusXj(0,0) = x*y/z_2 *cam->focal_length;
_jacobianOplusXj(0,1) = -(1+(x*x/z_2)) *cam->focal_length;
_jacobianOplusXj(0,2) = y/z *cam->focal_length;
_jacobianOplusXj(0,3) = -1./z *cam->focal_length;
_jacobianOplusXj(0,4) = 0;
_jacobianOplusXj(0,5) = x/z_2 *cam->focal_length;
_jacobianOplusXj(1,0) = (1+y*y/z_2) *cam->focal_length;
_jacobianOplusXj(1,1) = -x*y/z_2 *cam->focal_length;
_jacobianOplusXj(1,2) = -x/z *cam->focal_length;
_jacobianOplusXj(1,3) = 0;
_jacobianOplusXj(1,4) = -1./z *cam->focal_length;
_jacobianOplusXj(1,5) = y/z_2 *cam->focal_length;
}
用EPNP计算初始值并进行优化的结果如下:
-- Max dist : 94.000000
-- Min dist : 4.000000
一共找到了79组匹配点
3d-2d pairs: 75
R=
[0.9979059095501264, -0.05091940089110115, 0.03988747043654633;
0.0498186625425323, 0.998362315743816, 0.02812094175376019;
-0.04125404886078842, -0.02607491352883862, 0.9988083912027648]
t=
[-0.1267821389558076;
-0.008439496817513407;
0.06034935748888434]
calling bundle adjustment
iteration= 0 chi2= 0.001139 time= 0.000299452 cumTime= 0.000299452 edges= 75 schur= 1 lambda= 78.084078 levenbergIter= 1
iteration= 1 chi2= 0.000000 time= 4.3151e-05 cumTime= 0.000342603 edges= 75 schur= 1 lambda= 52.056052 levenbergIter= 1
iteration= 2 chi2= 0.000000 time= 4.1157e-05 cumTime= 0.00038376 edges= 75 schur= 1 lambda= 34.704035 levenbergIter= 1
iteration= 3 chi2= 0.000000 time= 3.9925e-05 cumTime= 0.000423685 edges= 75 schur= 1 lambda= 23.136023 levenbergIter= 1
iteration= 4 chi2= 0.000000 time= 3.9655e-05 cumTime= 0.00046334 edges= 75 schur= 1 lambda= 15.424015 levenbergIter= 1
iteration= 5 chi2= 0.000000 time= 3.9454e-05 cumTime= 0.000502794 edges= 75 schur= 1 lambda= 10.282677 levenbergIter= 1
iteration= 6 chi2= 0.000000 time= 0.000139251 cumTime= 0.000642045 edges= 75 schur= 1 lambda= 224628.504738 levenbergIter= 6
iteration= 7 chi2= 0.000000 time= 9.2594e-05 cumTime= 0.000734639 edges= 75 schur= 1 lambda= 230019588.851357 levenbergIter= 4
optimization costs time: 0.00132516 seconds.
after optimization:
T=
0.997848 -0.0510879 0.0410952 -0.128454
0.0499059 0.998324 0.0292911 -0.0103276
-0.0425228 -0.0271772 0.998726 0.0590494
0 0 0 1
与左扰动优化的姿态误差 dR=4.76555e-07
与左扰动优化的位置误差 dt=2.12013e-07
与EPNP姿态误差 dR=0.00238751
与EPNP位置误差 dt=0.00283737
初始值为零直接进行优化的结果如下:
-- Max dist : 94.000000
-- Min dist : 4.000000
一共找到了79组匹配点
3d-2d pairs: 75
R=
[0, 0, 0;
0, 0, 0;
0, 0, 0]
t=
[0;
0;
0]
calling bundle adjustment
iteration= 0 chi2= 2491379.880686 time= 0.000143138 cumTime= 0.000143138 edges= 75 schur= 1 lambda= 155.465777 levenbergIter= 1
iteration= 1 chi2= 713797.506230 time= 4.1999e-05 cumTime= 0.000185137 edges= 75 schur= 1 lambda= 103.643851 levenbergIter= 1
iteration= 2 chi2= 258277.050045 time= 4.0386e-05 cumTime= 0.000225523 edges= 75 schur= 1 lambda= 69.095901 levenbergIter= 1
iteration= 3 chi2= 7554.374159 time= 4.0296e-05 cumTime= 0.000265819 edges= 75 schur= 1 lambda= 23.031967 levenbergIter= 1
iteration= 4 chi2= 11.920051 time= 4.0566e-05 cumTime= 0.000306385 edges= 75 schur= 1 lambda= 7.677322 levenbergIter= 1
iteration= 5 chi2= 0.000028 time= 3.9915e-05 cumTime= 0.0003463 edges= 75 schur= 1 lambda= 2.559107 levenbergIter= 1
iteration= 6 chi2= 0.000000 time= 3.9694e-05 cumTime= 0.000385994 edges= 75 schur= 1 lambda= 1.706072 levenbergIter= 1
iteration= 7 chi2= 0.000000 time= 3.9223e-05 cumTime= 0.000425217 edges= 75 schur= 1 lambda= 1.137381 levenbergIter= 1
iteration= 8 chi2= 0.000000 time= 3.9424e-05 cumTime= 0.000464641 edges= 75 schur= 1 lambda= 0.758254 levenbergIter= 1
iteration= 9 chi2= 0.000000 time= 4.9954e-05 cumTime= 0.000514595 edges= 75 schur= 1 lambda= 0.505503 levenbergIter= 1
iteration= 10 chi2= 0.000000 time= 3.8973e-05 cumTime= 0.000553568 edges= 75 schur= 1 lambda= 0.337002 levenbergIter= 1
iteration= 11 chi2= 0.000000 time= 3.9274e-05 cumTime= 0.000592842 edges= 75 schur= 1 lambda= 0.224668 levenbergIter= 1
iteration= 12 chi2= 0.000000 time= 0.00012803 cumTime= 0.000720872 edges= 75 schur= 1 lambda= 4907.944462 levenbergIter= 6
iteration= 13 chi2= 0.000000 time= 5.6696e-05 cumTime= 0.000777568 edges= 75 schur= 1 lambda= 6543.925950 levenbergIter= 2
iteration= 14 chi2= 0.000000 time= 5.6817e-05 cumTime= 0.000834385 edges= 75 schur= 1 lambda= 8725.234600 levenbergIter= 2
iteration= 15 chi2= 0.000000 time= 3.9153e-05 cumTime= 0.000873538 edges= 75 schur= 1 lambda= 5816.823067 levenbergIter= 1
iteration= 16 chi2= 0.000000 time= 7.4379e-05 cumTime= 0.000947917 edges= 75 schur= 1 lambda= 31023.056355 levenbergIter= 3
iteration= 17 chi2= 0.000000 time= 3.9614e-05 cumTime= 0.000987531 edges= 75 schur= 1 lambda= 62046.112709 levenbergIter= 1
optimization costs time: 0.00208049 seconds.
after optimization:
T=
0.959118 0.0610826 -0.276336 0.965119
0.167898 -0.908845 0.381852 -0.613753
-0.227822 -0.412637 -0.881946 -3.28965
0 0 0 1
与左扰动优化的姿态误差 dR=2.75866
与左扰动优化的位置误差 dt=3.57404
与EPNP姿态误差 dR=2.75899
与EPNP位置误差 dt=3.57507
二、利用右扰动模型求雅可比矩阵
右扰动模型的雅可比推导如下:
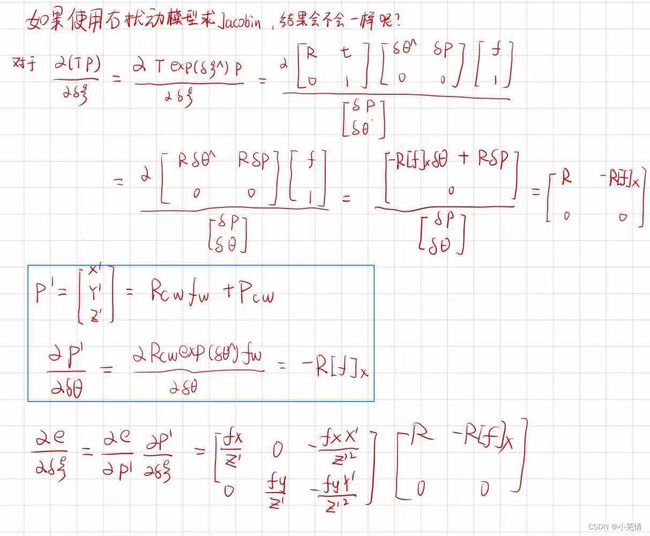
这里代码的处理稍微复杂一点,首先我们需要把g2o官方库中的 EdgeProjectXYZ2UV 单独提出了,我们就命名为 MyEdgeProjectXYZ2UV ,除了linearizeOplus()函数不一样,其他都一样。下面我们修改linearizeOplus()函数:
void MyEdgeProjectXYZ2UV::linearizeOplus() {
MyVertexSE3Expmap * vj = static_cast<MyVertexSE3Expmap *>(_vertices[1]);
SE3Quat T(vj->estimate());
VertexSBAPointXYZ* vi = static_cast<VertexSBAPointXYZ*>(_vertices[0]);
Vector3D xyz = vi->estimate();
Vector3D xyz_trans = T.map(xyz);
double x = xyz_trans[0];
double y = xyz_trans[1];
double z = xyz_trans[2];
double z_2 = z*z;
const CameraParameters * cam = static_cast<const CameraParameters *>(parameter(0));
Eigen::Matrix<double,2,3,Eigen::ColMajor> tmp;
tmp(0,0) = cam->focal_length;
tmp(0,1) = 0;
tmp(0,2) = -x/z*cam->focal_length;
tmp(1,0) = 0;
tmp(1,1) = cam->focal_length;
tmp(1,2) = -y/z*cam->focal_length;
Eigen::Matrix3d tmp_R = T.rotation().toRotationMatrix();
_jacobianOplusXi = -1./z * tmp * T.rotation().toRotationMatrix();
Eigen::Matrix<double,3,6,Eigen::ColMajor> tmp_p;
//右扰动
Eigen::Matrix3d tmp_fx;
tmp_fx << 0, -xyz[2], xyz[1], xyz[2], 0, -xyz[0], -xyz[1], xyz[0], 0;
tmp_p.block(0, 0, 3, 3) = -tmp_R * tmp_fx;//对姿态的雅可比 = -R[p]^
tmp_p.block(0, 3, 3, 3) = tmp_R;//对位置的雅可比 = R
//左扰动
// Eigen::Matrix3d tmp_fx;
// tmp_fx << 0.0, -xyz_trans[2], xyz_trans[1], xyz_trans[2], 0.0, -xyz_trans[0], -xyz_trans[1], xyz_trans[0], 0.0;
// tmp_p.block(0, 0, 3, 3) = -tmp_fx;//对姿态的雅可比 = -R[p]^
// tmp_p.block(0, 3, 3, 3) = Eigen::Matrix3d::Identity(3, 3);//对位置的雅可比 = R
Eigen::Matrix<double,2,6,Eigen::ColMajor> jres = (-1./z * tmp * tmp_p);
_jacobianOplusXj = jres;
除了修改linearizeOplus()函数, 对于待优化姿态变量的更新我们同样需要修改为右乘(右扰动模型),具体做法与上述类似,将官方库中的 VertexSE3Expmap 提取出来,并修改 oplusImpl()函数。同时我们对比,不修改使用左乘更新和使用右乘更新二者的区别。
virtual void oplusImpl(const double* update_) {
Eigen::Map<const Vector6d> update(update_);
setEstimate(SE3Quat::exp(update)*estimate());
}
2.1 右扰动模型+右乘更新
提供EPNP初始值的情况下,输出结果为:
-- Max dist : 94.000000
-- Min dist : 4.000000
一共找到了79组匹配点
3d-2d pairs: 75
R=
[0.9979059095501264, -0.05091940089110115, 0.03988747043654633;
0.0498186625425323, 0.998362315743816, 0.02812094175376019;
-0.04125404886078842, -0.02607491352883862, 0.9988083912027648]
t=
[-0.1267821389558076;
-0.008439496817513407;
0.06034935748888434]
calling bundle adjustment
iteration= 0 chi2= 0.000959 time= 0.000131485 cumTime= 0.000131485 edges= 75 schur= 1 lambda= 71.408604 levenbergIter= 1
iteration= 1 chi2= 0.000000 time= 4.3151e-05 cumTime= 0.000174636 edges= 75 schur= 1 lambda= 47.605736 levenbergIter= 1
iteration= 2 chi2= 0.000000 time= 4.0185e-05 cumTime= 0.000214821 edges= 75 schur= 1 lambda= 31.737157 levenbergIter= 1
iteration= 3 chi2= 0.000000 time= 4.0486e-05 cumTime= 0.000255307 edges= 75 schur= 1 lambda= 21.158105 levenbergIter= 1
iteration= 4 chi2= 0.000000 time= 4.0565e-05 cumTime= 0.000295872 edges= 75 schur= 1 lambda= 14.105403 levenbergIter= 1
iteration= 5 chi2= 0.000000 time= 4.0496e-05 cumTime= 0.000336368 edges= 75 schur= 1 lambda= 9.403602 levenbergIter= 1
iteration= 6 chi2= 0.000000 time= 4.0376e-05 cumTime= 0.000376744 edges= 75 schur= 1 lambda= 6.269068 levenbergIter= 1
iteration= 7 chi2= 0.000000 time= 0.000133589 cumTime= 0.000510333 edges= 75 schur= 1 lambda= 136949.883156 levenbergIter= 6
iteration= 8 chi2= 0.000000 time= 4.0345e-05 cumTime= 0.000550678 edges= 75 schur= 1 lambda= 91299.922104 levenbergIter= 1
iteration= 9 chi2= 0.000000 time= 5.0985e-05 cumTime= 0.000601663 edges= 75 schur= 1 lambda= 60866.614736 levenbergIter= 1
iteration= 10 chi2= 0.000000 time= 4.0776e-05 cumTime= 0.000642439 edges= 75 schur= 1 lambda= 121733.229472 levenbergIter= 1
optimization costs time: 0.00125543 seconds.
after optimization:
T=
0.997848 -0.0510535 0.0411376 -0.128522
0.0498693 0.998325 0.0293161 -0.0103714
-0.0425654 -0.0272015 0.998723 0.0590173
0 0 0 1
与左扰动优化的姿态误差 dR=8.57513e-05
与左扰动优化的位置误差 dt=8.69039e-05
与EPNP姿态误差 dR=0.00245202
与EPNP位置误差 dt=0.00292116
不提供初始值(初始值为0)的情况下:
-- Max dist : 94.000000
-- Min dist : 4.000000
一共找到了79组匹配点
3d-2d pairs: 75
R=
[0, 0, 0;
0, 0, 0;
0, 0, 0]
t=
[0;
0;
0]
calling bundle adjustment
iteration= 0 chi2= 2491379.880680 time= 0.00026826 cumTime= 0.00026826 edges= 75 schur= 1 lambda= 155.465777 levenbergIter= 1
iteration= 1 chi2= 1195376.724224 time= 4.4303e-05 cumTime= 0.000312563 edges= 75 schur= 1 lambda= 103.643851 levenbergIter= 1
iteration= 2 chi2= 524300.404187 time= 4.2079e-05 cumTime= 0.000354642 edges= 75 schur= 1 lambda= 69.095901 levenbergIter= 1
iteration= 3 chi2= 32476.786520 time= 4.1277e-05 cumTime= 0.000395919 edges= 75 schur= 1 lambda= 23.031967 levenbergIter= 1
iteration= 4 chi2= 106.158049 time= 4.1027e-05 cumTime= 0.000436946 edges= 75 schur= 1 lambda= 7.677322 levenbergIter= 1
iteration= 5 chi2= 0.000036 time= 4.1387e-05 cumTime= 0.000478333 edges= 75 schur= 1 lambda= 2.559107 levenbergIter= 1
iteration= 6 chi2= 0.000000 time= 4.0916e-05 cumTime= 0.000519249 edges= 75 schur= 1 lambda= 1.706072 levenbergIter= 1
iteration= 7 chi2= 0.000000 time= 4.0606e-05 cumTime= 0.000559855 edges= 75 schur= 1 lambda= 1.137381 levenbergIter= 1
iteration= 8 chi2= 0.000000 time= 4.0666e-05 cumTime= 0.000600521 edges= 75 schur= 1 lambda= 0.758254 levenbergIter= 1
iteration= 9 chi2= 0.000000 time= 4.0285e-05 cumTime= 0.000640806 edges= 75 schur= 1 lambda= 0.505503 levenbergIter= 1
iteration= 10 chi2= 0.000000 time= 0.000133599 cumTime= 0.000774405 edges= 75 schur= 1 lambda= 11042.875040 levenbergIter= 6
iteration= 11 chi2= 0.000000 time= 4.0445e-05 cumTime= 0.00081485 edges= 75 schur= 1 lambda= 7361.916694 levenbergIter= 1
iteration= 12 chi2= 0.000000 time= 4.0095e-05 cumTime= 0.000854945 edges= 75 schur= 1 lambda= 4907.944462 levenbergIter= 1
iteration= 13 chi2= 0.000000 time= 4.0395e-05 cumTime= 0.00089534 edges= 75 schur= 1 lambda= 3271.962975 levenbergIter= 1
iteration= 14 chi2= 0.000000 time= 4.1607e-05 cumTime= 0.000936947 edges= 75 schur= 1 lambda= 6543.925950 levenbergIter= 1
optimization costs time: 0.00189716 seconds.
after optimization:
T=
0.981512 0.18784 0.0367605 0.302452
0.168669 -0.939616 0.29778 -0.45664
0.0904756 -0.286074 -0.953926 -2.89333
0 0 0 1
与左扰动优化的姿态误差 dR=2.79226
与左扰动优化的位置误差 dt=3.01685
与EPNP姿态误差 dR=1.73205
与EPNP位置误差 dt=2.94471
2.2右扰动模型+左乘更新
提供EPNP初始值的情况下,输出结果为:
-- Max dist : 94.000000
-- Min dist : 4.000000
一共找到了79组匹配点
3d-2d pairs: 75
R=
[0.9979059095501264, -0.05091940089110115, 0.03988747043654633;
0.0498186625425323, 0.998362315743816, 0.02812094175376019;
-0.04125404886078842, -0.02607491352883862, 0.9988083912027648]
t=
[-0.1267821389558076;
-0.008439496817513407;
0.06034935748888434]
calling bundle adjustment
iteration= 0 chi2= 0.214111 time= 0.000119923 cumTime= 0.000119923 edges= 75 schur= 1 lambda= 71.408604 levenbergIter= 1
iteration= 1 chi2= 0.001222 time= 4.3211e-05 cumTime= 0.000163134 edges= 75 schur= 1 lambda= 23.802868 levenbergIter= 1
iteration= 2 chi2= 0.000015 time= 5.2938e-05 cumTime= 0.000216072 edges= 75 schur= 1 lambda= 15.868579 levenbergIter= 1
iteration= 3 chi2= 0.000000 time= 4.1568e-05 cumTime= 0.00025764 edges= 75 schur= 1 lambda= 10.579052 levenbergIter= 1
iteration= 4 chi2= 0.000000 time= 4.1016e-05 cumTime= 0.000298656 edges= 75 schur= 1 lambda= 7.052702 levenbergIter= 1
iteration= 5 chi2= 0.000000 time= 4.1007e-05 cumTime= 0.000339663 edges= 75 schur= 1 lambda= 4.701801 levenbergIter= 1
iteration= 6 chi2= 0.000000 time= 4.1227e-05 cumTime= 0.00038089 edges= 75 schur= 1 lambda= 3.134534 levenbergIter= 1
iteration= 7 chi2= 0.000000 time= 4.0436e-05 cumTime= 0.000421326 edges= 75 schur= 1 lambda= 2.089689 levenbergIter= 1
iteration= 8 chi2= 0.000000 time= 4.0866e-05 cumTime= 0.000462192 edges= 75 schur= 1 lambda= 1.393126 levenbergIter= 1
iteration= 9 chi2= 0.000000 time= 4.0906e-05 cumTime= 0.000503098 edges= 75 schur= 1 lambda= 0.928751 levenbergIter= 1
iteration= 10 chi2= 0.000000 time= 4.0476e-05 cumTime= 0.000543574 edges= 75 schur= 1 lambda= 0.619167 levenbergIter= 1
iteration= 11 chi2= 0.000000 time= 4.0526e-05 cumTime= 0.0005841 edges= 75 schur= 1 lambda= 0.412778 levenbergIter= 1
iteration= 12 chi2= 0.000000 time= 4.0566e-05 cumTime= 0.000624666 edges= 75 schur= 1 lambda= 0.275185 levenbergIter= 1
iteration= 13 chi2= 0.000000 time= 4.0856e-05 cumTime= 0.000665522 edges= 75 schur= 1 lambda= 0.183457 levenbergIter= 1
iteration= 14 chi2= 0.000000 time= 4.0806e-05 cumTime= 0.000706328 edges= 75 schur= 1 lambda= 0.122305 levenbergIter= 1
iteration= 15 chi2= 0.000000 time= 0.000135002 cumTime= 0.00084133 edges= 75 schur= 1 lambda= 2671.785558 levenbergIter= 6
iteration= 16 chi2= 0.000000 time= 4.0897e-05 cumTime= 0.000882227 edges= 75 schur= 1 lambda= 1781.190372 levenbergIter= 1
iteration= 17 chi2= 0.000000 time= 4.0826e-05 cumTime= 0.000923053 edges= 75 schur= 1 lambda= 1187.460248 levenbergIter= 1
iteration= 18 chi2= 0.000000 time= 9.6951e-05 cumTime= 0.00102 edges= 75 schur= 1 lambda= 1215959.293810 levenbergIter= 4
optimization costs time: 0.00223933 seconds.
after optimization:
T=
0.997848 -0.0510589 0.041136 -0.128521
0.0498758 0.998326 0.029291 -0.0103273
-0.0425627 -0.0271763 0.998724 0.0590352
0 0 0 1
与左扰动优化的姿态误差 dR=7.07704e-05
与左扰动优化的位置误差 dt=6.83382e-05
与EPNP姿态误差 dR=0.00242649
与EPNP位置误差 dt=0.00288342
不提供初始值(初始值为0)的情况下:
-- Max dist : 94.000000
-- Min dist : 4.000000
一共找到了79组匹配点
3d-2d pairs: 75
R=
[0, 0, 0;
0, 0, 0;
0, 0, 0]
t=
[0;
0;
0]
calling bundle adjustment
iteration= 0 chi2= 5545636.870216 time= 0.000435984 cumTime= 0.000435984 edges= 75 schur= 1 lambda= 8401867357611196416.000000 levenbergIter= 10
optimization costs time: 0.000627261 seconds.
after optimization:
T=
1 0 0 0
0 -1 0 0
0 0 -1 0
0 0 0 1
与左扰动优化的姿态误差 dR=2.82814
与左扰动优化的位置误差 dt=0.141753
与EPNP姿态误差 dR=2.82817
与EPNP位置误差 dt=0.140666
三、把T展开后求Jacobin
为什么会对比这种方法呢?因为在《手写VIO》的课程中,他们是先将f展开成旋转矩阵+平移的形式,并对姿态和位置分别求导。
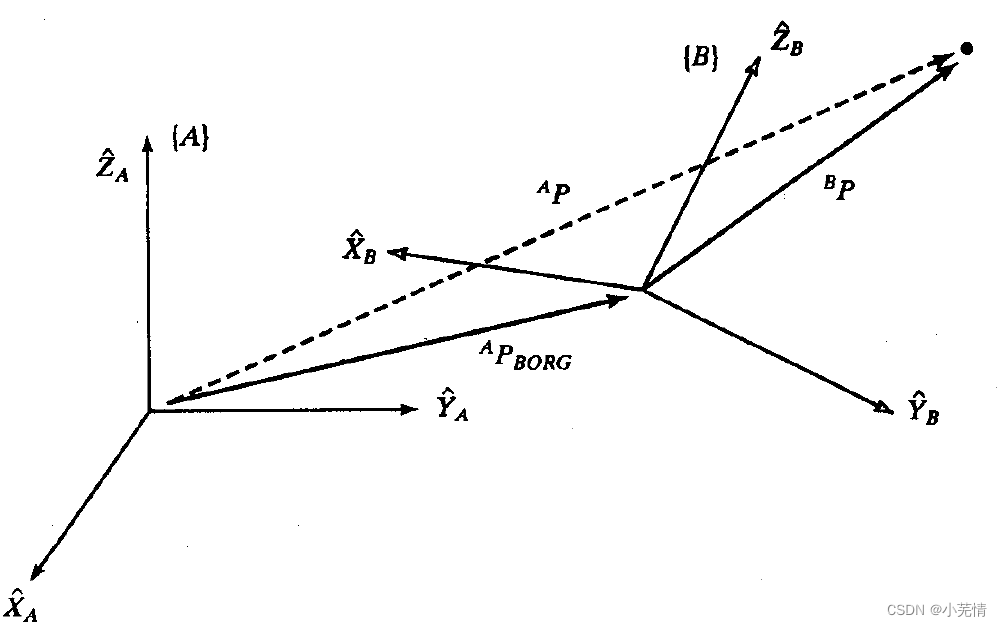
也就是说,在我们上述讨论的模型(即SLAM十四讲中ch7的PNP模型)中,我们先将相机坐标系下特征点坐标展开 P ‘ = T c w ∗ P w = R c w ∗ f w + t P^`=Tcw*Pw=Rcw*fw+t P‘=Tcw∗Pw=Rcw∗fw+t其中 f w = [ X , Y , Z ] fw=[X,Y,Z] fw=[X,Y,Z]即特征点在世界坐标系下的坐标。
可以看到展开后无论是右扰动还是左扰动,都是与原来有一定差别的,或是在姿态上,或是在平移上,具体为什么产生这样的差异我还没弄太清楚。但是想想一个坐标系B相对于坐标系A运动,经过δt时间后,坐标系B的姿态变化了δa,位置变化了δb(即右扰动模型),如果对于位置的雅可比为单位矩阵,那么位置不应该发生变化。但是实际情况是 P A B P^{AB} PAB随姿态R不同而发生改变。这也解释了为什么前面求位置雅可比为R。
下面我们仍然进行实验,用数据说话:
3.1右扰动+右乘更新
代码只需要修改MyEdgeProjectXYZ2UV::linearizeOplus()函数中对于位置的导数。
tmp_p.block(0, 3, 3, 3) = Eigen::Matrix3d::Identity(3,3);
提供EPNP初始值的情况下,输出结果为:
-- Max dist : 94.000000
-- Min dist : 4.000000
一共找到了79组匹配点
3d-2d pairs: 75
R=
[0.9979059095501264, -0.05091940089110115, 0.03988747043654633;
0.0498186625425323, 0.998362315743816, 0.02812094175376019;
-0.04125404886078842, -0.02607491352883862, 0.9988083912027648]
t=
[-0.1267821389558076;
-0.008439496817513407;
0.06034935748888434]
calling bundle adjustment
iteration= 0 chi2= 0.153981 time= 0.00222382 cumTime= 0.00222382 edges= 75 schur= 1 lambda= 71.408604 levenbergIter= 1
iteration= 1 chi2= 0.000885 time= 4.4784e-05 cumTime= 0.00226861 edges= 75 schur= 1 lambda= 23.802868 levenbergIter= 1
iteration= 2 chi2= 0.000002 time= 4.1207e-05 cumTime= 0.00230981 edges= 75 schur= 1 lambda= 15.868579 levenbergIter= 1
iteration= 3 chi2= 0.000000 time= 4.0796e-05 cumTime= 0.00235061 edges= 75 schur= 1 lambda= 10.579052 levenbergIter= 1
iteration= 4 chi2= 0.000000 time= 4.0666e-05 cumTime= 0.00239128 edges= 75 schur= 1 lambda= 7.052702 levenbergIter= 1
iteration= 5 chi2= 0.000000 time= 4.0515e-05 cumTime= 0.00243179 edges= 75 schur= 1 lambda= 4.701801 levenbergIter= 1
iteration= 6 chi2= 0.000000 time= 4.0295e-05 cumTime= 0.00247209 edges= 75 schur= 1 lambda= 3.134534 levenbergIter= 1
iteration= 7 chi2= 0.000000 time= 4.0296e-05 cumTime= 0.00251238 edges= 75 schur= 1 lambda= 2.089689 levenbergIter= 1
iteration= 8 chi2= 0.000000 time= 4.0335e-05 cumTime= 0.00255272 edges= 75 schur= 1 lambda= 1.393126 levenbergIter= 1
iteration= 9 chi2= 0.000000 time= 4.0306e-05 cumTime= 0.00259302 edges= 75 schur= 1 lambda= 0.928751 levenbergIter= 1
iteration= 10 chi2= 0.000000 time= 4.0496e-05 cumTime= 0.00263352 edges= 75 schur= 1 lambda= 0.619167 levenbergIter= 1
iteration= 11 chi2= 0.000000 time= 4.0456e-05 cumTime= 0.00267397 edges= 75 schur= 1 lambda= 0.412778 levenbergIter= 1
iteration= 12 chi2= 0.000000 time= 4.0265e-05 cumTime= 0.00271424 edges= 75 schur= 1 lambda= 0.275185 levenbergIter= 1
iteration= 13 chi2= 0.000000 time= 4.0526e-05 cumTime= 0.00275477 edges= 75 schur= 1 lambda= 0.183457 levenbergIter= 1
iteration= 14 chi2= 0.000000 time= 0.000152374 cumTime= 0.00290714 edges= 75 schur= 1 lambda= 256491.413538 levenbergIter= 7
iteration= 15 chi2= 0.000000 time= 5.9101e-05 cumTime= 0.00296624 edges= 75 schur= 1 lambda= 341988.551384 levenbergIter= 2
iteration= 16 chi2= 0.000000 time= 9.6972e-05 cumTime= 0.00306321 edges= 75 schur= 1 lambda= 350196276.617265 levenbergIter= 4
optimization costs time: 0.00423397 seconds.
after optimization:
T=
0.997848 -0.0510522 0.0411351 -0.128518
0.0498677 0.998325 0.0293259 -0.0103897
-0.0425634 -0.0272115 0.998723 0.0590331
0 0 0 1
与左扰动优化的姿态误差 dR=9.14896e-05
与左扰动优化的位置误差 dt=9.07626e-05
与EPNP姿态误差 dR=0.00245898
与EPNP位置误差 dt=0.00292396
不提供初始值(初始值为0)的情况下:
-- Max dist : 94.000000
-- Min dist : 4.000000
一共找到了79组匹配点
3d-2d pairs: 75
R=
[0, 0, 0;
0, 0, 0;
0, 0, 0]
t=
[0;
0;
0]
calling bundle adjustment
iteration= 0 chi2= 5484482.653301 time= 0.000167523 cumTime= 0.000167523 edges= 75 schur= 1 lambda= 326035364.127842 levenbergIter= 7
iteration= 1 chi2= 5411109.314310 time= 2.9485e-05 cumTime= 0.000197008 edges= 75 schur= 1 lambda= 217356909.418561 levenbergIter= 1
iteration= 2 chi2= 5333174.533993 time= 2.8423e-05 cumTime= 0.000225431 edges= 75 schur= 1 lambda= 144904606.279041 levenbergIter= 1
iteration= 3 chi2= 5266555.302930 time= 2.8012e-05 cumTime= 0.000253443 edges= 75 schur= 1 lambda= 96603070.852694 levenbergIter= 1
iteration= 4 chi2= 5234122.025044 time= 3.8953e-05 cumTime= 0.000292396 edges= 75 schur= 1 lambda= 64402047.235129 levenbergIter= 1
iteration= 5 chi2= 5232554.289042 time= 5.2639e-05 cumTime= 0.000345035 edges= 75 schur= 1 lambda= 343477585.254023 levenbergIter= 3
iteration= 6 chi2= 5232378.323995 time= 4.0416e-05 cumTime= 0.000385451 edges= 75 schur= 1 lambda= 457970113.672030 levenbergIter= 2
iteration= 7 chi2= 5232378.323995 time= 0.000145913 cumTime= 0.000531364 edges= 75 schur= 1 lambda= 16500112266241431612424192.000000 levenbergIter= 10
optimization costs time: 0.00104973 seconds.
after optimization:
T=
0.997983 0.00518784 0.063265 0.0433475
0.00574846 -0.999946 -0.00868262 0.00580473
0.0632165 0.00902879 -0.997959 0.0564951
0 0 0 1
与左扰动优化的姿态误差 dR=2.82832
与左扰动优化的位置误差 dt=0.172576
与EPNP姿态误差 dR=2.82833
与EPNP位置误差 dt=0.170768
3.2左扰动+左乘更新
修改MyEdgeProjectXYZ2UV::linearizeOplus()函数
void MyEdgeProjectXYZ2UV::linearizeOplus() {
MyVertexSE3Expmap * vj = static_cast<MyVertexSE3Expmap *>(_vertices[1]);
SE3Quat T(vj->estimate());
VertexSBAPointXYZ* vi = static_cast<VertexSBAPointXYZ*>(_vertices[0]);
Vector3D xyz = vi->estimate();
Vector3D xyz_trans = T.map(xyz);
double x = xyz_trans[0];
double y = xyz_trans[1];
double z = xyz_trans[2];
double z_2 = z*z;
const CameraParameters * cam = static_cast<const CameraParameters *>(parameter(0));
Eigen::Matrix<double,2,3,Eigen::ColMajor> tmp;
tmp(0,0) = cam->focal_length;
tmp(0,1) = 0;
tmp(0,2) = -x/z*cam->focal_length;
tmp(1,0) = 0;
tmp(1,1) = cam->focal_length;
tmp(1,2) = -y/z*cam->focal_length;
Eigen::Matrix3d tmp_R = T.rotation().toRotationMatrix();
_jacobianOplusXi = -1./z * tmp * T.rotation().toRotationMatrix();
Eigen::Matrix<double,3,6,Eigen::ColMajor> tmp_p;
// //右扰动
// Eigen::Matrix3d tmp_fx;
// tmp_fx << 0, -xyz[2], xyz[1], xyz[2], 0, -xyz[0], -xyz[1], xyz[0], 0;
// tmp_p.block(0, 0, 3, 3) = -tmp_R * tmp_fx;//对姿态的雅可比 = -R[p]^
// tmp_p.block(0, 3, 3, 3) = Eigen::Matrix3d::Identity(3,3);//对位置的雅可比 = I
//左扰动
xyz = tmp_R * xyz;
Eigen::Matrix3d tmp_fx;
tmp_fx << 0, -xyz[2], xyz[1], xyz[2], 0, -xyz[0], -xyz[1], xyz[0], 0;
tmp_p.block(0, 0, 3, 3) = -tmp_fx;//对姿态的雅可比 = -[Rp]^
tmp_p.block(0, 3, 3, 3) = Eigen::Matrix3d::Identity(3, 3);//对位置的雅可比 = I
Eigen::Matrix<double,2,6,Eigen::ColMajor> jres = (-1./z * tmp * tmp_p);
_jacobianOplusXj = jres;
}
提供EPNP初始值的情况下,输出结果为:
-- Max dist : 94.000000
-- Min dist : 4.000000
一共找到了79组匹配点
3d-2d pairs: 75
R=
[0.9979059095501264, -0.05091940089110115, 0.03988747043654633;
0.0498186625425323, 0.998362315743816, 0.02812094175376019;
-0.04125404886078842, -0.02607491352883862, 0.9988083912027648]
t=
[-0.1267821389558076;
-0.008439496817513407;
0.06034935748888434]
calling bundle adjustment
iteration= 0 chi2= 0.107897 time= 0.000277378 cumTime= 0.000277378 edges= 75 schur= 1 lambda= 71.571421 levenbergIter= 1
iteration= 1 chi2= 0.000010 time= 4.4954e-05 cumTime= 0.000322332 edges= 75 schur= 1 lambda= 23.857140 levenbergIter= 1
iteration= 2 chi2= 0.000000 time= 4.2079e-05 cumTime= 0.000364411 edges= 75 schur= 1 lambda= 15.904760 levenbergIter= 1
iteration= 3 chi2= 0.000000 time= 4.1667e-05 cumTime= 0.000406078 edges= 75 schur= 1 lambda= 10.603173 levenbergIter= 1
iteration= 4 chi2= 0.000000 time= 4.1487e-05 cumTime= 0.000447565 edges= 75 schur= 1 lambda= 7.068782 levenbergIter= 1
iteration= 5 chi2= 0.000000 time= 4.1006e-05 cumTime= 0.000488571 edges= 75 schur= 1 lambda= 4.712522 levenbergIter= 1
iteration= 6 chi2= 0.000000 time= 4.1247e-05 cumTime= 0.000529818 edges= 75 schur= 1 lambda= 3.141681 levenbergIter= 1
iteration= 7 chi2= 0.000000 time= 5.2287e-05 cumTime= 0.000582105 edges= 75 schur= 1 lambda= 2.094454 levenbergIter= 1
iteration= 8 chi2= 0.000000 time= 4.1317e-05 cumTime= 0.000623422 edges= 75 schur= 1 lambda= 1.396303 levenbergIter= 1
iteration= 9 chi2= 0.000000 time= 0.000134671 cumTime= 0.000758093 edges= 75 schur= 1 lambda= 30502.697347 levenbergIter= 6
iteration= 10 chi2= 0.000000 time= 4.1417e-05 cumTime= 0.00079951 edges= 75 schur= 1 lambda= 20335.131565 levenbergIter= 1
iteration= 11 chi2= 0.000000 time= 4.1237e-05 cumTime= 0.000840747 edges= 75 schur= 1 lambda= 13556.754376 levenbergIter= 1
iteration= 12 chi2= 0.000000 time= 4.1197e-05 cumTime= 0.000881944 edges= 75 schur= 1 lambda= 9037.836251 levenbergIter= 1
iteration= 13 chi2= 0.000000 time= 4.2129e-05 cumTime= 0.000924073 edges= 75 schur= 1 lambda= 18075.672502 levenbergIter= 1
optimization costs time: 0.00186419 seconds.
after optimization:
T=
0.997848 -0.0510596 0.0411281 -0.128508
0.0498762 0.998325 0.0293041 -0.0103511
-0.0425555 -0.0271898 0.998724 0.0590491
0 0 0 1
与左扰动优化的姿态误差 dR=6.46337e-05
与左扰动优化的位置误差 dt=5.86872e-05
与EPNP姿态误差 dR=0.00243119
与EPNP位置误差 dt=0.00288491
不提供初始值(初始值为0)的情况下:
-- Max dist : 94.000000
-- Min dist : 4.000000
一共找到了79组匹配点
3d-2d pairs: 75
R=
[0, 0, 0;
0, 0, 0;
0, 0, 0]
t=
[0;
0;
0]
calling bundle adjustment
iteration= 0 chi2= 2491379.880680 time= 0.000318896 cumTime= 0.000318896 edges= 75 schur= 1 lambda= 155.465777 levenbergIter= 1
iteration= 1 chi2= 2350261.880062 time= 0.000102341 cumTime= 0.000421237 edges= 75 schur= 1 lambda= 6633.206464 levenbergIter= 4
iteration= 2 chi2= 2146578.676969 time= 6.0533e-05 cumTime= 0.00048177 edges= 75 schur= 1 lambda= 8844.275286 levenbergIter= 2
iteration= 3 chi2= 309098.883977 time= 5.1737e-05 cumTime= 0.000533507 edges= 75 schur= 1 lambda= 5604.495364 levenbergIter= 1
iteration= 4 chi2= 231829.063429 time= 4.1257e-05 cumTime= 0.000574764 edges= 75 schur= 1 lambda= 3736.330243 levenbergIter= 1
iteration= 5 chi2= 36841.370280 time= 4.1298e-05 cumTime= 0.000616062 edges= 75 schur= 1 lambda= 2490.886828 levenbergIter= 1
iteration= 6 chi2= 9989.648498 time= 4.1357e-05 cumTime= 0.000657419 edges= 75 schur= 1 lambda= 1660.591219 levenbergIter= 1
iteration= 7 chi2= 1690.278853 time= 4.1377e-05 cumTime= 0.000698796 edges= 75 schur= 1 lambda= 1107.060813 levenbergIter= 1
iteration= 8 chi2= 304.200216 time= 4.1277e-05 cumTime= 0.000740073 edges= 75 schur= 1 lambda= 738.040542 levenbergIter= 1
iteration= 9 chi2= 48.131692 time= 4.1157e-05 cumTime= 0.00078123 edges= 75 schur= 1 lambda= 492.027028 levenbergIter= 1
iteration= 10 chi2= 7.356415 time= 4.1237e-05 cumTime= 0.000822467 edges= 75 schur= 1 lambda= 327.359356 levenbergIter= 1
iteration= 11 chi2= 1.071829 time= 4.1247e-05 cumTime= 0.000863714 edges= 75 schur= 1 lambda= 210.999466 levenbergIter= 1
iteration= 12 chi2= 0.151844 time= 4.1067e-05 cumTime= 0.000904781 edges= 75 schur= 1 lambda= 133.853278 levenbergIter= 1
iteration= 13 chi2= 0.021010 time= 4.1317e-05 cumTime= 0.000946098 edges= 75 schur= 1 lambda= 85.541821 levenbergIter= 1
iteration= 14 chi2= 0.002863 time= 4.1207e-05 cumTime= 0.000987305 edges= 75 schur= 1 lambda= 57.027881 levenbergIter= 1
iteration= 15 chi2= 0.000386 time= 4.1247e-05 cumTime= 0.00102855 edges= 75 schur= 1 lambda= 38.018587 levenbergIter= 1
iteration= 16 chi2= 0.000052 time= 4.1147e-05 cumTime= 0.0010697 edges= 75 schur= 1 lambda= 25.345725 levenbergIter= 1
iteration= 17 chi2= 0.000007 time= 4.0876e-05 cumTime= 0.00111058 edges= 75 schur= 1 lambda= 16.897150 levenbergIter= 1
iteration= 18 chi2= 0.000001 time= 4.1156e-05 cumTime= 0.00115173 edges= 75 schur= 1 lambda= 11.264767 levenbergIter= 1
iteration= 19 chi2= 0.000000 time= 4.1116e-05 cumTime= 0.00119285 edges= 75 schur= 1 lambda= 7.509844 levenbergIter= 1
iteration= 20 chi2= 0.000000 time= 4.2449e-05 cumTime= 0.0012353 edges= 75 schur= 1 lambda= 5.006563 levenbergIter= 1
iteration= 21 chi2= 0.000000 time= 4.1377e-05 cumTime= 0.00127667 edges= 75 schur= 1 lambda= 3.337709 levenbergIter= 1
iteration= 22 chi2= 0.000000 time= 4.1327e-05 cumTime= 0.001318 edges= 75 schur= 1 lambda= 2.225139 levenbergIter= 1
iteration= 23 chi2= 0.000000 time= 4.0997e-05 cumTime= 0.001359 edges= 75 schur= 1 lambda= 1.483426 levenbergIter= 1
iteration= 24 chi2= 0.000000 time= 4.1067e-05 cumTime= 0.00140006 edges= 75 schur= 1 lambda= 0.988951 levenbergIter= 1
iteration= 25 chi2= 0.000000 time= 4.1147e-05 cumTime= 0.00144121 edges= 75 schur= 1 lambda= 0.659300 levenbergIter= 1
iteration= 26 chi2= 0.000000 time= 4.1097e-05 cumTime= 0.00148231 edges= 75 schur= 1 lambda= 0.439534 levenbergIter= 1
iteration= 27 chi2= 0.000000 time= 4.1067e-05 cumTime= 0.00152337 edges= 75 schur= 1 lambda= 0.293022 levenbergIter= 1
iteration= 28 chi2= 0.000000 time= 4.1017e-05 cumTime= 0.00156439 edges= 75 schur= 1 lambda= 0.195348 levenbergIter= 1
iteration= 29 chi2= 0.000000 time= 4.1027e-05 cumTime= 0.00160542 edges= 75 schur= 1 lambda= 0.130232 levenbergIter= 1
iteration= 30 chi2= 0.000000 time= 4.1277e-05 cumTime= 0.0016467 edges= 75 schur= 1 lambda= 0.086821 levenbergIter= 1
iteration= 31 chi2= 0.000000 time= 5.1576e-05 cumTime= 0.00169827 edges= 75 schur= 1 lambda= 0.057881 levenbergIter= 1
iteration= 32 chi2= 0.000000 time= 4.1057e-05 cumTime= 0.00173933 edges= 75 schur= 1 lambda= 0.038587 levenbergIter= 1
iteration= 33 chi2= 0.000000 time= 4.0807e-05 cumTime= 0.00178014 edges= 75 schur= 1 lambda= 0.025725 levenbergIter= 1
iteration= 34 chi2= 0.000000 time= 4.0576e-05 cumTime= 0.00182071 edges= 75 schur= 1 lambda= 0.017150 levenbergIter= 1
iteration= 35 chi2= 0.000000 time= 4.1187e-05 cumTime= 0.0018619 edges= 75 schur= 1 lambda= 0.011433 levenbergIter= 1
iteration= 36 chi2= 0.000000 time= 4.1057e-05 cumTime= 0.00190296 edges= 75 schur= 1 lambda= 0.007622 levenbergIter= 1
iteration= 37 chi2= 0.000000 time= 4.1007e-05 cumTime= 0.00194396 edges= 75 schur= 1 lambda= 0.005081 levenbergIter= 1
iteration= 38 chi2= 0.000000 time= 4.1016e-05 cumTime= 0.00198498 edges= 75 schur= 1 lambda= 0.003388 levenbergIter= 1
iteration= 39 chi2= 0.000000 time= 4.0976e-05 cumTime= 0.00202595 edges= 75 schur= 1 lambda= 0.002258 levenbergIter= 1
iteration= 40 chi2= 0.000000 time= 4.0766e-05 cumTime= 0.00206672 edges= 75 schur= 1 lambda= 0.001506 levenbergIter= 1
iteration= 41 chi2= 0.000000 time= 4.0967e-05 cumTime= 0.00210769 edges= 75 schur= 1 lambda= 0.001004 levenbergIter= 1
iteration= 42 chi2= 0.000000 time= 4.1237e-05 cumTime= 0.00214892 edges= 75 schur= 1 lambda= 0.000669 levenbergIter= 1
iteration= 43 chi2= 0.000000 time= 4.0646e-05 cumTime= 0.00218957 edges= 75 schur= 1 lambda= 0.000446 levenbergIter= 1
iteration= 44 chi2= 0.000000 time= 4.0626e-05 cumTime= 0.0022302 edges= 75 schur= 1 lambda= 0.000297 levenbergIter= 1
iteration= 45 chi2= 0.000000 time= 0.000169557 cumTime= 0.00239975 edges= 75 schur= 1 lambda= 53222.844307 levenbergIter= 8
iteration= 46 chi2= 0.000000 time= 4.0826e-05 cumTime= 0.00244058 edges= 75 schur= 1 lambda= 35481.896205 levenbergIter= 1
iteration= 47 chi2= 0.000000 time= 4.1106e-05 cumTime= 0.00248169 edges= 75 schur= 1 lambda= 23654.597470 levenbergIter= 1
iteration= 48 chi2= 0.000000 time= 4.0676e-05 cumTime= 0.00252236 edges= 75 schur= 1 lambda= 15769.731647 levenbergIter= 1
iteration= 49 chi2= 0.000000 time= 5.9401e-05 cumTime= 0.00258176 edges= 75 schur= 1 lambda= 21026.308862 levenbergIter= 2
iteration= 50 chi2= 0.000000 time= 4.0987e-05 cumTime= 0.00262275 edges= 75 schur= 1 lambda= 14017.539241 levenbergIter= 1
iteration= 51 chi2= 0.000000 time= 4.4683e-05 cumTime= 0.00266743 edges= 75 schur= 1 lambda= 28035.078483 levenbergIter= 1
optimization costs time: 0.00590244 seconds.
after optimization:
T=
0.936247 0.0629721 -0.345653 0.974379
0.175357 -0.936262 0.304407 -0.498621
-0.304452 -0.345613 -0.887615 -2.23452
0 0 0 1
与左扰动优化的姿态误差 dR=2.78006
与左扰动优化的位置误差 dt=2.59136
与EPNP姿态误差 dR=2.78033
与EPNP位置误差 dt=2.59216