学习笔记三：深度学习DNN2

一、神经网络参数优化器

参考曹健《人工智能实践：Tensorflow2.0 》
深度学习优化算法经历了SGD -> SGDM -> NAG ->AdaGrad -> AdaDelta -> Adam -> Nadam
这样的发展历程。

• 上图中f一般指loss
• 一阶动量：与梯度相关的函数
• 二阶动量：与梯度平方相关的函数
• 不同的优化器，实质上只是定义了不同的一阶动量和二阶动量公式

1.2 SGD（无动量）随机梯度下降。

• 最常用的梯度下降方法是随机梯度下降，即随机采集样本来计算梯度。根据统计学知识有：采样数据的平均值为全量数据平均值的无偏估计。
• 实际计算出来的SGD在全量梯度附近以一定概率出现，batch_size越大，概率分布的方差越小，SGD梯度就越确定，相当于在全量梯度上注入了噪声。适当的噪声是有益的。
• batch_size越小，计算越快，w更新越频繁，学习越快。但是太小的话，SGD梯度和真实梯度差异过大，而且震荡厉害，不利于学习
• SGD梯度有一定随机性，所以可以逃离鞍点、平坦极小值或尖锐极小值区域
• 最初版本是vanilla SGD，没有动量。$m_t=g_t，V_t=1$（p32—sgd.py）

• 每个bacth_size样本的梯度都不一样，甚至前后差异很大，造成梯度震荡。（比如一个很大的正值接一个很大的负值）

• 神经网络中，输入归一化。但是多层非线性变化后，中间层输入各维度数值差别可能很大。不同方向的敏感度不一样。有的方向更陡，容易震荡。

• vanilla SGD最大的缺点是下降速度慢，而且可能会在沟壑的两边持续震荡，停留在一个局部最优
  点

# sgd
w1.assign_sub(learning_rate * grads[0])
b1.assign_sub(learning_rate * grads[1])

1.3 SGDM——引入动量减少震荡

• 动量法是一种使梯度向量向相关方向加速变化，抑制震荡，最终实现加速收敛的方法。

• 为了抑制SGD的震荡，SGDM认为 梯度下降过程可以加入惯性。如果前后梯度方向相反，动量对冲，减少震荡。如果前后方向相同，步伐加大，加快学习速度。

• SGDM全称是SGD with Momentum，在SGD基础上引入了一阶动量：
  

• 一阶动量是各个时刻梯度方向的指数移动平均值，约等于最近$1/(1-{\beta }_1)$个时刻的梯度向量和的平均值。(指数移动平均值大约是过去一段时间的平均值，反映“局部的”参数信息$)。{\beta }_1$的经验值为0.9。所以t 时刻的下降方向主要偏向此前累积的下降方向，并略微偏向当前时刻的下降方向。
  
  老师书上写$$W_{t+1}=W_t-v_t=W_t-(\alpha v_{t-1}+\epsilon g_t)$$
  $\alpha 、\epsilon$是超参数。

• SGDM问题1：时刻t的主要下降方向是由累积动量决定的，自己的梯度方向说了也不算。

• SGD/SGDM 问题2:会被困在一个局部最优点里

• SGDM 问题3：如果梯度连续多次迭代都是一个方向，剃度一直增大，最后造成梯度爆炸

# sgd-momentun
beta = 0.9
m_w = beta * m_w + (1 - beta) * grads[0]
m_b = beta * m_b + (1 - beta) * grads[1]
w1.assign_sub(learning_rate * m_w)
b1.assign_sub(learning_rate * m_b)

1.4 SGD with Nesterov Acceleration

• SGDM：主要看当前梯度方向。计算当前loss对w梯度，再根据历史梯度计算一阶动量$m_t$
• NAG：主要看动量累积之后的梯度方向。 计算参数在累积动量之后的更新值，并计算此时梯度，再将这个梯度带入计算一阶动量$m_t$
• 主要差别在于是否先对w减去累积动量
  
  思路如下图：

首先，按照原来的更新方向更新一步（棕色线），然后计算该新位置的梯度方向（红色线），然后
用这个梯度方向修正最终的更新方向（绿色线）。上图中描述了两步的更新示意图，其中蓝色线是标准momentum更新路径。

1.5 AdaGrad——累积全部梯度，自适应学习率

• SGD:对所有的参数使用统一的、固定的学习率
• AdaGrad:自适应学习率。对于频繁更新的参数，不希望被单个样本影响太大，我们给它们很小的学习率；对于偶尔出现的参数，希望能多得到一些信息，我们给它较大的学习率。
• 另一个解释是：初始时刻W离最优点远，学习率需要设置的大一些。随着学习你的进行，离最优点越近，学习率需要不断减小。
• 引入二阶动量——该维度上，所有梯度值的平方和(梯度按位相乘后求和），来度量参数更新频率，用以对学习率进行缩放。（频繁更新的参数、越到学习后期参数也被更新的越多，二阶动量都越大，学习率越小）
  $$V_t=\sum _{\tau =1}^t{g}_{\tau }^2$$
  $${\eta }_t=lr\cdot m_t/\sqrt{V_t}=lr\cdot g_t/\sqrt{\sum _{\tau =1}^t{g}_{\tau }^2}$$
  $$W_{t+1}=W_t-{\eta }_t$$
  
• 优点：AdaGrad 在稀疏数据场景下表现最好。因为对于频繁出现的参数，学习率衰减得快；对于稀疏的参数，学习率衰减得更慢。
• 缺点：在实际很多情况下，频繁更新的参数，学习率会很快减至 0 ，导致参数不再更新，训练过程提前结束。（二阶动量呈单调递增，累计从训练开始的梯度)

# adagrad
v_w += tf.square(grads[0])
v_b += tf.square(grads[1])
w1.assign_sub(learning_rate * grads[0] / tf.sqrt(v_w))
b1.assign_sub(learning_rate * grads[1] / tf.sqrt(v_b))

1.6 RMSProp——累积最近时刻梯度

• RMSProp算法的全称叫 Root Mean Square Prop。AdaGrad 的学习率衰减太过激进，考虑改变二阶动量的计算策略：不累计全部梯度，只关注过去某一窗口内的梯度。
• 指数移动平均值大约是过去一段时间的平均值，反映“局部的”参数信息，因此我们用这个方法来计算二阶累积动量：（分母会再加一个平滑项，防止为0）
  
  对照SGDM的一阶动量公式：
  

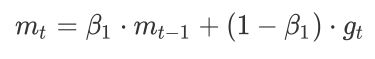
# RMSProp
beta = 0.9
v_w = beta * v_w + (1 - beta) * tf.square(grads[0])
v_b = beta * v_b + (1 - beta) * tf.square(grads[1])
w1.assign_sub(learning_rate * grads[0] / tf.sqrt(v_w))
b1.assign_sub(learning_rate * grads[1] / tf.sqrt(v_b))

1.7 Adam

将SGDM一阶动量和RMSProp二阶动量结合起来，再修正偏差，就是Adam。

一阶动量和二阶动量都是按照指数移动平均值进行计算的。初始化 $m_0=0,V_0=0$，在初期，迭
代得到的$m_t、V_t$会接近于0。我们可以通过偏差修正来解决这一问题：
$$m_t=\frac{m_t}{1-{\beta }_1^t}$$
$$V_t=\frac{V_t}{1-{\beta }_2^t}$$
$${\eta }_t=lr\cdot m_t/(\sqrt{V_t}+\epsilon )$$
$$W_{t+1}=W_t-{\eta }_t$$

• $1-{\beta }_1^t、1-{\beta }_2^t$的取值范围为（0,1）,可以将开始阶段$m_t、V_t$放大至$m_t、V_t$。
• 随着迭代次数t的增加，${\beta }_1^t、{\beta }_2^t$趋近于0，放大倍数趋近于1，即不再放大$m_t、V_t$。

# adam
m_w = beta1 * m_w + (1 - beta1) * grads[0]
m_b = beta1 * m_b + (1 - beta1) * grads[1]
v_w = beta2 * v_w + (1 - beta2) * tf.square(grads[0])
v_b = beta2 * v_b + (1 - beta2) * tf.square(grads[1])
m_w_correction = m_w / (1 - tf.pow(beta1, int(global_step)))
m_b_correction = m_b / (1 - tf.pow(beta1, int(global_step)))
v_w_correction = v_w / (1 - tf.pow(beta2, int(global_step)))
v_b_correction = v_b / (1 - tf.pow(beta2, int(global_step)))
w1.assign_sub(learning_rate * m_w_correction / tf.sqrt(v_w_correction))
b1.assign_sub(learning_rate * m_b_correction / tf.sqrt(v_b_correction))

1.8 悬崖、鞍点问题

• 高维空间中，一个点各个方向导数为0，只要有一个方向对应的极值和其它方向不一样，该点就是鞍点。鞍点是一个不稳定的点，梯度轻微扰动就可以逃离。
• SGD梯度因为具有一定的随机性，反而可以逃离鞍点
• 例如n维空间中，某点各方向导数都为0。假设其中极大或者极小的概率为0.5，则该点为极大或极小值概率均为$0.5^n$，反之为鞍点的概率为$1-2\ast 0.5^n=1-0.5^{n-1}$。高维空间中鞍点概率几乎为1。因此不必非要找到极小值，只需要loss降到比较低就行了。
• 梯度裁剪：悬崖部位loss会突然下降，梯度太大W容易走过头，所以可以梯度裁剪，限制梯度最大值。

二、过拟合解决方案

2.1 正则化

• 逻辑回归中，损失函数为$Loss+\lambda \left|W\right|orLoss+\lambda \Vert W\Vert$。在神经网络中则更加灵活。可以为不同层分别设置L1或者L2正则，且系数$\lambda$也可以不同。即各层正则化项可以完全独立。
• L1正则可以对神经网络剪枝（很多权重趋近于0），网络运行速度可以大大加快。所以对实时要求高的场景可以用L1正则。
• 神经网络中可以设置前层的正则化项系数$\lambda$更大，后层小一些。因为前层面对真实物理信号，噪声较大。为了过滤噪声，W应当较小，$\lambda$更大。且后层面对输出，正则化太厉害，影响分类效果。

2.2 dropout

1. Dropout：每次训练时直接随机去除部分神经元。可以达到剪枝的目的，生成新的子网络。所以本质也是一种正则化，类比于L1正则。各层可以独立设置Dropout
2. dropout相当于训练大量子网络，预测时使用全部神经元，等同于集成学习，增加泛化能力。
3. 降低模型复杂度和各神经元之间的依赖程度，降低模型对某一特征的过度依赖，从而降低过拟合

• 子网络可以是海量的，大量子网络可能没有训练或者就训练一次，但是由于大部分神经元是一样的，少部分才被去除，所以大部分自网络高度相关。而且训练一个子网络，等于主网络大部分参数也得到了更新
• dropout是随机去除神经元，所以发生在$d^k=W^k\cdot a^{k-1}$加权求和的时候，而不是$a^{k-1}=f(d^{l-1}+w_0^{k-1})$激活之后。
• 训练时dropout概率为p，即只有（1-p)个神经元进行计算。则预测时结果要乘以（1-p）
• 跟正则化系数一样，dropout应该是前层设置的高。前层噪声多，需要过滤。后层主要用来精确拟合，dropout过高，影响预测结果。
• dropout可以取代正则，例如训练100个神经元，dropout=0.2；效果好于训练80个神经元。

2.3 Batch Normalization

神经网络学习隐含条件：输入数据有一定的规律，符合一定的概率分布，模型就是学习输入分布和类别之间的映射关系。但是神经网络中，各层输入分布并不稳定：

1. SGD训练时，随机选取样本，造成分布的差异，即$\mu /\sigma$都不一样
2. 前层权重W的变化造成后层输入的变化，进而导致后层最优的参数W变化。即使后层参数已接近最优，也要重新学习，造成网络不稳定。后层分布累积了前层所有的W，所以不同轮次输入分布差异很大，学习速度会很慢

即训练样本数据本身是符合一定的概率分布的，但是因为以上两个原因，造成每个batch训练时概率分布差异很大。

对于一个batch的数据，第l层第m个神经元来说：

• 计算神经元在一个batch样本的输入$d_{i,m}^l$的均值和方差，将数据分布转为标准正态分布
  $${\mu }_m^l=\frac{1}{batch-size}\sum _{iϵbatch}{d}_{i,m}^l$$
• 通过两个待学习参数${\beta }_1,{\gamma }_1$，将标准正态分布调整至$N({\beta }_1,{\gamma }_1)$。

BN的作用：

• 使输入数据对应的概率分布保持不变（不是数值不变）。无论训练集数据如何选择，前层网络参数如何变化，各层接受的输入分布在不同的训练阶段都是一致的，各层最优参数稳定，提高了收敛速度
• 不容易受极端数据影响，所以可以提高学习率，使收敛速度进一步提高。
• 降低对参数初始化的依赖程度
• 对参数进行正则化，提高了模型泛化能力

其它注意点：

• batch_size不宜过低，否则均值方差估计不准
• 预测时没有批量的概念，都是对单个样本进行预测，无法进行BN操作计算$\mu /\sigma$ 。所以要保存训练中计算的$\mu /\sigma$ ，预测时使用它们进行无偏估计（公式中t表示当前迭代次数，T为总迭代次数)
  $$\mu =\frac{1}{T}\sum _{t=1}^T{\mu }_t$$
  $$\sigma =\sqrt{\frac{1}{T-1}\sum _{t=1}^T{\sigma }_t^2}$$
• BN的位置在激活函数之前。因为将输入转换为正态分布$N({\beta }_1,{\gamma }_1)$的前提是输入数据本身符合正态分布。而神经网络中激活函数的值域往往有限，造成激活后的输出不会符合正态分布。这样BN之后也不会符合正态分布。

2.4 Layer Normalization

• Batch Normalization：在某一个神经元，所有batch个样本上进行归一化，即归一化不同样本的同一特征
• Layer Normalization：对某一个样本，同一层全部神经元上进行归一化，即归一化一个样本所有特征
• BN和LN都可以用的时候BN一般更好，因为不同数据，同一特征得到的归一化结果更不容易造成信息损失。LN会造成神经元耦合。
• batch_size过小的场合，或者RNN、LSTM、Attention等变长神经网络一般使用LN。（变长神经网络虽然填充到同一长度，但是pad部分是没有意义的，进行特征维度归一化也没用实际意义。NLP任务中一个序列的所有token都是同一语义空间，进行LN归一化有实际意义）

对于l层第i个样本有：（l层共有m=1、2、…$M^l$个神经元）
$${\mu }_i^l=\frac{1}{M^l}\sum _{m=1}^{M^l}{d}_{i,m}^l$$
计算出$\mu /\sigma$后，和BN一样将数据归一化为$N({\beta }_1,{\gamma }_1)$分布。

综合之前的讲解：
model.train()的作用是启用 Batch Normalization 和 Dropout。model.eval()的作用是不启用 Batch Normalization 和 Dropout。