深入浅出Pytorch中的计算细节_input/output
准备工作
- 导入依赖
- 准备data_iter
- 查看input/output shape
import torch
from torch import nn
from d2l import torch as d2l
# 2. 准备data_iter
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
obx,oby = next(iter(train_iter))
# 3. 查看input/output shape
obx.shape # torch.Size([256, 1, 28, 28])
obx[1][0].shape # torch.Size([28,28])
oby[1] # 9
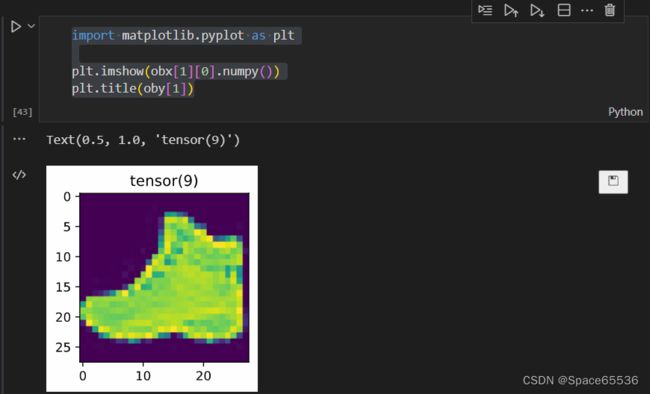
可视化
import matplotlib.pyplot as plt
plt.imshow(obx[1][0].numpy())
plt.title(oby[1])
不同模型
torch.nn.Flatten()
m = nn.Flatten()
output = m(obx)
output.shape # torch.Size([256, 784])
torch.nn.Linear()
m1 = nn.Linear(28,10) #
m2 = nn.Sequential(nn.Flatten(),nn.Linear(784,10))
# obx的[256, 1, 28, 28]与m1的[28,10]
output1 = m1(obx)
# obx的[256, 1, 28, 28]→Flatten→[256,784]→Linear的[784,10]
output2 = m2(obx)
output1.shape # torch.Size([256, 1, 28, 10])
output2.shape # torch.Size([256, 10])
例2:
input_linear = torch.randn([128,64,16,8])
m_linear = nn.Linear(8,3)
output_linear = m_linear(input_linear)
output_linear.shape # torch.Size([128, 64, 16, 3])
- nn.Linear(input,output) 中input需和x的output同(或者结合矩阵乘法来思考)
torch.nn.Conv2d()
参考:CNN卷积层的计算细节
# torch.randn([minibatch,out_channels,heigth,width])
input_conv2d = torch.randn([256,3,227,227])
# nn.Conv2d(in_channels,out_channels,kernel_size,stride,
# padding,dilation,groups,bias,padding_mode,device,dtype)
m_conv2d = nn.Conv2d(3,3,kernel_size=(11,11))
# in_channels = 8,out_channels = 3
output_conv2d = m_conv2d(input_conv2d)
# output_conv2d(minibatch,out_channels,heigth,width)
output_conv2d.shape # torch.Size([128, 3, 14, 6])
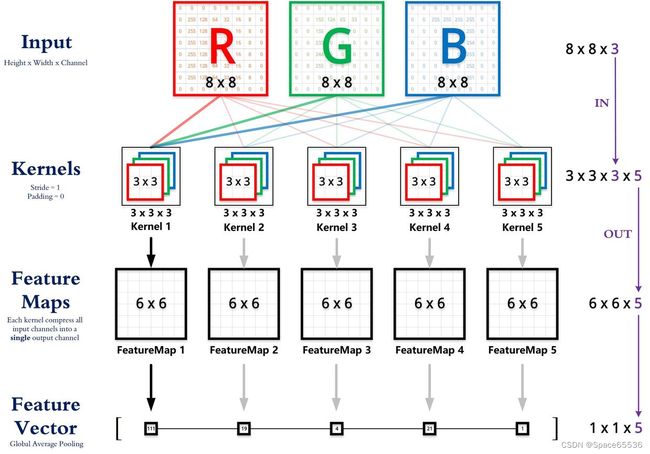
输入矩阵、权重矩阵、输出矩阵这三者之间的相互决定关系
卷积核的输入通道数(in depth)由输入矩阵的通道数所决定。(红色标注)
输出矩阵的通道数(out depth)由卷积核的输出通道数所决定。(绿色标注)
输出矩阵的高度和宽度(height, width)这两个维度的尺寸由输入矩阵、卷积核、扫描方式所共同决定。计算公式如下。(蓝色标注)
再理解Conv2d
再从一个Error来理解卷积层进行卷积操作中参数的变化过程:
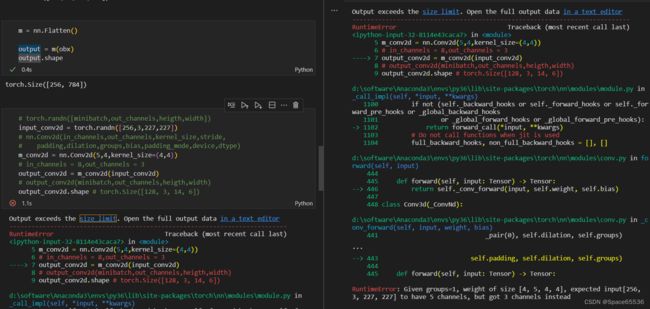
报错提示:
RuntimeError: Given groups=1, weight of size [4, 5, 4, 4], expected input[256, 3, 227, 227] to have 5 channels, but got 3 channels instead
要搞清报错的原因,参考上面,我们可以从2个角度来考虑
- 输入卷积层的东西:images集合的shape(batchsize,channels,height,width)
- 卷积层Conv2d的东西:它自己的shape,input/output_features,input/output_channels,kernel相关参数(shape))
首先是输入卷积层的东西,Conv2d(in_channels,out_channels,kernel_size,**args)
-
根据“卷积核的输入通道数(in depth)由输入矩阵的通道数所决定”,所以,Conv2d的in_channels(为什么这个参数,见下面对应的源码)应该为输入矩阵的通道数,也就是前面的3;
-
根据“输出矩阵的通道数(out depth)由卷积核的输出通道数所决定“,所以,Conv2d的out_channels(为什么这个参数,见下面对应的源码对应了后面output_conv2d.shape(batchsize,out_depth,out_height,out_width);

-
根据“输出矩阵的高度和宽度这两个维度尺寸由输入矩阵,卷积核,扫描方式(kernel_size,stride,padding)共同决定”,所以,再根据两个公式,我们可以算出out_height,out_width:
-
h e i g h t o u t = ( h e i g h t i n − h e i g h t k e r n e l + 2 ∗ p a d d i n g ) / s t r i d e + 1 height_{out} = (height_{in} - height_{kernel}+2*padding)/stride + 1 heightout=(heightin−heightkernel+2∗padding)/stride+1
- 13 = (16-4)/1 + 1
-
w i d t h o u t = ( w i d t h i n − w i d t h k e r n e l + 2 ∗ p a d d i n g ) / s t r i d e + 1 width_{out} = (width_{in} - width_{kernel}+2*padding)/stride + 1 widthout=(widthin−widthkernel+2∗padding)/stride+1
- 5 = (8 - 4)/1 + 1
原理
矩阵乘法与广播机制
示例
Notes: A m ∗ n × B n ∗ p A_{m*n} \times B_{n*p} Am∗n×Bn∗p 这两个矩阵的中间维度 n 需要相同
相关模型的源码及部分解释
torch.nn.FLatten()
class Flatten(Module):
r"""
Flattens a contiguous range of dims into a tensor. For use with :class:`~nn.Sequential`.
Shape:
- Input: :math:`(*, S_{\text{start}},..., S_{i}, ..., S_{\text{end}}, *)`,'
where :math:`S_{i}` is the size at dimension :math:`i` and :math:`*` means any
number of dimensions including none.
- Output: :math:`(*, \prod_{i=\text{start}}^{\text{end}} S_{i}, *)`.
Args:
start_dim: first dim to flatten (default = 1).
end_dim: last dim to flatten (default = -1).
Examples::
>>> input = torch.randn(32, 1, 5, 5)
>>> m = nn.Sequential(
>>> nn.Conv2d(1, 32, 5, 1, 1),
>>> nn.Flatten()
>>> )
>>> output = m(input)
>>> output.size()
torch.Size([32, 288])
"""
__constants__ = ['start_dim', 'end_dim']
start_dim: int
end_dim: int
def __init__(self, start_dim: int = 1, end_dim: int = -1) -> None:
super(Flatten, self).__init__()
self.start_dim = start_dim
self.end_dim = end_dim
def forward(self, input: Tensor) -> Tensor:
return input.flatten(self.start_dim, self.end_dim)
def extra_repr(self) -> str:
return 'start_dim={}, end_dim={}'.format(
self.start_dim, self.end_dim
)
torch.nn.Linear()
class Linear(Module):
r"""Applies a linear transformation to the incoming data: :math:`y = xA^T + b`
This module supports :ref:`TensorFloat32`.
Args:
in_features: size of each input sample
out_features: size of each output sample
bias: If set to ``False``, the layer will not learn an additive bias.
Default: ``True``
Shape:
- Input: :math:`(*, H_{in})` where :math:`*` means any number of
dimensions including none and :math:`H_{in} = \text{in\_features}`.
- Output: :math:`(*, H_{out})` where all but the last dimension
are the same shape as the input and :math:`H_{out} = \text{out\_features}`.
Attributes:
weight: the learnable weights of the module of shape
:math:`(\text{out\_features}, \text{in\_features})`. The values are
initialized from :math:`\mathcal{U}(-\sqrt{k}, \sqrt{k})`, where
:math:`k = \frac{1}{\text{in\_features}}`
bias: the learnable bias of the module of shape :math:`(\text{out\_features})`.
If :attr:`bias` is ``True``, the values are initialized from
:math:`\mathcal{U}(-\sqrt{k}, \sqrt{k})` where
:math:`k = \frac{1}{\text{in\_features}}`
Examples::
>>> m = nn.Linear(20, 30)
>>> input = torch.randn(128, 20)
>>> output = m(input)
>>> print(output.size())
torch.Size([128, 30])
"""
__constants__ = ['in_features', 'out_features']
in_features: int
out_features: int
weight: Tensor
def __init__(self, in_features: int, out_features: int, bias: bool = True,
device=None, dtype=None) -> None:
factory_kwargs = {'device': device, 'dtype': dtype}
super(Linear, self).__init__()
self.in_features = in_features
self.out_features = out_features
self.weight = Parameter(torch.empty((out_features, in_features), **factory_kwargs))
if bias:
self.bias = Parameter(torch.empty(out_features, **factory_kwargs))
else:
self.register_parameter('bias', None)
self.reset_parameters()
def reset_parameters(self) -> None:
# Setting a=sqrt(5) in kaiming_uniform is the same as initializing with
# uniform(-1/sqrt(in_features), 1/sqrt(in_features)). For details, see
# https://github.com/pytorch/pytorch/issues/57109
init.kaiming_uniform_(self.weight, a=math.sqrt(5))
if self.bias is not None:
fan_in, _ = init._calculate_fan_in_and_fan_out(self.weight)
bound = 1 / math.sqrt(fan_in) if fan_in > 0 else 0
init.uniform_(self.bias, -bound, bound)
def forward(self, input: Tensor) -> Tensor:
return F.linear(input, self.weight, self.bias)
def extra_repr(self) -> str:
return 'in_features={}, out_features={}, bias={}'.format(
self.in_features, self.out_features, self.bias is not None
)
torch.nn.conv2d()
class Conv2d(_ConvNd):
__doc__ = r"""Applies a 2D convolution over an input signal composed of several input
planes.
In the simplest case, the output value of the layer with input size
:math:`(N, C_{\text{in}}, H, W)` and output :math:`(N, C_{\text{out}}, H_{\text{out}}, W_{\text{out}})`
can be precisely described as:
.. math::
\text{out}(N_i, C_{\text{out}_j}) = \text{bias}(C_{\text{out}_j}) +
\sum_{k = 0}^{C_{\text{in}} - 1} \text{weight}(C_{\text{out}_j}, k) \star \text{input}(N_i, k)
where :math:`\star` is the valid 2D `cross-correlation`_ operator,
:math:`N` is a batch size, :math:`C` denotes a number of channels,
:math:`H` is a height of input planes in pixels, and :math:`W` is
width in pixels.
""" + r"""
This module supports :ref:`TensorFloat32`.
* :attr:`stride` controls the stride for the cross-correlation, a single
number or a tuple.
* :attr:`padding` controls the amount of padding applied to the input. It
can be either a string {{'valid', 'same'}} or a tuple of ints giving the
amount of implicit padding applied on both sides.
* :attr:`dilation` controls the spacing between the kernel points; also
known as the à trous algorithm. It is harder to describe, but this `link`_
has a nice visualization of what :attr:`dilation` does.
{groups_note}
The parameters :attr:`kernel_size`, :attr:`stride`, :attr:`padding`, :attr:`dilation` can either be:
- a single ``int`` -- in which case the same value is used for the height and width dimension
- a ``tuple`` of two ints -- in which case, the first `int` is used for the height dimension,
and the second `int` for the width dimension
Note:
{depthwise_separable_note}
Note:
{cudnn_reproducibility_note}
Note:
``padding='valid'`` is the same as no padding. ``padding='same'`` pads
the input so the output has the shape as the input. However, this mode
doesn't support any stride values other than 1.
Args:
in_channels (int): Number of channels in the input image
out_channels (int): Number of channels produced by the convolution
kernel_size (int or tuple): Size of the convolving kernel
stride (int or tuple, optional): Stride of the convolution. Default: 1
padding (int, tuple or str, optional): Padding added to all four sides of
the input. Default: 0
padding_mode (string, optional): ``'zeros'``, ``'reflect'``,
``'replicate'`` or ``'circular'``. Default: ``'zeros'``
dilation (int or tuple, optional): Spacing between kernel elements. Default: 1
groups (int, optional): Number of blocked connections from input
channels to output channels. Default: 1
bias (bool, optional): If ``True``, adds a learnable bias to the
output. Default: ``True``
""" .format(**reproducibility_notes, **convolution_notes) + r"""
Shape:
- Input: :math:`(N, C_{in}, H_{in}, W_{in})`
- Output: :math:`(N, C_{out}, H_{out}, W_{out})` where
.. math::
H_{out} = \left\lfloor\frac{H_{in} + 2 \times \text{padding}[0] - \text{dilation}[0]
\times (\text{kernel\_size}[0] - 1) - 1}{\text{stride}[0]} + 1\right\rfloor
.. math::
W_{out} = \left\lfloor\frac{W_{in} + 2 \times \text{padding}[1] - \text{dilation}[1]
\times (\text{kernel\_size}[1] - 1) - 1}{\text{stride}[1]} + 1\right\rfloor
Attributes:
weight (Tensor): the learnable weights of the module of shape
:math:`(\text{out\_channels}, \frac{\text{in\_channels}}{\text{groups}},`
:math:`\text{kernel\_size[0]}, \text{kernel\_size[1]})`.
The values of these weights are sampled from
:math:`\mathcal{U}(-\sqrt{k}, \sqrt{k})` where
:math:`k = \frac{groups}{C_\text{in} * \prod_{i=0}^{1}\text{kernel\_size}[i]}`
bias (Tensor): the learnable bias of the module of shape
(out_channels). If :attr:`bias` is ``True``,
then the values of these weights are
sampled from :math:`\mathcal{U}(-\sqrt{k}, \sqrt{k})` where
:math:`k = \frac{groups}{C_\text{in} * \prod_{i=0}^{1}\text{kernel\_size}[i]}`
Examples:
>>> # With square kernels and equal stride
>>> m = nn.Conv2d(16, 33, 3, stride=2)
>>> # non-square kernels and unequal stride and with padding
>>> m = nn.Conv2d(16, 33, (3, 5), stride=(2, 1), padding=(4, 2))
>>> # non-square kernels and unequal stride and with padding and dilation
>>> m = nn.Conv2d(16, 33, (3, 5), stride=(2, 1), padding=(4, 2), dilation=(3, 1))
>>> input = torch.randn(20, 16, 50, 100)
>>> output = m(input)
.. _cross-correlation:
https://en.wikipedia.org/wiki/Cross-correlation
.. _link:
https://github.com/vdumoulin/conv_arithmetic/blob/master/README.md
"""
def __init__(
self,
in_channels: int,
out_channels: int,
kernel_size: _size_2_t,
stride: _size_2_t = 1,
padding: Union[str, _size_2_t] = 0,
dilation: _size_2_t = 1,
groups: int = 1,
bias: bool = True,
padding_mode: str = 'zeros', # TODO: refine this type
device=None,
dtype=None
) -> None:
factory_kwargs = {'device': device, 'dtype': dtype}
kernel_size_ = _pair(kernel_size)
stride_ = _pair(stride)
padding_ = padding if isinstance(padding, str) else _pair(padding)
dilation_ = _pair(dilation)
super(Conv2d, self).__init__(
in_channels, out_channels, kernel_size_, stride_, padding_, dilation_,
False, _pair(0), groups, bias, padding_mode, **factory_kwargs)
def _conv_forward(self, input: Tensor, weight: Tensor, bias: Optional[Tensor]):
if self.padding_mode != 'zeros':
return F.conv2d(F.pad(input, self._reversed_padding_repeated_twice, mode=self.padding_mode),
weight, bias, self.stride,
_pair(0), self.dilation, self.groups)
return F.conv2d(input, weight, bias, self.stride,
self.padding, self.dilation, self.groups)
def forward(self, input: Tensor) -> Tensor:
return self._conv_forward(input, self.weight, self.bias)