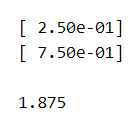python---cvxopt.solvers.qp(P,q,G,h,A,b)
标准形式:
m i n 1 2 x T P x + q T x s . t . G x ≤ h A x = b min\,\,\frac{1}{2}x^TPx+q^Tx\\ s.t.\,\,Gx≤h\\ Ax=b min21xTPx+qTxs.t.Gx≤hAx=b
注意: P P P为对称矩阵, x x x是列向量。
示例:
1 2 [ x 1 x 2 ] [ a b b d ] [ x 1 x 2 ] = 1 2 ( a x 1 2 + d x 2 2 + 2 b x 1 x 2 ) \frac{1}{2}\begin{bmatrix}x_1&x_2\end{bmatrix} \begin{bmatrix}a&b\\b&d\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}= \frac{1}{2}\left(ax_1^2+dx_2^2+2bx_1x_2\right) 21[x1x2][abbd][x1x2]=21(ax12+dx22+2bx1x2)
m i n x 1 2 + x 2 2 + x 1 x 2 + 2 x 1 + x 2 s . t . x i ≥ 0 , i = 1 , 2 ∑ i = 1 2 x i = 1 min\,\,x_1^2+x_2^2+x_1x_2+2x_1+x_2\\ s.t.\,\, x_i≥0,i=1,2\\ \sum_{i=1}^2x_i=1 minx12+x22+x1x2+2x1+x2s.t.xi≥0,i=1,2i=1∑2xi=1
因此,由 x 1 2 + x 2 2 + x 1 x 2 x_1^2+x_2^2+x_1x_2 x12+x22+x1x2可以推出:
P = [ 2 1 1 2 ] P=\begin{bmatrix}2&1\\1&2\end{bmatrix} P=[2112]
由 2 x 1 + x 2 2x_1+x_2 2x1+x2可以推出:
q = [ 2 1 ] q=\begin{bmatrix}2\\1\end{bmatrix} q=[21]
注意:约束条件需要化成标准形式:
s . t . − x i ≤ 0 , i = 1 , 2 ∑ i = 1 2 x i = 1 s.t.\,\, -x_i≤0,i=1,2\\ \sum_{i=1}^2x_i=1 s.t.−xi≤0,i=1,2i=1∑2xi=1
因此,可以推出:
G = [ − 1 0 0 − 1 ] h = [ 0 0 ] A = [ 1 1 ] b = 1 \begin{array}{lcl} G=\begin{bmatrix}-1&0\\0&-1\end{bmatrix}\\\\ h=\begin{bmatrix}0\\0\end{bmatrix}\\\\ A=\begin{bmatrix}1&1\end{bmatrix}\\\\ b=1 \end{array} G=[−100−1]h=[00]A=[11]b=1
因此,要求解:
m i n x 1 2 + x 2 2 + x 1 x 2 + 2 x 1 + x 2 s . t . x i ≥ 0 , i = 1 , 2 ∑ i = 1 2 x i = 1 min\,\,x_1^2+x_2^2+x_1x_2+2x_1+x_2\\ s.t.\,\, x_i≥0,i=1,2\\ \sum_{i=1}^2x_i=1 minx12+x22+x1x2+2x1+x2s.t.xi≥0,i=1,2i=1∑2xi=1
可通过:cvxopt.solvers.qp(P,q,G,h,A,b)来进行求解。
其中参数为:
P = [ 2 1 1 2 ] , q = [ 2 1 ] , G = [ − 1 0 0 − 1 ] , h = [ 0 0 ] , A = [ 1 1 ] , b = 1 P=\begin{bmatrix}2&1\\1&2\end{bmatrix},q=\begin{bmatrix}2\\1\end{bmatrix}, G=\begin{bmatrix}-1&0\\0&-1\end{bmatrix},h=\begin{bmatrix}0\\0\end{bmatrix}, A=\begin{bmatrix}1&1\end{bmatrix},b=1 P=[2112],q=[21],G=[−100−1],h=[00],A=[11],b=1
Code:
from cvxopt import solvers, matrix
P=matrix([[2.,1.],[1.,2.]])
q=matrix([2.,1.])
G=matrix([[-1.,0.],[0.,-1.]])
h=matrix([1.,1.])
A=matrix([1.,1.],(1,2))
b=matrix(1.)
solvers.options['show_progress'] = False
sol = solvers.qp(P,q,G,h,A,b)
print(sv['x'])
print(sv['primal objective'])