Python基于机器视觉的图像风格迁移

目 录
1项目背景 4
2相关工作 4
3方法 4
3.1Nerual Style Transfer 4
3.2AdaIN 5
3.3Style Interpolation 5
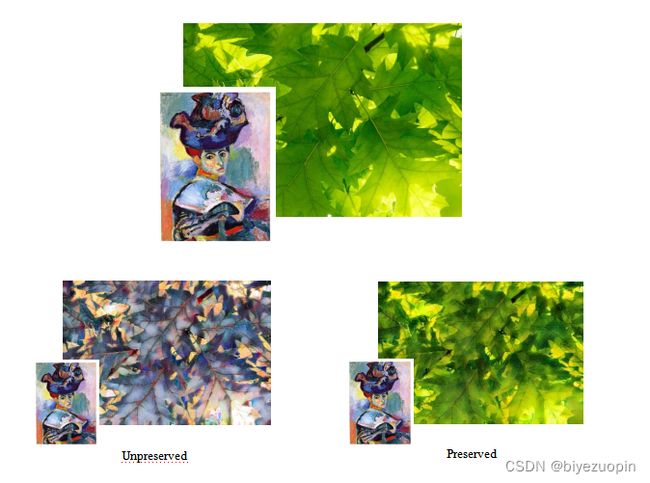
3.4Preserving Color 6
3.5Spacial Control 6
4实验 7
4.1水墨画风格转换（Nerual Style Transfer） 7
4.2水墨画风格转换（AdaIN） 7
4.3Style Interpolation 7
4.4Preserving Color 8
4.5Spacial Control 8
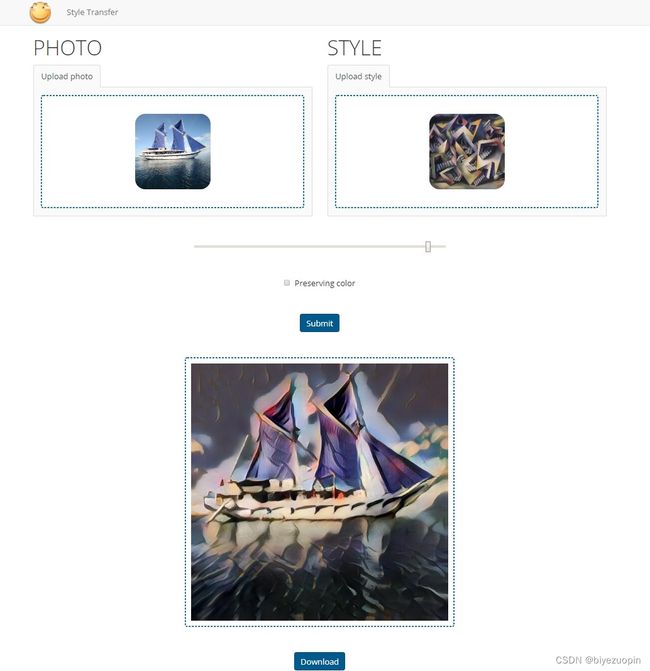
5网页 8
6结论 9
小组分工 9
致谢 10
参考文献 10
1项目背景
风格迁移是计算机视觉的热门话题话题，也被常常被应用于我们的日常生活中，小则包括我们手机相机里的各种滤镜(固定风格)——人物照片转换成素描画、摄影图片转换成油画风格；大则涉及到三次元人物与二次元人物相互转换最新技术。

图像风格迁移作为应用能够增强图片的艺术性，具有美学价值。而作为一种计算机视觉的技术，亦是在学术前辈们的努力下，不断对算法进行精进改良。从固定风格的滤镜，到任意风格的转化，再到加速算法的发明、实现实时转化，对我们有很大的学习意义与参考价值。这在下面的“相关工作”中详细介绍。

2相关工作
发表于16年的《Image Style Transfer Using Convolutional Neural Networks》是图像风格转换的开山鼻祖，Gatys等人首先提出基于CNN的风格迁移方法，其核心是以VGG各层feature
map的Gram矩阵描述风格信息。输入一张随机噪音构成的底图，通过计算风格损失Style Loss和内容损失Content Loss，迭代更新底图，使其风格上与风格图相似，内容上与内容图相似。但是这个方法时间消耗巨大。有很大改进空间。

同年的论文《Perceptual Losses for Real-Time Style Transfer and Super-Resolution》中Johnson等人提出了一个解决风格转换费时比较久的问题的办法，用感知损失函数训练Image Transformation Networks，本文转载自http://www.biyezuopin.vip/onews.asp?id=16778用一次前传代替了多次迭代。算法速度比Gatys的提升数百倍。但
Johnson等人的方法虽然解决了运行效率问题，但是每一个模型只能用于对某一种特定的风格进行迁移，这使得每增添一张新的风格图，就要训练一个全新的模型，成本过高。

为了解决任意风格迁移的问题，各种方法陆陆续续出现了，其中最有名的是发表于17年的
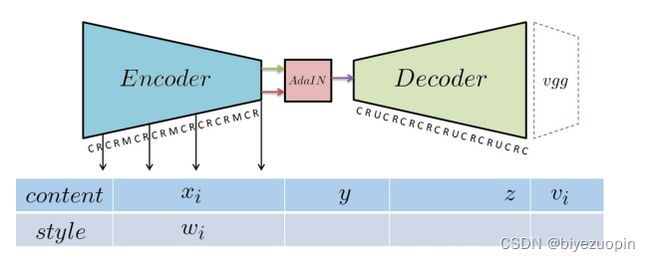
《Arbitrary Style Transfer in Real-time with Adaptive Instance Normalization》，作者创新性地使用了Adaptive Instance Normalization,也就是适应性的IN，以此为基础提出了一种利用自动编码器，能以任意图片作为风格图片的方法。

import torch


def calc_mean_std(feat, eps=1e-5):
    # eps is a small value added to the variance to avoid divide-by-zero.
    size = feat.size()
    assert (len(size) == 4)
    N, C = size[:2]
    feat_var = feat.view(N, C, -1).var(dim=2) + eps
    feat_std = feat_var.sqrt().view(N, C, 1, 1)
    feat_mean = feat.view(N, C, -1).mean(dim=2).view(N, C, 1, 1)
    return feat_mean, feat_std


def adaptive_instance_normalization(content_feat, style_feat):
    assert (content_feat.size()[:2] == style_feat.size()[:2])
    size = content_feat.size()
    style_mean, style_std = calc_mean_std(style_feat)
    content_mean, content_std = calc_mean_std(content_feat)

    normalized_feat = (content_feat - content_mean.expand(
        size)) / content_std.expand(size)
    return normalized_feat * style_std.expand(size) + style_mean.expand(size)


def _calc_feat_flatten_mean_std(feat):
    # takes 3D feat (C, H, W), return mean and std of array within channels
    assert (feat.size()[0] == 3)
    assert (isinstance(feat, torch.FloatTensor))
    feat_flatten = feat.view(3, -1)
    mean = feat_flatten.mean(dim=-1, keepdim=True)
    std = feat_flatten.std(dim=-1, keepdim=True)
    return feat_flatten, mean, std


def _mat_sqrt(x):
    U, D, V = torch.svd(x)
    return torch.mm(torch.mm(U, D.pow(0.5).diag()), V.t())


def coral(source, target):
    # assume both source and target are 3D array (C, H, W)
    # Note: flatten -> f

    source_f, source_f_mean, source_f_std = _calc_feat_flatten_mean_std(source)
    source_f_norm = (source_f - source_f_mean.expand_as(
        source_f)) / source_f_std.expand_as(source_f)
    source_f_cov_eye = \
        torch.mm(source_f_norm, source_f_norm.t()) + torch.eye(3)

    target_f, target_f_mean, target_f_std = _calc_feat_flatten_mean_std(target)
    target_f_norm = (target_f - target_f_mean.expand_as(
        target_f)) / target_f_std.expand_as(target_f)
    target_f_cov_eye = \
        torch.mm(target_f_norm, target_f_norm.t()) + torch.eye(3)

    source_f_norm_transfer = torch.mm(
        _mat_sqrt(target_f_cov_eye),
        torch.mm(torch.inverse(_mat_sqrt(source_f_cov_eye)),
                 source_f_norm)
    )

    source_f_transfer = source_f_norm_transfer * \
                        target_f_std.expand_as(source_f_norm) + \
                        target_f_mean.expand_as(source_f_norm)

    return source_f_transfer.view(source.size())