父视图坐标转换为子视图_简单的数学将简单的2D游戏视图转换为透视3D视图
父视图坐标转换为子视图
透视视角 (Perspective-vue)
Designing a 2D game for a 2D screen is pretty simple to us. But it comes to design a 3D environment for a 2D computer screen we tend to adopt game engines thinking that's a lot of complex math we can't handle. Though there's no denying the reliability of game engines, some features of the 3D environment can be implemented with really simple mathematics we learnt at school. This repository is intented to demonstrate that.
为2D屏幕设计2D游戏对我们来说非常简单。 但是在为2D电脑屏幕设计3D环境时,我们倾向于采用游戏引擎,因为这是我们无法处理的许多复杂数学运算。 尽管不能否认游戏引擎的可靠性,但是3D环境的某些功能可以用我们在学校学到的非常简单的数学来实现。 该存储库旨在证明这一点。
Perspective drawing is a drawing technique used to illustrate dimension through a flat surface. This is how we see a flat surface image and perceive a 3D environment in our brain depending on the position and sizes of the objects drawn. So if we can do the math to calculate how large or small the object needs to be drawn depending on how far it is from the screen, that's all we need to have a 3D layout.
透视图是一种用于说明平面尺寸的绘图技术。 这就是我们看到平面图像并在大脑中感知3D环境的方式,具体取决于绘制对象的位置和大小。 因此,如果我们可以根据距离屏幕的距离进行数学运算来计算需要绘制对象的大小,那么我们就需要3D布局。
入门 (Getting Started)
This is a vue app, clone the repository, set it up, play around.
这是一个Vue应用程序,克隆存储库,进行设置,播放。
项目设置 (Project setup)
yarn install编译和热重装以进行开发 (Compiles and hot-reloads for development)
yarn run serve编译并最小化生产 (Compiles and minifies for production)
yarn run build整理和修复文件 (Lints and fixes files)
yarn run lint数学 (The Math)
Let's see how easy the math is.
让我们看看数学有多么容易。
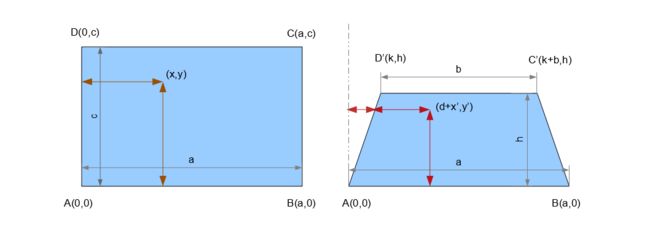
On the left we have a 2D view of a football field and on the right a 3D perspective drawing of the same field. In your mind it has 3 axes (x, y, z) but the paper you would be drawing on has only 2 axes just like the first one and (x', y') is the point on that paper that represents the point (x, y) on the left figure. There is no z-axis on drawing paper, so what appears to be the z-axis on the right figure is actually the y-axis of the paper.
左侧是足球场的2D视图,右侧是同一个足球场的3D透视图。 在您的脑海中,它有3个轴(x, y, z)但是您要绘制的纸张只有2个轴,就像第一个轴一样,并且(x', y')是该纸张上代表该点的点(x, y)在左图。 绘图纸上没有z轴,因此右图上的z轴实际上是纸张的y轴。
So if you look closely the point on the right figure that represents (x, y) is actually (d + x', y') with respect to the drawing paper where d is the displacement due to the shifting of left side of the rectangle from the y-axis.
因此,如果您仔细观察右图上代表(x, y)点实际上是相对于工程图的(d + x', y') ,其中d是矩形矩形左侧移动引起的位移从y轴开始。
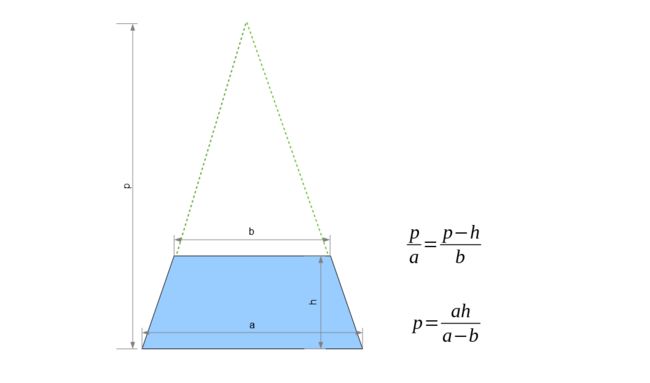
If we extend the unparallel sides of the trapeze backwards they meet at a point of projection P which is at infinity distance from the screen. Say the point is at a height p from x-axis on the drawing paper. We can calculate the length of p from the two similar triangles in the figure below.
如果我们将飞人的不平行的边向后延伸,它们会在投影点P处相遇,而投影点P距屏幕无穷远。 假设该点在绘图纸上距x轴的高度为p 。 我们可以从下图中的两个相似三角形计算p的长度。
Comparing similar triangles we can calculate the value of d from the following figure.
比较相似的三角形,我们可以从下图计算d的值。
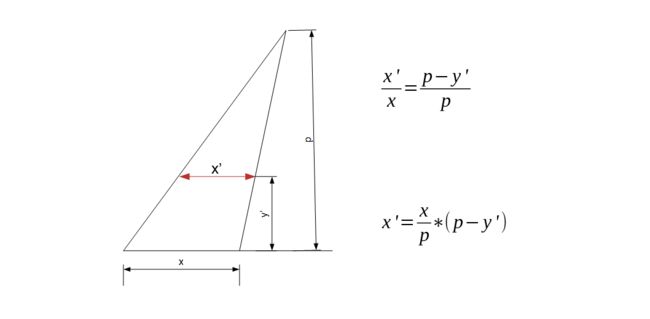
Now let's calculate the size of objects at different distances from the viewer. Any object which appears to be of length x when positioned at the x-asis will appear smaller when we move it away from the screen. Say it appears to be of length x' when positioned at a distance y' from x-axis on the drawing paper (y' is not equal to y, it is the height on the paper where x' is drawn which we will calculate in next step). So we calculate the value of x' at a distance y' comparing the two similar triangles in the following figure.
现在,让我们计算距查看器不同距离的对象的大小。 当我们将其移离屏幕时,任何看起来长度为x对象在x-asis处都会显得较小。 假设当它位于绘图纸上与x轴的距离y'处时,它的长度似乎为x' ( y'不等于y ,它是绘制x'的纸张高度,我们将在其中计算下一步)。 因此,我们比较下图中的两个相似三角形,计算出距离y' x'处的x'值。
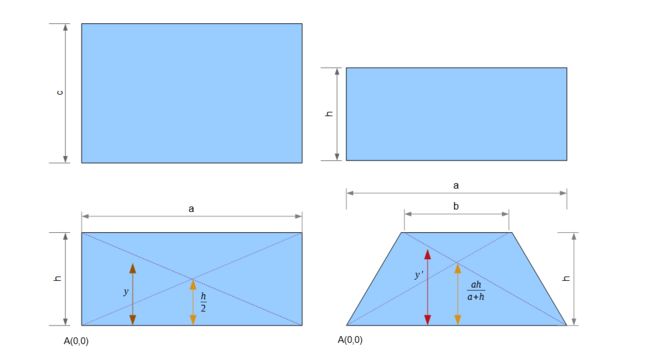
Now calculating the value of y' is slightly complicated. If an object is in the middle of the 2D space, it won't be in the middle of the 3D space drawn on a 2D screen/paper. For better understanding we squeeze the height of the rectangle to match that of the the trapezium. The middle point of both the field is where the diagonals meet and they don't meet at the same height on the drawing paper.
现在,计算y'的值有些复杂。 如果对象在2D空间的中间,则不会在2D屏幕/纸张上绘制的3D空间的中间。 为了更好地理解,我们挤压矩形的高度以匹配梯形的高度。 这两个场的中间点是对角线相交的地方,它们在工程纸上的高度不同。
The following table shows corresponding values of y' with respect to y.
下表显示了相对于y的y'对应值。
| y | y' |
|---|---|
| 0 | 0 |
| h/2 | ah/(a+h) |
| h | h |
| ∞ | p |
| ÿ | ' |
|---|---|
| 0 | 0 |
| h / 2 | ah /(a + h) |
| H | H |
| ∞ | p |
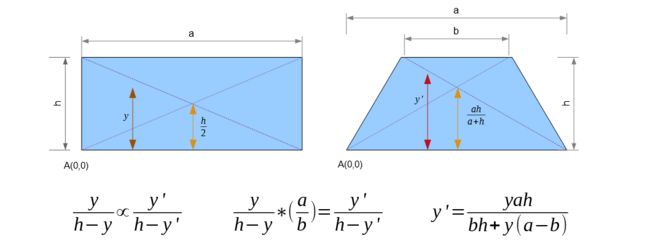
The ratio of distances of y' from a and b is proportional to the lengths of a and b. The relationship is illustrated in the figure below.
的距离之比y'从a和b成比例的长度a和b 。 该关系如下图所示。
This equation satisfies all the corresponding values shown in the table above. If you get stuck verifying the last one, the trick is the term bh is negligible to the term ∞(a-b) and thus can be taken off the equation.
该公式满足上表中显示的所有相应值。 如果您无法验证最后一个,则诀窍是bh项对于∞(ab)可以忽略不计,因此可以从等式中删除。
致谢 (Acknowledgments)
This repository is just intended to demonstrate use of simple math to solve complex looking challenges.
该存储库仅用于演示如何使用简单的数学方法来解决复杂的外观难题。
翻译自: https://vuejsexamples.com/simple-math-to-convert-simple-2d-game-view-to-a-perspective-3d-view/
父视图坐标转换为子视图