一文看懂遗传算法【c/c++实现】
文章目录
-
- 定义:什么是遗传算法?
- 一个帮助理解的例子
- 什么是交叉?
- 什么是局部最优?
- 什么是变异?
- 一个比喻
- 遗传算法整体流程
- 周而复始,如何停下来?——停止条件
- 一个实例
- 第一步 编码
- 第二步 初始化种群
- 第三步 计算种群中个体的适应度
- 第四步 选择
- 第五步 交叉
- 第六步 变异
- 结束条件
- 完整代码
定义:什么是遗传算法?
遗传算法(英语:genetic algorithm (GA) )是计算数学中用于解决最优化的搜索算法,是进化算法的一种。进化算法最初是借鉴了进化生物学中的一些现象而发展起来的,这些现象包括遗传、突变、自然选择以及杂交等等。
以上是维基百科的定义,很宽泛。我这里说人话就是:把数据当做基因片,这些基因片在不断的变化(交叉、变异),在外界筛选下逐步淘汰劣质基因片,最终得到最佳的数据,这就是遗传算法。
首先要说明一点,一般来说,遗传算法不是什么神仙解法,不能求出绝对最优解,求出来的都是相对最优解,也就是和最优解比较靠近,但是一般来说,都并非是最优解。存在一定的误差。除非极少数情况,规则设置得很好,那么也可能求出绝对最优解,但是那都是在一定的时间和大量的试错下完成的。
一个帮助理解的例子
这个东西叫做DNA,生物不好的同学可以看看。这是生物基本的遗传物质之一。
如果我们将其展开来看,把这扭曲的双螺旋拆解开,也就是这样:
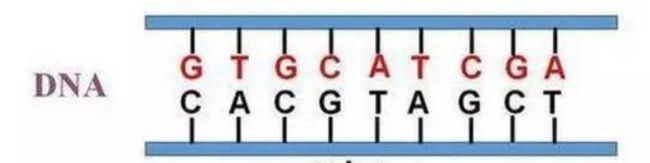
不用管这上面挂的字母都是什么意思,只需要知道这上面每个字母都代表着一些信息。
现在就有了一个重点,如何利用这种基因的模式来表示一个数据呢?
我们只取下面这部分来看:

这里有着A,T,C,G四种模式
如果我不考虑这么多,假设只有两种模式,只有0和1,是不是就和计算机里面的数据表示联系在一起了呢?

你看,就像这样,这个数据就是101101001.如果将这个数看作二进制(电脑使用的数字),就能将其转化为十进制(普通人使用的数字)。我想这个是初中的内容了,如果想知道,可以自行搜索“十进制与二进制的转化”。反过来,十进制也能表示成二进制。
好了,我们已经知道可以把一个数据表示成基因的形式,遗传算法的最开始一部,就是要制造大量的这样的基因。
假设有5个基因片段:

从右边可以看到每个二进制数对应的十进制的数值。
假设我们就是大自然(我既是主宰!!)那么我们只需要从中选择一个我们最想要的数据。没错,在遗传算法中,我们人为的模拟了大自然,然后从中选择我们认可最合适的数据。
如果一条数据(基因)越符合我们的期待(自然环境),我们就说这个数据的符合度(适应度)越高。
例如这里,假设我需要的结果越靠近0越好,于是我认为第2条数据(96)是最优秀的数据,而第5条数据是最差劲的数据(489)。那么我们接下来怎么做呢?
可以采取以下的方案(当然还有更多的其他方案):
1.移除掉第5条数据,再把第2条数据复制一份。这样数据总数还是5条,但是种群中优秀的数据变多了。(这种方法保证了最优的数据必然会留下来,)
2.给这些数据一定的概率,数据越优秀,分配给它的概率点就越大,然后从这些数据中按照概率大小随机抓取5个,抓到谁就把谁留下,否则就剔除掉。(这样即使优秀的数据,也不一定会被保留下来,更加符合自然选择,例如即使含有优秀基因的动物也不一定能存活,但是其存活的概率更大。)
以上过程,模拟了自然选择。
换个角度说,假设数据趋近于0的话,太简单了。如果我们把这个数据设为x(这个x就是刚才的十进制数据),现在有一个函数f(x)=x9-x8+x3-x2,我们要求f(x)取最小值时,x为多少。这样的函数的最小值很难直接看出来,但是我们可以将上面5个数据(即5个x)代入其中,看哪个数据最小,然后不断改变数据,筛选出使得f(x)最小的数据,最后就能得到使得f(x)最接近最小值的x。
在这里,f(x)就是适应度函数。
有了适应度函数,我们就有了目标,只要一直淘汰掉劣质基因,保留优秀的基因,不断向着目标前进,就能达到我们最想要的结果。
可是选择了之后,数据如果不发生改变,那么就没有二次选择了,也就不能朝着0靠近了。所以这里我们需要让其发生变化,以便于第二次选择。具体是哪些变化呢?
可以参考基因片段的变化,主要分为:交叉、变异。
什么是交叉?
基因存在一种交换基因片段的行为,如下图所示:
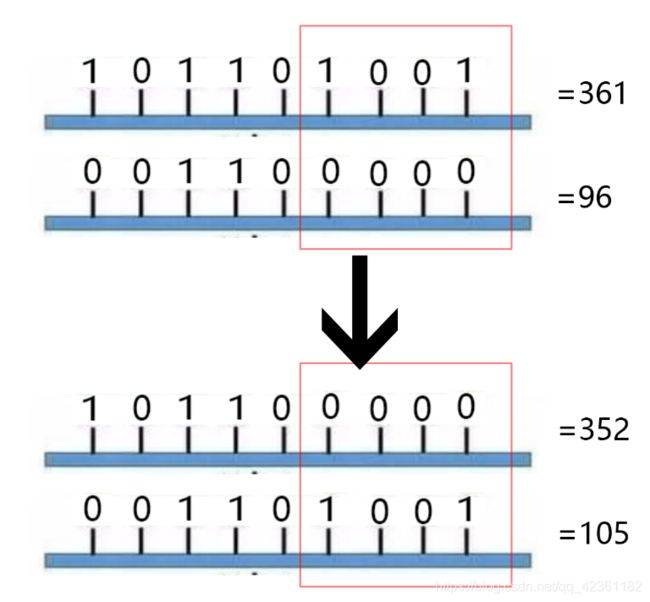
这是第(1)和第(2)条基因交换后四位,就会发生这样的变化,比起最初的数据,我们最初得到的最小值(96)居然因为交叉而变得更大了(变成了105),假设我们还是希望数据越靠近0越好,但这个交叉显然是背离了我们的初衷。由此我们可以得出一个结论:交叉一般是一个随机的过程,并不一定朝着让数据朝着更加符合我们期待的方向变化。其目的是让数据发生大幅度的变化,或者整体性的变化。就好像在直角坐标系中,在每个象限之间跳跃,一跳就是一个象限,这就属于比较大范围的变化,也属于整体性的变化。
交叉的方法可以有很多。
例如可以让前5位交叉,或者第2-4位交叉,或者奇数位交叉,交叉的规则其实是你定的,规则如果定的好,就能使其尽量不陷入局部最优。
什么是局部最优?
看看首先看看这张图,如果我们要求最小值,刚开始的时候,所有的数据站在A点,于是根据我们的交叉变化,就有部分数据站到了D点,接着有更小的数据站到了E点,最后站到了B点,接着怎么变都是B最小。这时候算法就该停下来了。于是我们找到了“局部最优解”,又能叫做近似最优解。这里的B就是我们求得的局部最优。
但是很明显,C才是真正的最优解。如果我们设置的“变化幅度”很大,允许跳跃的横纵距离很大,即允许x变化很大,那么就可能一下子从A点跳跃到G点,接着慢慢靠近C点,而部分数据则会停留在B点,这时候C比B小,因此C才是更加合适的数值。而“交叉”一般在做的事情,就是让数据的变化范围足够大,避免陷入局部最优。
什么是变异?
基因有交叉,也有变异。
变异是指一个基因片段突然发生异变。
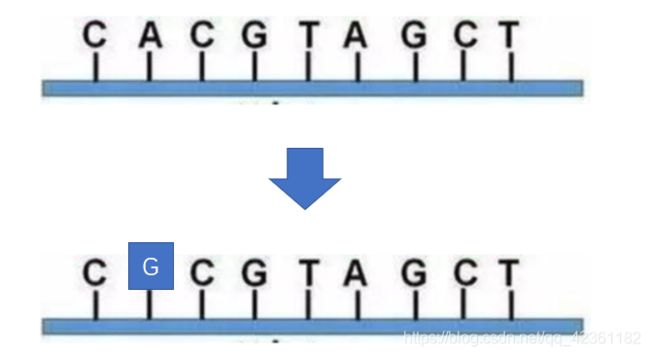
例如这里的碱基中,原来低2个位置的A,突然就变成了G
那么对应到二进制数,也是同样的道理:

例如这里最高位发生了变化,数据就直接变成了233,变化挺大的。

最低位发生变化,数据就变成了360,变化很小。
通过这两个例子就能发现,变异只需要单独一个基因就能完成,而且其变化的幅度可大可小。
对比一下交叉:交叉可以让数据的一部分发生交换,但是数据整体一般之和变化不大。但是变异会让整个数据发生一些突变,整体之和也会变化很大。这就是说,一般情况下,变异改变了整体性质,而交叉维持了整体性质。
一个比喻
如果把这整个遗传算法比作一棵树根,最终我们需要的是树根尽量深的扎入到地下土壤中,但是地下又布满了岩石,因此树根不得不绕道而行,不断曲折向下。这时候,“交叉”就像是长出粗壮的树根,指向某一个方向,而“变异”就像是产生了无数粗细不等的小触须,触摸着地底的岩石外形,最终绕过岩石,向着更深的地方前进。
我们在使用“交叉”维持整体性质的基础上,时不时用“变异”改变一下整体性质,就能越来越靠近期待值。
因此交叉和变异各有用处,但是如果设置得好,交叉与变异可以只取其中一个操作。
遗传算法整体流程
至此。遗传算法的整体流程就已经出来了。
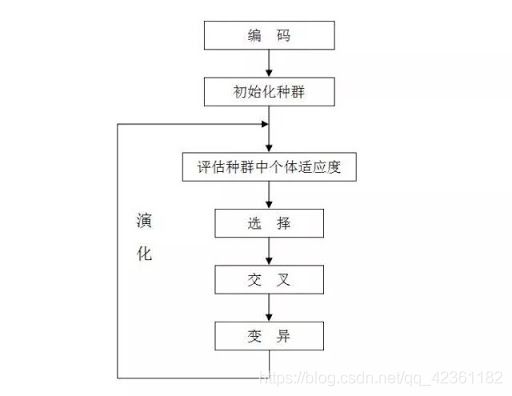
首先是编码,对应到我们的这个例子上,就是把数据用二进制表示,使得数据就像是一条基因片段。
然后是初始化种群,就像我随意列出的5条基因片段。这时候就把种群数量默认为5了。
然后是评估种群中个体适应度,就像我之前说的,判断哪一个数据更加符合你的期待,那个用来判断的函数也就是适应度函数。
然后是选择,我们充当了大自然,通过一些选择的方法,选出更加符合期待的结果。
然后是交叉、变异。
这之后又重复估算适应度。周而复始,最终靠近局部最优解。
周而复始,如何停下来?——停止条件
看到这个遗传算法,就是不断重复,不断的靠近最优解,却无法保证达到最优解,那么如何停下来呢?
1.种群里面只有一种基因了
这种虽然比较少见,但是如果淘汰率比较高,那么还是有可能出现的,其具体情况就是,整个种群,例如有100多条基因,结果因为选择淘汰,全都变成了一模一样的数据。这时候一般来说,就该结束了。
2.种群里面最优的基因长期不变化,或者变化极小
例如种群里面的最优基因,持续了50代,一直都是同一个基因,那我们可以近似认为,这就是我们需要的近似最优解。当然如果这50次最优数据并不相同,但数据的变化极小,例如其方差只有不到10-6(或者你觉得更小或者更大的范围),那我们同样可以认为这50次里面最优的数,就是最优的结果。
3.迭代次数用尽
我们可以设置一个迭代计数器,例如设置为10000.每次完成一次流程,就把计算器-1,如果减到0了,那就结束好了,毕竟都搞了10000次了,再多估计也没有多少意义了。当然这里的次数需要你自己估计,一般来说,迭代次数用尽,是最后的保底手段,因为像以上的几点,可能都会因为你规则设计不好,导致收敛速度相当慢,可能运行很久都不会停下来,但是如果设置了迭代次数,那么到了一定次数必定会停下来。只不过这时候,是否能得到满意的结果,就尚不清楚了。
一个实例
说了这么多,如果不举例子,那也是空话。
现在这里举个例子吧。


高数不懂没关系,至少知道了——因为这里有很多解,所以很麻烦,而且容易陷入局部最优。这时候该怎么求出函数的最大值呢?先画出这个函数来看看。这是[-1,2]区间内的函数。

观察可知这个函数有着很多的极大值点,也就是有着很多小突起,这说明了该函数很容易陷入局部最优。
但是最大值还是能隐约看到,是在x=1.8右边一点。
这时候y值超过了2.5而且靠近3.
现在假设我们不能画出这个图。要用遗传算法求一个最大值,该怎么求呢?
我这里已经写好了遗传算法,然后进行了求解:
运算结果如下:

由此可见,非常接近我们想要的值。遗传算法的确给了一个较好的结果。但是遗传算法具体是怎么做的呢?
第一步 编码
我们需要用一条二进制数来代表一个基因片段。那么为什么要考虑编码呢?
因为这个二进制数据的长度,决定了本次算法的精度。
在此需要解释一下:
1.什么是步长?
假设二进制编码的长度为 N,则说明其可以表示2N个二进制数。
例如3位二进制编码,就可以表示8个二进制数:
000
001
010
011
100
101
110
111
以上合计8个二进制数。8=23
把这2N个二进制数,放置到区间[a,b]的2N个点上。就可以出现如下的情景(假设这里的[a,b]就是[-1,2]):

如图所示,-1到2的区间被划分为8-1=7段。
每一段的长度为(2-(-1))/7=3/7个单位
这里的3/7也就是步长。

再举个例子:

这时候有了步长,步长是影响影响“十进制数与二进制的转化”的。步长代表了x的最小移动,这个移动范围越小,显然求解的精度就越高。因此,步长越小,精度越高。

好了,回到我们刚才的问题:

这里求N的等式,只是把刚才求步长的等式反着写了一次。这样因为我们要求的精度是0.000001,意思是说我们要求的步长是0.000001,由步长,我们就能推出至少需要多少位,此时求得N=22.也就是至少需要22位,将[-1,2]这个区间划分为222 -1个段,每一段长度为7.152559x10-7
由此可以得出,我们的一条基因至少要长度为22位,才能达到精度要求。
第二步 初始化种群
这里要进行遗传算法,先要有一个种群。每一个个体,都是一个长度为22的基因片段,而种群数量则可以自己定。
种群数量越大,其涉及的范围就越广,越不容易陷入局部最优,但是种群数量大,也会导致收敛变慢。
这里我们可以折中选择数量,例如我选择种群数量为50.由此,我们产生了50条长度为22的数据片段,要注意,初始种群一定要随机产生。
第三步 计算种群中个体的适应度
要想计算适应度,首先就要有一个适应度函数。
我们的题目要求是这样的:
很显然,题目中的f(x)就是适应度函数。如果某个个体的适应度越高,就说明该个体越适应环境。
于是带入x就能计算一下这50个个体的适应度。其中x的具体算法,要参照之前步长有关的结论,如下(其中最后面那个符号是指步长):

这样我们就能计算出50个个体的适应度。这些因为是随机的数据,总会有高有低,接下来,我们就要进行“选择”,将适应度高的更大概率留下,适应度低的更大概率淘汰。
第四步 选择
之前我已经列出了一些选择方法。
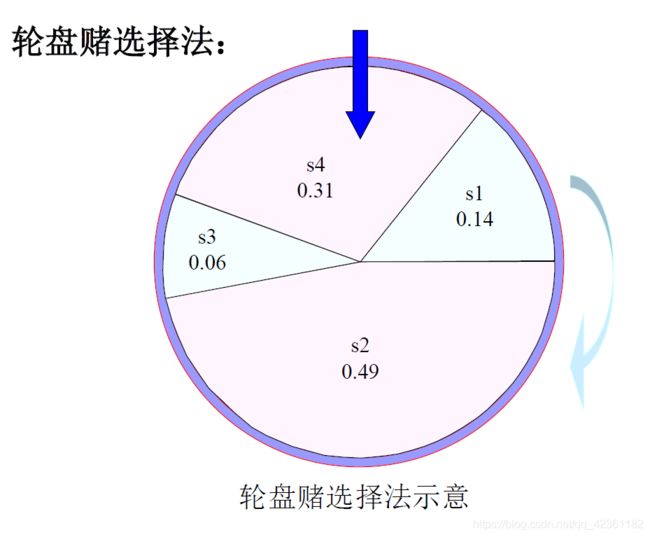
那么这里就推荐一种最常用的选择方法:轮盘赌选择法
为了便于读者观察,我这里把50个个体的种群,先用一个只有4个个体的种群代替。需要注意,这里的思想是一样的,与种群数量无关。
假设我求出了其适应度,如下。(当然这个适应度函数肯定不是上面所说的f(x))
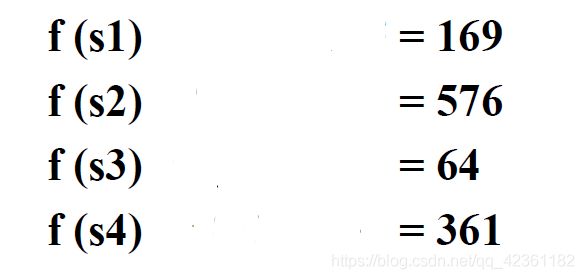
观察可知。显然s2的适应度最高,那么它应该有最大的概率被保留下来。而s3最小,那么其被保留下来的概率也应该最小。
如何确定概率?
这里给出一个概率计算公式

这个公式意思就是:把每个数都除以其总和,就能得到其占据的概率。
总和为169+576+64+361=1170.
P(s1)=169/1170=0.14
P(s2)=576/1170=0.49
P(s3)=64/1170=0.06
P(s4)=361/1170=0.31
这时候,轮盘在转动,停下来之后,随机指向一个,便把该个体抽出来。如果种群数量为4,那么就抽4次,剩下的4个个体,也就是存活个体,这样一来,我们没有让种群数目变大,却让种群向着我们期待的方向进化了。
对应过来,因为我们这里有50个个体,因此我们需要对50个个体全部求出概率,然后进行轮盘筛选。
第五步 交叉
正如我之前所说,交叉是为了让种群发生变化。
而交叉的方法也是自己定的。
我这里就随意选了一种:
首先从种群中随机抽取两个个体,然后这两个个体的任何一位(有22位)都可能发生交叉互换。其交叉互换的概率从高到低依次减小。
第六步 变异
变异也是一个自定义的操作。不同的操作,其效果可能不一样。
我这里选用的方法是:
有一个变异率为0.01,先抛出一个随机数,如果随机数小于了0.01,则说明变异发生了,这时候从种群中随机抽取一个个体,随机改变其中1位即可。
经过了这一步,需要再次计算适应度,再次进行选择。周而复始,直到满足结束条件。
结束条件
我这里的结束条件设置为:150代迭代。
如果超过了150代,则自动结束。
接下来,便是上完整代码了。
完整代码
#include //将X的第Y位置1
#define CLRBIT(x,y) x&=!(unsigned(1)<//将X的第Y位清0
#define REVERSEBIT(x,y) x^=(unsigned(1)<//某一位取反
#define GETBIT(x,y) ((x) >> (y)&unsigned(1))//获取某一位的值
inline double adaptability(double& x) { return x * sin(10 * PI*x)+1.0; }//定义适应度函数
inline double log(double m, double n) { return log(n) / log(m); }//定义log(m,.n)函数
void ExchangeGene(int &a, int &b, int position);
void ExchangeGenes(int &a, int &b, vector<int> list, vector<double> probability);
void Mutation(int &a, int position, double probability);
double range[2] = { -1,2 };//求数值的范围
double delta = 1e-6;//精度误差
int GroupNumber = 50;//种群数量
double Pc = 0.25;//交叉率
double Pm = 0.01;//变异率
int Times = 150;//迭代次数
int main()
{
const int N = int(ceil(log(2, (range[1] - range[0]) / delta)));//基因的位数
const double Step = (range[1] - range[0]) / (pow(2,N)-1);
double random_num;//定义一个随机数
auto *Group = new double[GroupNumber];
auto*Adaptability = new double[GroupNumber];
auto*Probability = new double[GroupNumber];
auto BinaryGroup = new int[GroupNumber];
int i;//循环索引
//初始化
uniform_real_distribution<double> u(range[0], range[1]);//随机数的产生范围
default_random_engine e(time(nullptr));//随机数的种子,用以保证产生的数是随机的
for(i=0;i<GroupNumber;i++)
{
Group[i] = u(e);//种群数据随机初始化
Probability[i] = 0;//将概率数组初始化为0,这个概率是为了方便之后的个体淘汰
}
for(int Time=0;Time<Times;Time++)//迭代次数
{
for (i = 0; i < GroupNumber; i++)
{
Adaptability[i] = adaptability(Group[i]);//计算适应度
}
//数据归一化
const double MaxA = *max_element(Adaptability, Adaptability + GroupNumber);//求出适应度中最大值
const double MinA = *min_element(Adaptability, Adaptability + GroupNumber);//求出适应度中最小值
for (i = 0; i < GroupNumber; i++)
{
if (MaxA == MinA)
{
Adaptability[i] = 1 / GroupNumber;//如果最大最小值相等,即初始情况,需要将适应度全部置为等概率
}
else
{
Adaptability[i] = (Adaptability[i] - MinA) / (MaxA - MinA);//适应度归一化
}
}
double ASum = std::accumulate(Adaptability, Adaptability + GroupNumber, 0.0);//计算适应度之和
for (i = 0; i < GroupNumber; i++)
{
for (int j = 0; j < i; j++)
{
Probability[i] += Adaptability[j];
}
Probability[i] /= ASum;//计算出选择概率,这里使用了轮盘筛选法
}
//种群筛选
uniform_real_distribution<double> u_new(0.0, 1.0);
for (i = 0; i < GroupNumber; i++)//进行GroupNumber次选择
{
random_num = u_new(e);
int index = 0;
while (random_num<Probability[index] || random_num>Probability[index + 1])//当指针落到了第index个扇区之间
{
index++;
if (random_num > Probability[GroupNumber - 1])
{
BinaryGroup[i] = int(ceil(Adaptability[GroupNumber - 1]));//将挑选出的新数组以二进制表示
break;
}
}
BinaryGroup[i] = int(ceil(Group[index] / Step));//将挑选出的新数组以二进制表示
}
//交换基因片段
for (i = 0; i < GroupNumber; i++)
{
random_num = u_new(e);
if (random_num < Pc)
{
const int other = rand() % GroupNumber;//让当前个体与另一随机个体(第other个个体)交换基因片段
vector<int> positions;
vector<double> probability;
for (int h = 0; h < N; h++)//方法一:N个基因均可能发生交换
{
positions.push_back(h);
probability.push_back(double(1) / double(h + 1));//交换的概率由高位到低位,逐渐降低
}
// for(int h=0;h
// {
// positions.push_back(h);
// probability.push_back(1);
// }
ExchangeGenes(BinaryGroup[i], BinaryGroup[other], positions, probability);
}
}
//发生突变
for (i = 0; i < GroupNumber; i++)
{
random_num = u_new(e);
if (random_num < Pm)
{
Mutation(BinaryGroup[i], rand() % N, 1);//随机位置百分百可能突变
}
}
//将二进制数组转化为数字数组
for(i=0;i<GroupNumber;i++)
{
Group[i] = BinaryGroup[i] * Step;
}
// cout << Time << endl;
}
//求出适应度最大的个体
for (i = 0; i < GroupNumber; i++)
{
Adaptability[i] = adaptability(Group[i]);//计算适应度
}
double max_a=Adaptability[0];
int temp_index = 0;
for(i=0;i<GroupNumber;i++)
{
if (Adaptability[i] > max_a)
{
temp_index = i;
max_a = Adaptability[i];
}
}
cout << "num:" << setprecision(10) << Group[temp_index] << endl;
cout << "Adaptability:" << adaptability(Group[temp_index]) << endl;
cout << max_a << endl;
//清除申请的内存
delete[]Group;
delete[]Adaptability;
delete[]Probability;
delete[]BinaryGroup;
return 0;
}
//交换单个基因函数
void ExchangeGene(int &a,int &b,int position)//position从0开始到31
{
//position<32
if((a >> position&1)!= (b >> position&1))//先移位再与运算
{
REVERSEBIT(a, position);
REVERSEBIT(b, position);
}
}
//概率交换指定的基因片段
void ExchangeGenes(int &a,int &b,vector<int> list,vector<double> probability)
{
uniform_real_distribution<double> u(0.0, 1.0);
default_random_engine e(time(nullptr));
double rd;
for(int x=0;x<list.size();++x)
{
rd = u(e);
if(rd<probability[x])
ExchangeGene(a, b, list[x]);
}
}
//基因突变函数
void Mutation(int &a,int position,double probability)
{
uniform_real_distribution<double> u(0.0, 1.0);
default_random_engine e(time(nullptr));
if(u(e)<probability)
REVERSEBIT(a, position);
}
感谢阅读。这个代码可能有一些小问题,希望读者自行更改。
运算结果如下:

当然,遗传算法是一个不稳定的算法,其计算出的结果,可能并不是那么靠近真实数值。这就需要读者们自行更改,尝试,让遗传算法更快的收敛,更加靠近真实数值。
PS:不要以为这样就结束了。遗传算法不仅可以求这样函数的最大最小值的问题,还能用在诸多方面。
其核心是——交叉、变异。
如果我们把每个个体,不将其看做一个二进制代码。而是一个矩阵呢?如果是一个结构体呢?个体又该如何变异?结构体又该如何变异?
遗传算法在解决TSP问题等问题上有着显著功效。大家有兴趣可以继续学习,不要被这个狭隘的遗传算法的例子局限了视野。
万物皆可遗传算法。