【CS231n系列】
Stanford-cs231n课程学习笔记(一)
Stanford课程原版是英文,奈何本人英语菜的一批。原版网站放在下面,xdm可以多多学习。BUT! B站up<同济子豪兄>yyds好吧!!!
Stanford231n
文章目录
- Stanford-cs231n课程学习笔记(一)
- 前言
- 一、传统算法
-
- 最邻近分类器 Nearest Neighbor classifier
- 存在问题
- 二、深度神经网络
-
- 1.线性变换
- 2.梯度下降
-
- 损失函数
- 优化函数
- 总结
前言
刚开始在犹豫‘我一个学搞music的可以学cv嘛?’ 咱就是说,学就完事了。毕竟直接搞music咱也不会啊。
CV是当下人工智能热门领域。计算机视觉领域有许多细分方向:物体检测、图像标注、三维重建、人体姿势识别、图片描述等。
课程主要:使用深度学习 (使用深度神经网络实现机器学习的技术) 解决CV领域的问题,特别是针对图像分类技术等。
子豪兄使用亲切的母语进行讲解,小白极度友好!
实现图像分类技术的方法有很多:
①:使用传统的机器学习算法,也就是文章中提到的线性分类器。如KNN、SVM等方法。通过构造特征,使用算法达到分类效果。
②:采用数据驱动的方式,使神经网络自动学习特征,根据所学到的特征进行分类。
③:当然,现在也有一些迁移学习可以使用少量数据重新训练一个预训练模型,使其达到很好的分类效果。
本文简单记录从课程中学到的前两种方法。
一、传统算法
传统算法包括KNN、SVM、决策树等算法,可以很简单的从sklearn库中进行调用,现在通常运用在一些数据分析中。这些算法构造的线性分类器(线性分类器 – 决策边界是特征的线性函数的分类器)如何进行图片的分类?
最邻近分类器 Nearest Neighbor classifier
最邻近算法:找到最邻近的样本的分类,利用‘近朱者赤’原则,进行新样本的归类。
K-NN算法,多找几个人!K个人!一个人容易产生误差!
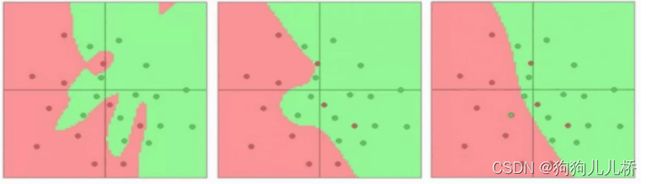
图片展示的使使用knn进行二分类,通过人工构造的特征空间,将样本在空间中进行映射,形成不同的分布,最终根据分布,模型产生一个最优的分解面,对新样本进行分类。KNN是使用样本之间的垂直平分线的组合进行边界的划分。
对于图像分类操作步骤如下:
第一步:首先使用像素点分布,将图片映射到空间中。(train)
补充一点我不会的知识:一个视觉单位取值范围为0~255、8bit表示一个像素点、3通道RGB 通常用一个网格表示
第二步:进行样本之间的距离计算。(test)
计算样本之间的距离通常使用:
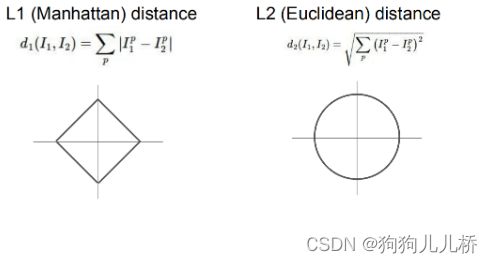
L1距离<曼哈顿距离、L1范数>:求和-对应位置差的绝对值 与坐标系关系比较密切、特征之间有明确的语义
L2距离:<欧氏距离> :高中两点距离公式,圆上距离圆点的距离都相同
需要计算每一个待分类样本和分布空间各个点的距离。通常具有很高的时间复杂度。
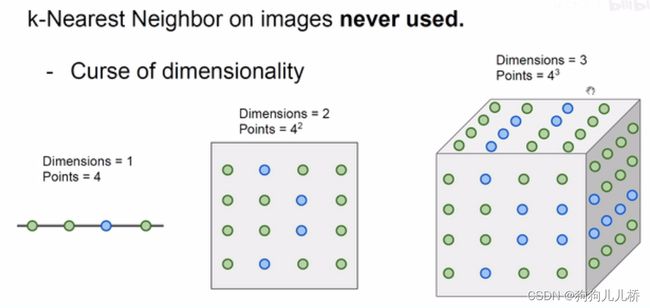
听起来似乎很好理解,解释性也较强,但是存在一个问题,这种分类是否具有较高的可信度?

图片展示的是使用L2距离进行变换后的图片和原图的比较,在故意设计下,后三张变换过后的图片和原图具有相同的L2距离。可见,使用L2距离简单的进行计算像素之间的距离进行分类,可靠性不强。
同时,在随着样本维度的升高,逐渐出现空间维度爆照等问题。
因此我们可以发现KNN具有以下优缺点:
优点:简单,易于理解,易于实现,无需估计参数,无需训练适合对稀有事件进行分类特别适合于多分类问题(multi-modal,对象具有多个类别标签)。
缺点:懒惰算法,对测试样本分类时的计算量大,内存开销大,评分慢可解释性较差,无法给出累决策树的规则。
在日常生活中,仍然有用到KNN的地方。如我们常见的推荐算法,通常根据余弦相似度、L距离等计算用户之间、商品之间某些特征的距离,进行推荐。(用户注册时的标签选择就是为了一定程度上解决推荐算法的冷启动问题)
存在问题
上面我们提到,使用像素不能很好的进行图片的描述,进而分类器效果也不理想。如果我们采用一种对于物体的某些特征进行描述,是否会更好的分类呢?比如,猫咪:两只尖尖的耳朵、胡子等
问题又出现,猫咪有很多种,同时世界上还有很多生物,我们无法做到每一个都达到细粒度划分。
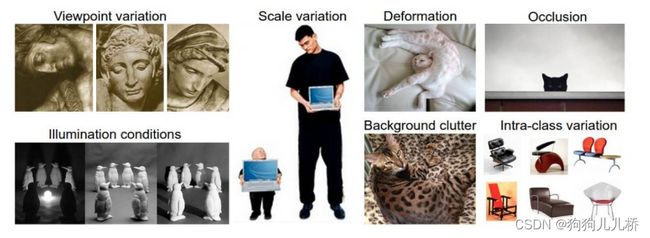
这时,我们便需要使用深度神经网络,帮助我们学习到图片中的某些特征,进而根据自己所学到的特征,进行新样本的分类。
二、深度神经网络
神经网络在很早就被提出,但是当时的CPU算力有限,没有使人们注意到这块金子!
1.线性变换
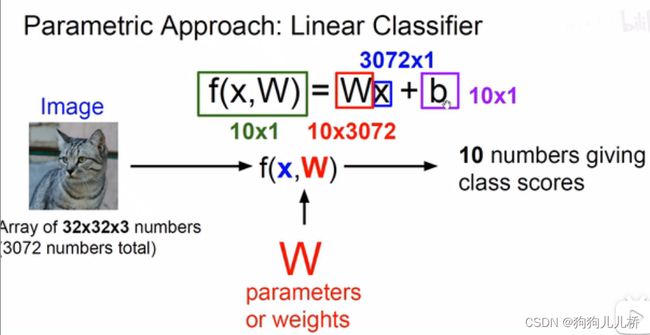
线性分类器和我们学习的初等函数中的线性函数相似,其中W表示权重(是一个分类数*特征的矩阵),b表示偏差。构造分界面,能够将样本进行分类。其中10表示最终分类类别数,3072(32 * 32 * 3)表示特征数

通过矩阵乘法,计算出每一个类别所获得的分数。分数最高的类别即为分类类别。
2.梯度下降
在随机初始化的W和b,得到的分类结果几乎没有什么卵用。我们如何进行参数更新,使其能够好起来?
损失函数
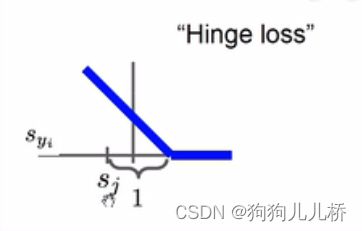
在给定的数据集中,计算模型分类标签和真是标签之间的差距,也就是我们所说的损失。

图片所示的是SVM中用到的损失,也称为铰链损失。
当然还有多种损失函数L1、L2损失、 交叉熵损失函数、最大似然估计(某种时间发生的概率最大)、KL散度
等。(留个坑!明天一定补!!!)
优化函数
损失过大,要用优化。通过计算梯度,找到能够使Loss最小的地方。

数值方法可以帮助我们求梯度,但是存在计算很慢的问题。采用解析解方法进行梯度计算。
优化函数本质:根据各个特征值的变化对于最终Loss的影响,计算梯度,使用梯度下降,使Loss的值逐渐变小。为什么可以通过选择合适的优化函数,使用梯度下降方法进行优化?
是因为Loss通常为非凸函数,可以使用优化方法找到其中的局部最优点、全局最优点,以降低Loss损失。
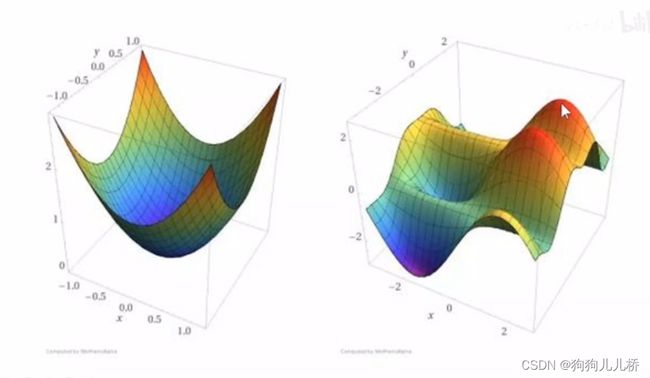
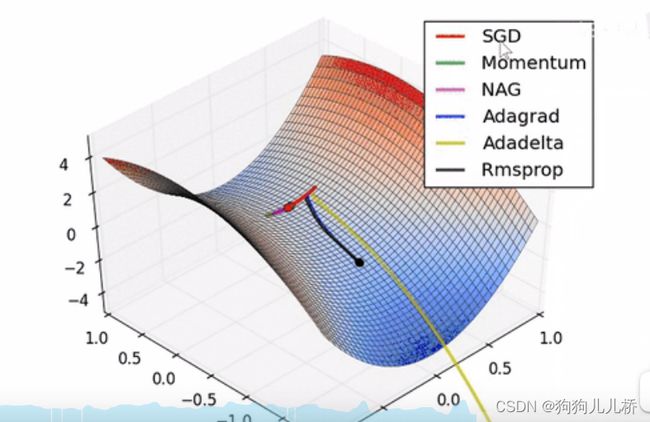
从图中可以看出,不同的优化函数所产生的优化效果不同。
同时,梯度下降过程中,除了选择合适的优化函数,还需要选择合适的学习率(lr):
lr过小:更新的速度过慢。
lr过大:导致出现震荡现象,不能够达到最后的收敛。
同时还有batch-size的选择问题:
batch-size太大:内存问题、全局梯度计算过慢。
batch-size太小:收敛速度太慢。
总结
提示:*******softmax、正则化明天留着补天******