图论知识及其应用初步调研

图论及其应用调研

图论基础

图的分类

• 有向图和无向图
• 有权图和无权图
• 连通图和非连通图

基础知识

• 度：对于无向图，顶点的度表示以该顶点作为一个端点的边的数目。对于有向图，顶点的度分为入度和出度。入度表示以该顶点为终点的入边数目，出度是以该顶点为起点的出边数目，该顶点的度等于其入度和出度之和。
• 生成树：在含有原图所有顶点的前提下，以最少数量的边将它们连接起来，统一生成树，最小生成树
• 拓扑排序：是一个有向无环图（DAG）的所有顶点的线性序列。且该序列必须满足条件，每个顶点出现且只出现一次，若存在一条从顶点 A 到顶点 B 的路径，那么在序列中顶点 A 出现在顶点 B 的前面。通常用来“排序”具有依赖关系的任务。
• 连通性：在图论中，连通图基于连通的概念。在一个无向图 $G$中，若从顶点$i$ 到顶点$j$有路径相连，则称$i$ 和 $j$ 是连通的。如果$G$是有向图，那么连接$i$和$j$的路径中所有的边都必须同向。如果图中任意两点都是连通的，那么图被称作连通图。如果此图是有向图，则称为强连通图。图的连通性是图的基本性质。
• 完全图：一个简单的无向图，其中每对不同的顶点之间都恰连有一条边相连。

图论应用

概述

图可用于在物理、生物、社会和信息系统中建模许多类型的关系和过程，许多实际问题可以用图来表示。因此，图论成为运筹学、控制论、信息论、网络理论、博弈论、物理学、化学、生物学、社会科学、语言学、计算机科学等众多学科强有力的数学工具。在强调其应用于现实世界的系统时，网络有时被定义为一个图，其中属性(例如名称)之间的关系以节点和或边的形式关联起来。

对现实生活中的场景抽象建模，再结合图论相关算法与知识解决实际问题

分述

计算机科学

图被用来表示通信网络、数据组织、计算设备、程序执行流程、芯片设计等

网站的链接结构可以用一个有向图表示，其中顶点表示网页，有向边表示从一个页面到另一个页面的链接

语言学

各种形式的图论方法已证明在语言学中特别有用，因为自然语言常常适合于离散结构。传统上，语法和组合语义遵循基于树的结构，其表达能力取决于组合原则，在层次图中建模。更现代的方法，如头驱短语结构语法，使用类型化特征结构对自然语言的语法建模，这些特征结构是有向无环图。在词汇语义学中，特别是在计算机上，当一个给定的单词被相关的单词理解时，建模单词的意义就更加容易了。因此，语义网络在计算语言学中非常重要。音系学中的其他方法(例如，使用格点图的最优性理论)和形态学(例如，使用有限状态形态学，使用有限状态传感器)在语言作为图的分析中也很常见。如TextGraphs、WordNet与VerbNet等

物理与化学

图论也被用来研究化学和物理中的分子。在凝聚态物理中，通过收集与原子拓扑有关的图论性质的统计量，可以定量地研究复杂的模拟原子结构的三维结构。此外，“费曼图和计算规则将量子场论总结成一种与人们想要理解的实验数字密切相关的形式。”

在化学中，图是分子的自然模型，顶点表示原子，边表示键。这种方法特别用于分子结构的计算机处理，从化学编辑器到数据库搜索。

在统计物理学中，图可以表示系统相互作用部分之间的局部连接，以及系统上物理过程的动态。

类似地，在计算神经科学中，图可以用来表示大脑区域之间的功能连接，这些区域相互作用产生各种认知过程，其中顶点代表大脑的不同区域，而边缘代表这些区域之间的连接。

图论在电气网络的电气建模中起着重要的作用，在这里，权值与线段的电阻有关，从而获得网络结构的电气特性。用图表示多孔介质的微尺度通道，其中顶点表示孔隙，边表示连接孔隙的较小通道。化学图论利用分子图作为分子模型的一种方法。

社会科学

类似莫雷诺社会图的使用使得图论也被广泛地应用于社会学中，作为一种衡量演员声望或探索谣言传播的方法，特别是通过使用社会网络分析软件。在社交网络的保护伞下，有许多不同类型的图。熟人图和友谊图描述了人们是否互相认识。影响图是一种模型，用来描述某个人是否能够影响其他人的行为。最后，协作图建模两个人是否以特定的方式一起工作，例如一起在电影中表演。

生物学

图论在生物学和保护工作中也很有用，其中一个顶点可以表示某些物种存在(或栖息)的区域，而边缘则表示这些区域之间的迁移路径或移动。当观察繁殖模式或跟踪疾病、寄生虫的传播或运动的变化如何影响其他物种时，这些信息非常重要。图论也被用于连接学;神经系统可以被看作是一个图，其中节点是神经元，边缘是它们之间的连接。图论可用于神经网络建模与脑区活动

数学

在数学中，图形在几何学和拓扑的某些部分如结理论中是有用的。代数图论与群论有着密切的联系。代数图论已经应用于包括动态系统和复杂性在内的许多领域。

金融

金融系统可被视为一组相互关联的经济主体，如零售、投资银行、保险公司、投资基金、中央银行、监管机构、金融科技公司、非金融公司和家庭等。这些经济主体之间的关系通常通过合同正式确定，如贷款（两家银行之间，或银行借贷给公司，或银行借贷给家庭）、互惠所有权或保险单。但这种关系也可以是隐性的，比如不同主体对同一种资产的投资就构成了一种间接关系。因此，将金融系统表示为一个网络是很自然的，在这个网络中，节点代表经济主体，连边代表它们之间的关系。在一对主体之间，通常有几种随时间变化的关系。因此，金融系统最真实的表现形式是时序多层网络（temporal multiplex network）。然而，在许多情况下，人们关注的是单个过程，其时间尺度比这些关系变化的时间尺度短得多。这种简化使得将金融系统表示为单层静态网络成为可能。将金融系统表示为一个网络，可以对主体之间的冲击传播进行显式建模。

金融系统网络建模对于捕捉金融机构之间的复杂关系至关重要。金融网络展示了金融系统中有大量重要现象可以从金融行为者之间的相互作用来理解。例如，如果某项资产的价格暴跌，不仅会影响那些投资于该资产的投资者，还会影响那些投资于这些投资者债务的债权人。由于存在错综复杂的契约链和反馈机制，由此产生的影响可能比最初的冲击大得多。与复杂系统的其他领域一样，系统层面不稳定性的出现能从网络结构（例如：封闭链）及其连边和节点的关键属性（例如：与风险传播和财务杠杆有关的属性）的相互作用中理解。

尽管我们都知道丰富的数据集对许多领域复杂系统的研究有巨大帮助，但由于保密问题，金融网络上的分类数据往往无法获得。学者们尝试从部分信息中估计金融网络的结构来解决这个问题，并通过网络结构的变化来识别不稳定的预警信号。

在金融交易的过程中构成交易图谱，使得图论的相关算法具有与金融网络十分相符，随着区块链的普及，在区块链结构上的交易日益增多，更使得隐私诉求显得更加重要。

规划

政府或公司可以用图论进行道路交通规划或者路径优化，加权的边可以表示限速或者车道的数量。建模人员可以用这个系统来判断最佳路线及最有可能堵车的街道。

航空公司可以用图来为其飞行系统建模。将每个机场看成顶点，将经过两个顶点的每条航线看作一条边。加权的边可以看作从一个机场到另一个机场的航班成本，或两个机场之间的距离。

其他

在调研过程中，还发现了网络科学这门分支学科，其致力于研究复杂网络的性质，并且应用这些性质去研究一些具有网络特点的领域，比如信息技术网络，计算机网络，生物圈网络，学习和认知网络，社会关系网络以及经济和金融网络。和图论这个领域关联性较大。还有图形数据库相关领域也是图论实际运用的绝佳场景

图数据库

解决问题

知识内容	具体算法	应用	经典问题
图基本概念与算法	图的表示、图的遍历（广度+深度）、图的环或圈检测、拓扑排序算法	构成图论的基本内容，存储，基本遍历搜索与拓扑排序	遍历搜索，处理有前后关联的任务安排
距离与连通性	最短路径算法、 图连通性判断算法	路径规划、统筹规划与系统可靠性检验	路径规划，设施布局，网络可靠性检测
图着色	解决涂色问题（Welch-Powell算法）	解决资源有限和其他约束条件下的分配问题	课程表问题，安全装箱问题，地图着色问题，信道分配问题
可平面性	判断是否为平面图（DMP算法，平面嵌入的灌木生长算法，PFA,st编码算法）	一个图可以画成任意两条边都不相交的样子，多用于工程规划领域	印制电路板，道路布局
欧拉图与哈密顿图	求解欧拉回路（Hierholzer、Fleury、DFS搜索）、判别欧拉回路，求解哈密顿圈问题	是否/如何遍历所有路径/节点并避免重复	中国邮递员问题，七桥问题
有向图与网络	最大流算法(2F算法，分层算法，Edmond-Karp 算法)，极大流算法，有上下界网络最大流算法，有供需要求的网络流算法	优化调度分配	交通网络调度
树与二分图	最小生成树(DFS+BFS),最优树算法(Kruskal算法)、有序二元树	几乎所有图论都离不开树	Huffman编码；最佳追捕问题
匹配理论	匈牙利算法、求最佳匹配的有效算法、KM算法	在匹配与许配问题中进行最优化处理	BernoulliEuler错插信笺问题；Hall婚配定理；应聘问题
图支配问题	支配树构造(Lengauer Tarjan 算法)	对影响与覆盖问题的数学抽象	皇后问题，中心台站选址

特殊图

“以一种特殊方式对图进行遍历，有时我们需要经过每一条边一次，有时候我们需要经过每一个结点恰好一次”

术语

欧拉图：遍历每一条边一次并恰好再次回到出发点，G是欧拉图当且仅当G是连通的且每个结点的度为偶数

哈密顿图：通过图G的每个结点一次，且仅一次的通路（回路），就是哈密顿通路（回路）。存在哈密顿回路的图就是哈密顿图。与欧拉图的情形不同，还未找到判断一个图是否是哈密顿图的非平凡的充要条件。事实上这是图论中尚未解决的主要问题之一

多重图：允许出现多重边的结构称为多重图

相关算法

判别欧拉回路

无向图G存在欧拉通路的充要条件是：

G为连通图，并且G仅有两个奇度结点（度数为奇数的顶点）或者无奇度结点。

推论1：

1. 当G是仅有两个奇度结点的连通图时，G的欧拉通路必以此两个结点为端点。

2. 当G是无奇度结点的连通图时，G必有欧拉回路。

3. G为欧拉图（存在欧拉回路）的充分必要条件是G为无奇度结点的连通图。

有向图D存在欧拉通路的充要条件是：

D为有向图，D的基图连通，并且所有顶点的出度与入度都相等；或者除两个顶点外，其余顶点的出度与入度都相等，而这两个顶点中一个顶点的出度与入度之差为1，另一个顶点的出度与入度之差为-1。

推论2：

1. 当D除出、入度之差为1，-1的两个顶点之外，其余顶点的出度与入度都相等时，D的有向欧拉通路必以出、入度之差为1的顶点作为始点，以出、入度之差为-1的顶点作为终点。
2. 当D的所有顶点的出、入度都相等时，D中存在有向欧拉回路。
3. 有向图D为有向欧拉图的充分必要条件是D的基图为连通图，并且所有顶点的出、入度都相等。

A.判断欧拉通路是否存在的方法

有向图：图连通，有一个顶点出度大入度1，有一个顶点入度大出度1，其余都是出度=入度。

无向图：图连通，只有两个顶点是奇数度，其余都是偶数度的。

B.判断欧拉回路是否存在的方法

有向图：图连通，所有的顶点出度=入度。

无向图：图连通，所有顶点都是偶数度。

求欧拉回路或欧拉路

Hierholzer 算法

也称逐步插入回路法。

算法流程为从一条回路开始，每次任取一条目前回路中的点，将其替换为一条简单回路，以此寻找到一条欧拉回路。如果从路开始的话，就可以寻找到一条欧拉路。

Hierholzer 算法的暴力实现如下：

Fleury 算法

也称避桥法，是一个偏暴力的算法。算法流程为每次选择下一条边的时候优先选择不是桥的边。

最简单的实现方法是每次删除一条边之后，运行一遍 Tarjan 找桥。复杂的实现方法要用到动态图等，实用价值不高。

DFS搜索求解欧拉回路

基本思路：利用欧拉定理判断出一个图存在欧拉回路或欧拉通路后，选择一个正确的起始顶点，用DFS算法遍历所有的边（每一条边只遍历一次），遇到走不通就回退。在搜索前进方向上将遍历过的边按顺序记录下来。这组边的排列就组成了一条欧拉通路或回路。

哈密顿图算法

一般地，寻找一个图的哈密顿圈问题是 NP 困难的。因此通常都是用穷举搜索的方法来判定一个图是否含有哈密顿路或圈。后来F.Rubin利用推演的方法给出了一个好一点的搜索步骤来找出图里的一些或者全部的哈密顿路或圈，D.Angluin和L.G.Valiant设计的概率算法对哈密顿路或圈的寻找也是非常有用的。寻找哈密顿路的确定算法虽然很难有多项式时间的，但是这并不意味着只能进行时间复杂度为$O(n!\cdot n)$ 暴力搜索。利用状态压缩动态规划，我们可以将时间复杂度降低到$O(n^2\cdot n^3)$ ，具体算法是建立方程$f[i][S][j]$，表示经过了$i$个节点，节点都是集合$S$的，到达节点$j$时的最短路径。每次我们都按照点$j$所连的节点进行转移。

具体应用场景

路径规划–如何遍历所有需要路径并避免重复路径

以经典哥尼斯堡七桥问题为例

在实际生活中可以用于为邮递车、垃圾回收车、扫雪车。旅游路径规划、送牛奶等等设计合适的路线、一笔画问题

哈密顿图及其判定方法可以解决中国邮路问题、旅行售货员问题、排座位问题。

隐私需求

由于涉及到路径，其在现实生活中具有大量具体的隐私需求

举例：

• 我们希望得到自己游园的最佳路径，但不想暴露路径信息

• 在网络中避免重复的遍历所有路径，隐私数据的传输

• 交易图谱中的一笔画问题

例如：

• 输入数据：地图中的某部分“图”（点+线）
• 输出数据：反馈路径执行
• 优化：加入权重，动态调整
• 举例：运钞车需要在几个节点间运送钞票，设计合适的路线并保护隐私；交易图谱中寻找最佳遍历情况
• 评述：欧拉图属于路径规划中的一个分支，算是特殊的最短路问题，特殊的最佳遍历问题

图着色-GCP

“事物基本属性要求它们之间相互隔离”

术语

可k着色：可以用k种颜色着色的图

色数：完成图着色的最小颜色数

独立：S为V(G)的子集，如果S中的任何一对结点都不相邻，则S是独立的

四色定理：任意一个平面图，都可以使用四种颜色进行着色，使得一个结点和它的邻居颜色不一样。四色定理只适合于平面图。

顶点着色：任意一个结点，它的邻居的结点颜色不能和它一样。也就是说，同一条边的两个结点颜色不一样。顶点着色是图着色的基础。点着色要求图不能有自环，就是不能存在两个端点一样的边。但是图可以是多重图。

• 应用：有n个物品需要装箱，有些物品不能放在一起，哪些物品不能放一起都已经知道，求最少需要多少个箱子？问题同样可以描述为有n个动物放到笼子里，或者有n个学生分班。
• 解决：这个问题可以转化成顶点着色问题。假设n个物品为一个图的顶点，如果物品a和b不能在一起，那么就在a和b之间连一条边，问题变成求这个图的点着色的色数。

边着色：任意相邻的边的颜色不能相同，也就是有公共结点的边颜色不能相同。边着色要求图不能有自环，但是可以是多重图。

• 应用：会议安排–全校老师要求各教师每周给某班级上课，问如何安排一张周课程表，使所排课时数目尽可能地少？
• 解决：对图进行边着色，如果两条边颜色相同，就代表它们是同一个时间段。一个老师发出的边不可能相同，一个班级发出的边颜色也不能相同，就是边着色，求出最小色数即可

星着色：一个结点与它的邻居不能同色，一个结点的邻居不能同色

• 应用：溯源–查找IP包经过的路由器，并尽可能少的信息
• 解决：对网络进行星着色，如果我们知道一个IP包经过的路由器的颜色序列以及知道包走过的最后一个路由器，那么我们就能把整个路径找出来

Distance-k着色：任意长度为k(结点数为k+1)的路径，结点颜色都不相同，星着色便是distance-2 Coloring

• 应用：波长分配–主管部门对每家电视发射台分配一个频道。为了排除干扰，使用同一频道的发射台之间相距必须大于指定的正数d
• 解决：典型Distance-k着色问题，保证任意长度为k的路径，结点颜色都不相同

应用

• 调度问题：频道分配，会议/赛事安排，考试日程

• 地图着色

• 动物园设计

• 化学品存放

• 数独问题：数独是图着色问题的一个变种，其中每个单元格代表一个顶点。如果两个顶点在同一行、列和块中，则在这两个顶点内形成一条边，每个块将有不同的颜色。

• 寄存器分配：编译器是将源代码从高级语言（Java、Scala）转换成机器代码的程序。这通常是分步骤进行的，最后一步是将寄存器分配给程序中最常用的值，同时将其它值放入内存。我们可以将符号寄存器（变量）建模为顶点，如果同时需要两个变量，则形成一条边。如果该图可以用 K 色进行着色，那么变量可以存储在 k 寄存器中。

算法

贪心策略：解决图着色问题。虽然它不保证最小颜色数量，但它保证了分配给图形的颜色数量上限

Welch-Powell算法：保证最小数量着色

分析总结

图着色算法用于解决资源有限和其他约束条件的问题。颜色是试图优化的任何资源的抽象，图则是对问题的抽象。

隐私需求

多方共同规划行程安排？

医院病患咨询安排？

提供隐私溯源的记录方法？

对隐私计算过程中的有限约束条件问题提供优化

可平面图

术语

可平面：能将图在平面画出且其边各不相交，所有树都是可平面的，验证这一点的方法就是将树以有根树的形式画出来

交叉数：如果一个图不可平面，最小的边相交次数叫做交叉数

平面图：已经画在平面内且边各不相交的图

算法

平面性算法

判定一个给定图是否为可平面图，并且求出它的一个平面嵌入(若是可平面图)在计算机上可以实现的方法。

第一个平面性算法是由奥斯兰德尔(Auslander，L.)和帕特尔(Parter，S.V.)于20世纪60年代初给出的。之后，出现了有数十种之多的算法。直到1974年，由候波科劳(Hopcroft，J.)和塔尔金(Tarjan，R.)建立了第一个线性时间的算法，即对很大的图这个算法所需的计算时间以图的顶点数的一个线性函数为上界。

例如：DMP算法

应用

• 印制电路板
• 矿洞中的轨道部署与铁路轨道部署
• 场地布局中的邻接关系：在图书馆、医院、商业区等场景进行布局时，希望确保某些区域与另一些区域相邻
• 运筹学中指定两区域邻接关系，并且指定两者的距离，在尽可能满足距离约束的前提下，所有距离之和最小

分析总结

一个图可以画成任意两条边都不相交的样子

隐私需求

许多电路排版设计商业机密，对于所需计算量较大的复杂电路排版需要在隐私下进行计算

与运筹学相互结合实现在隐私条件下的高效分配

距离与连通性

术语

结点的偏心距: 该节点与它相距最远的结点间的距离

图的半径(radius): 所有节点中最小偏心距

图的中心(center): 具有最小偏心距的结点所成集合

图的边界(boundary): 具有最大偏心距的结点所成集合

图的直径(diameter): 所有结点中的最大偏心距

割点: 若G是连通图, 删除其中某结点之后G变为非连通图, 被删除的结点即割点.(对非连通图来说, 删除某节点之后增加了连通分量数目也称为割点)

割边(桥): 删除某边之后连通分量数目增加, 该边为割边.

图的点连通度: 把图变为非连通图或者平凡图至少需要删除的结点数目

图的点割集: 把图变成非连通图所需要删除的结点组成的集合.

应用

• F-图：运用F-图对公路系统进行建模，不同的应急设施应放置在相应尽可能远的地方。例如：当消防车和救护车同时针对不同地点运作时，使用F-图减少途中干扰的可能性（表示中心节点相距尽可能的远）
• 网络可靠性：通信网等对某个组成部分崩溃的容忍度

分析总结

多用于统筹规划与系统可靠性检验

隐私需求

在隐私诉求下，对系统进行结构检测与可信性分析；在隐私诉求下，实现系统优化布局

数据结构与算法

图是一种复杂的非线性结构。

在线性结构中，数据元素之间满足唯一的线性关系，每个数据元素(除第一个和最后一个外)只有一个直接前趋和一个直接后继；

在树形结构中，数据元素之间有着明显的层次关系，并且每个数据元素只与上一层中的一个元素(parent node)及下一层的多个元素(孩子节点)相关；

而在图形结构中，节点之间的关系是任意的，图中任意两个数据元素之间都有可能相关。

邻接矩阵

对于邻接矩阵，一般是针对稠密图，比如完全图，它使用一个二维数组表示，此时空间需求为 $V^2$，如下图是一个邻接矩阵

对于$A[u][v]=value$，表示顶点u和v连接的边

对于无向图, $value=1$表示顶点$u$和$v$有一条边连接，同时$A[v][u]=1$

对于有向图，$value=1$表示以$u$为起点，$v$为终点的边

对于有权图，$value=weight$为权值，可以使用很大或很小的权值表示不存在的边，如0、infinity

邻接矩阵删除和插入边时间为O(1)

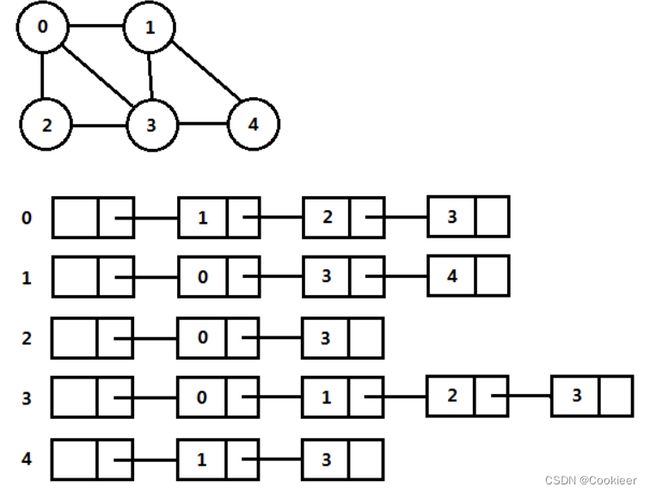
邻接表

一般来说针对稀疏图，该方式使用一个邻接表数组$list[V]$表示图，也就是对于每个顶点，使用一个表存放与该顶点邻接的所有顶点，一共有$V$个顶点，空间需求为$V+E$，邻接表的实例如下图：

如果边有权值，可以在表中每一个单元额外存储权值信息，可以使用一个Pair结构体表示

如上图，图G实际是一个邻接表数组，横向存储的顶点是与一个顶点邻接的，该组合为一个邻接表，整体上可以使用一个数组，邻接表根据使用不用的语言实现可以有不同的选择：

• 数组或表，如vector、list，此时允许平行边或重边和自环边，查询时间为O(V)，插入时间为O(1)
• 树，tree（stl set），不允许平行边，查询时间和插入时间都为O(logV)
• 散列表，hashtable，无序，不允许平行边，插入查询时间为O(1)

图支配理论

支配集：设$S$是图$G$的结点组成的集合，如果G的每一个结点要么在S中要么与S中的结点相邻，则S是G的支配集

最小支配集：如果支配集S的任意真子集都不是支配集，则称S为极小支配集，元素数目最小的支配集叫做最小支配集

独立支配集：支配集S中的结点互不相邻

应用：任务指派，校车路线安排，通讯网络，无线电台布局，社群网络理论和地面测量

知识内容	具体算法	应用	经典问题
图基本概念与算法	图的表示、图的遍历（广度+深度）、图的环或圈检测、拓扑排序算法	构成图论的基本内容，存储，基本遍历搜索与拓扑排序	遍历搜索，处理有前后关联的任务安排
距离与连通性	最短路径算法、 图连通性判断算法	路径规划、统筹规划与系统可靠性检验	路径规划，设施布局，网络可靠性检测
图着色	解决涂色问题（Welch-Powell算法）	解决资源有限和其他约束条件下的分配问题	课程表问题，安全装箱问题，地图着色问题，信道分配问题
可平面性	判断是否为平面图（DMP算法，平面嵌入的灌木生长算法，PFA,st编码算法）	一个图可以画成任意两条边都不相交的样子，多用于工程规划领域	印制电路板，道路布局
欧拉图与哈密顿图	求解欧拉回路（Hierholzer、Fleury、DFS搜索）、判别欧拉回路，求解哈密顿圈问题	是否/如何遍历所有路径/节点并避免重复	中国邮递员问题，七桥问题
有向图与网络	最大流算法(2F算法，分层算法，Edmond-Karp 算法)，极大流算法，有上下界网络最大流算法，有供需要求的网络流算法	优化调度分配	交通网络调度
树与二分图	最小生成树(DFS+BFS),最优树算法(Kruskal算法)、有序二元树	几乎所有图论都离不开树	Huffman编码；最佳追捕问题
匹配理论	匈牙利算法、求最佳匹配的有效算法、KM算法	在匹配与许配问题中进行最优化处理	BernoulliEuler错插信笺问题；Hall婚配定理；应聘问题
图支配问题	支配树构造(Lengauer Tarjan 算法)	对影响与覆盖问题的数学抽象	皇后问题，中心台站选址

隐私需求

隐私分析

• 数据隐私需求
• 图论相关的运算需求

参与图论运算的数据有

• 结点（集合）
• 路径（集合）
• 权重值（集合）
• 图形组合

图论相关运算

• 最短路径？/最小花费？
• 路径规划？
• 事物安排？
• 优化调度/资源分配？
• 最大流量？

路径相关的隐私计算需求 交易图谱相关的隐私计算需求 社会关系网相关的隐私计算需求

知识内容	具体算法	应用	经典问题	隐私计算需求
图基本概念与算法	图的表示、图的遍历（广度+深度）、图的环或圈检测、拓扑排序算法	构成图论的基本内容，存储，基本遍历搜索与拓扑排序	遍历搜索，处理有前后关联的任务安排	在隐私环境下的遍历搜索
距离与连通性	最短路径算法、 图连通性判断算法	路径规划、统筹规划与系统可靠性检验	路径规划，设施布局，网络可靠性检测，人际关系连接	在隐私背景下的最短路径选择与连通性判定
图着色	解决涂色问题（Welch-Powell算法）	解决资源有限和其他约束条件下的分配问题	课程表问题，安全装箱问题，地图着色问题，信道分配问题	在隐私背景下的资源最优化安排
可平面性	判断是否为平面图（DMP算法，平面嵌入的灌木生长算法，PFA,st编码算法）	一个图可以画成任意两条边都不相交的样子，多用于工程规划领域	印制电路板，道路布局	例如电路板布局，在交付设计图时保护信息
欧拉图与哈密顿图	求解欧拉回路（Hierholzer、Fleury、DFS搜索）、判别欧拉回路，求解哈密顿圈问题	是否/如何遍历所有路径/节点并避免重复	中国邮递员问题，七桥问题	在隐私环境下的特殊遍历
有向图与网络	最大流算法(2F算法，分层算法，Edmond-Karp 算法)，极大流算法，有上下界网络最大流算法，有供需要求的网络流算法	优化调度分配	交通网络调度	例如隐私匿名交易过程中的优化调度
树与二分图	最小生成树(DFS+BFS),最优树算法(Kruskal算法)、有序二元树	几乎所有图论都离不开树	铁路网规划，Huffman编码；最佳追捕问题	在隐私背景下的最小生成树问题
匹配理论	匈牙利算法、求最佳匹配的有效算法、KM算法	在匹配与许配问题中进行最优化处理	BernoulliEuler错插信笺问题；Hall婚配定理；应聘问题	隐私背景下的匹配问题
图支配问题	支配树构造(Lengauer Tarjan 算法)	对影响与覆盖问题的数学抽象	皇后问题，中心台站选址	在隐私背景下的影响与覆盖问题

参考文献

主要参考：

书籍

《图论》–王树禾

《A friendly introduction to graph theory》（《图论简明教程》）

博客：

https://blog.51cto.com/nxlhero/1213947

http://www.srcmini.com/1635.html

https://oi-wiki.org/graph/euler/

https://juejin.cn/post/6924668410416791566

https://zhuanlan.zhihu.com/p/34442520

https://zhuanlan.zhihu.com/p/77766801

https://zhuanlan.zhihu.com/p/76544669

https://www.docin.com/p-436994535.html

https://www.cnblogs.com/dragonir/p/6011561.html

…