【深度学习理论】(3) 激活函数
各位同学好,最近学习了CS231N斯坦福计算机视觉公开课,讲的太精彩了,和大家分享一下。
激活函数的作用是把神经元的输入线性求和后,放入非线性的激活函数中激活,正因为有非线性的激活函数,神经网络才能拟合非线性的决策边界,解决非线性的分类和回归问题
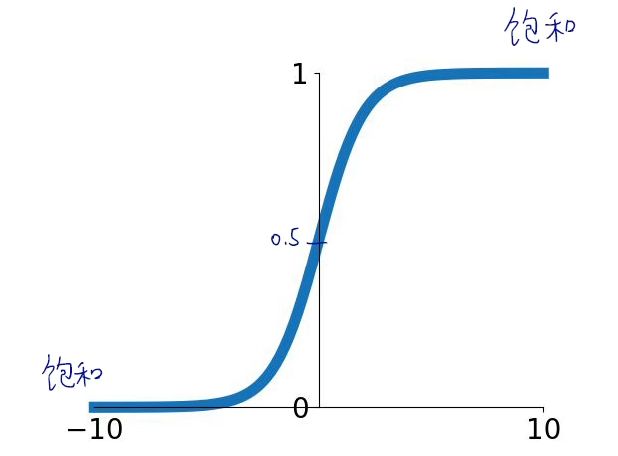
1. Sigmoid 函数
作用:将负无穷到正无穷的输入,映射到0到1之间。
公式:![]()
若x=0,函数值=0.5,;若x很大时,函数值非常接近1;若x很小时,函数值非常接近0
特点:
(1)将负无穷到正无穷的任何输入,都挤压成0到1之间的一个数,又称为挤压函数
(2)可解释性好,可类比神经细胞是否激活。函数输出的是0到1之间的值,相当于一个二分类问题,0是一个类别,1是另一个类别
缺陷:
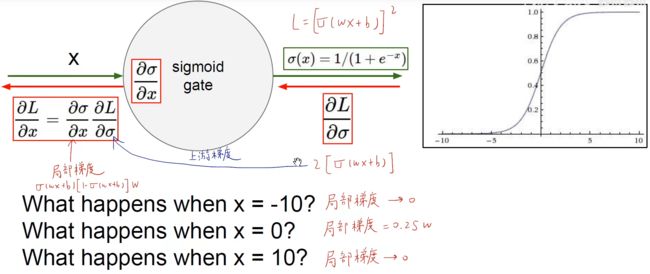
(1)饱和性导致梯度消失。x过小或过大时,梯度接近0。
(2)函数输出值都是正数,不是关于零对称的。
如下图,如果两个隐含层的输出都是正数,会导致每个神经元中所有对权重的偏导数都是同号的。也就是说,对于一个神经元所有的权重,要么同时增大,要么同时减小。
假如函数是 ![]() 用 sigmoid 函数激活,对内层函数求偏导,
用 sigmoid 函数激活,对内层函数求偏导,![]() 。这个xi是神经元的输入,也是上个神经元的输出。若上个神经元用sigmoid函数激活,那么xi肯定是一个正数。
。这个xi是神经元的输入,也是上个神经元的输出。若上个神经元用sigmoid函数激活,那么xi肯定是一个正数。
也就是,对于函数的 w1, w2, w3 来说,各自的偏导数都是正数,即所有的权重是一同增大和减小的。如下面的右图所示,横轴代表w1的偏导数,纵轴代表w2的偏导数。权重的更新方向始终是第一象限或第三象限,要么都是正的要么都是负的。如下图中蓝色线条,现在需要让w1增大(正),让w2减小(负),是没办法一步到位的。需要大家先一起减小,再一起增大,来回滑动,生成锯齿形优化路径。
(3)指数运算较消耗资源。相比加减乘除之类的运算,是比较消耗资源的。
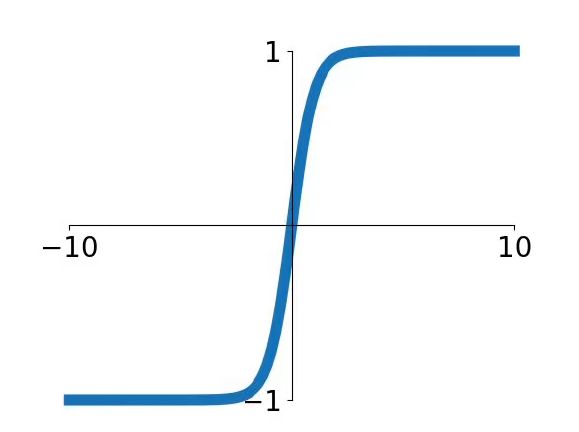
2. tanh 函数
双曲正切函数和 sigmoid 函数类似,两者之间可通过缩放和平移变换相互转换。
特点:
(1)饱和性导致梯度消失
(2)将负无穷到正无穷的任何输入,都挤压成-1到1之间的一个数
(3)函数输出值有正有负,关于0对称
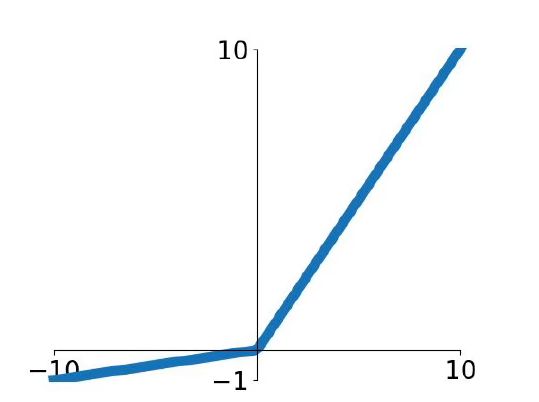
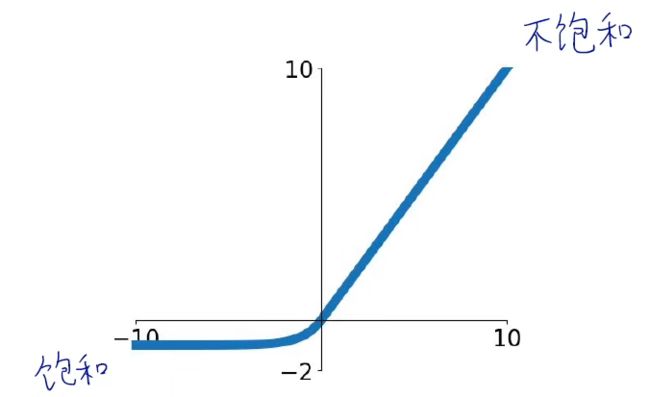
3. ReLU 函数
ReLU函数又称为修正线性单元,将输入小于0的数都抹为0。
公式:![]()
特点:
(1)函数不会饱和,x大于0时,输入有多大,输出就有多大。
(2)计算简单,几乎不消耗计算资源。
(3)x大于0时,梯度能得到保留,因此ReLU函数比sigmoid函数的收敛速度快6倍以上。
缺陷:
(1)输出不是关于0对称
(2)x小于0时,梯度为0。导致一些神经元是死的(dead ReLU),既不会产生正的输出,也不会产生正的梯度,也不会发生更新。
导致Dead ReLU原因是:① 初始化不良,随机初始化的权重,让神经元所有的输出都是0,梯度等于0;② 学习率太大,步子跨太大容易乱窜
为了解决Dead ReLU的问题,在ReLU的权重上加一个偏置项0.01,保证所有的神经元一开始都能输出一个正数,使所有的神经元都能获得梯度更新
4. ReLU 函数改进
为了解决ReLU函数x小于0,梯度为0的情况,推出了Leaky ReLU 和 ELU函数。
Leaky ReLU函数给x小于0时,乘以一个非常小的权重。
公式:![]()
x小于0时满足线性关系
ELU函数给x小于0时,使用指数函数
改善了ReLU函数输出不关于0对称的问题,但是使用指数运算会带来更大的计算量
5. Maxout
如下图,现在有两个输出神经元,现在使用另外一套神经网络对这两个输出做处理,使用5个神经元(5套权重)对输出进行处理,从这5个输出结果中选出最大的最为激活函数输出。
特点:不仅仅是一种激活函数,还改变了网络的结构,因为引入了新的神经元,而且参数个数呈k倍增加
6. 总结
(1)使用ReLU函数,要注意学习率不能太大,否则会导致梯度消失
(2)可以使用Leaky ReLU或ELU或Maxout,代替ReLU
(3)不要在中间层使用Sigmoid函数。如果是二分类问题,可以输出层使用sigmoid函数
(4)可以使用tanh函数,但不要对它抱有太大的希望。