线索二叉树构建和遍历
线索二叉树
文章目录
- 线索二叉树
-
- 引出线索
- 解决方案(以中序线索树为例)
-
- 引论:
- 策略:
- 问题1:
-
- ♥ 对策
- 线索二叉树的节点类型定义
- 线索化二叉树
-
-
- ♥ 线索化算法
- ♥ 建立中序线索二叉树的算法
- ♥ 算法实现
-
- 遍历线索化二叉树
-
- 引言:
-
- ♥ 遍历思路(中序遍历举例):
- ♥ 实操遍历:
- ♥ 实操框架
- ♥ 代码实操
引出线索
什么是线索呢?
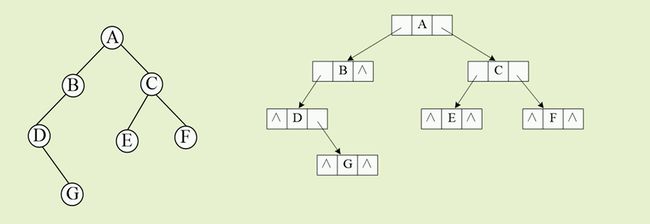
我们想把上面的左图的二叉树转换成右图的二叉树,就需要构造链式二叉树了,但是我们会发现,我们的链节点每个节点会有很多空指针, 我们能浪费这些空间吗? 这些空间还能被我们利用吗?

我们的任务就是构造二叉树,然后去遍历它,我们采用的是递归的方法构造,遍历的时候也是采取递归的算法遍历,这样很容易理解,但是同时我们也会发现–递归有的时候会拖慢进程,明明我这个节点在此处有空余指针可以存储下一个节点的信息,为什么不能利用起来呢? 这就引出了我们的下面的线索二叉树.
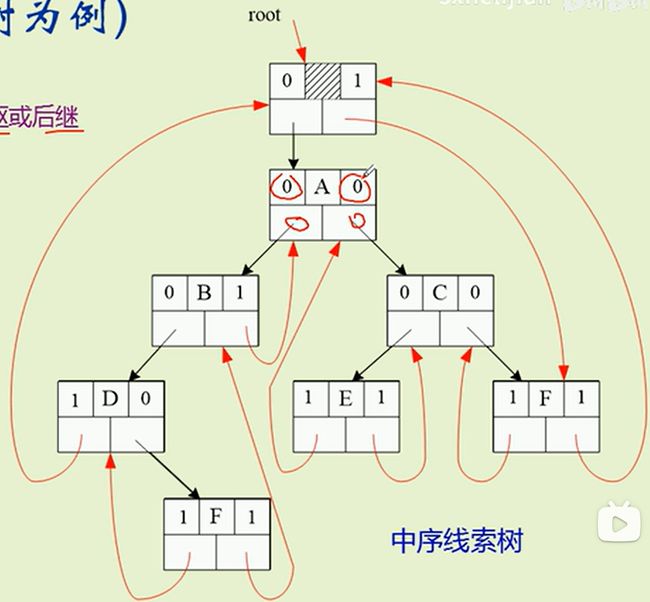
解决方案(以中序线索树为例)
引论:
我们知道遍历操作是非常常用的操作, 而在遍历操作中,我们接触过递归算法,非递归算法,很麻烦,操作很多的进行逐层遍历。此时我们就发现了空指针的浪费现象,我们能不能利用空闲的指针,去表示某种遍历的顺序。当我们给节点赋予某种遍历的特性,我们在遍历的时候就会非常方便了。我们就不用等递归返回到上一层,直接指向上一层要访问的节点即可。大大减轻了程序运行的复杂程度。
策略:
•用空指针域按遍历顺序指向节点的前驱或后继。

首先我们看到的是每个链式节点都有左右指针,但是左右指针有的有孩子,有的没有孩子,所以我们就需要给节点的每个指针域进行标志,然后再赋予相应的指针。对于如何串联起来这颗二叉树呢?当然需要头指针了,我们来一个空的头指针进行标识,然后串联第一个遍历的节点和最后一个访问的节点。
每个节点,如果其左指针为空,则指向其前一个节点,其前一个节点的后继指针如果为空,则指向遍历的其后一个节点。
问题1:
• 我们上面的思路和构图都有了, 下面我们开始构造了,但是如果去区别节点的指针指向是孩子,还是作为线索呢?
♥ 对策
我们可以对节点的数据结构进行重新构造,我们可以通过遍历的方式,来确定节点的左右指针是否为空。在遍历的过程中,就可以对其进行对应的赋值构造。

线索二叉树的节点类型定义
typedef struct node
{
ElemType data; //定义数据域
int ltag,rtag; //定义左右孩子的标志位,1为线索,0为有孩子
struct node *lchild; //左指针
struct node *rchild; //右指针
}TBTNode;
线索化二叉树
所谓线索化二叉树, 就是要通过遍历,将原来需要递归遍历的二叉树,变成能够利用指针快捷访问节点的过程.
我们上面已经构造了线索二叉树的节点,接下来,就是通过按照递归遍历(中序遍历为例)的方式,遍历一遍二叉树,这样我们就知道每个节点的对应信息是多少了,从而进行构建线索二叉树.
♥ 线索化算法
▪ 遍历二叉树,在遍历的过程中,检查当前节点的左、右指针域是否为空。如果为空,将它们改为指向前驱节点或后继节点的线索。
▪ 创建一个头结点,并建立头节点与二叉树的根节点的线索;最后,建立最后一个节点与头结点之间的线索。
♥ 建立中序线索二叉树的算法
▪ CreaThread(b)算法: 是将以二叉链存储的二叉树b进行中序线索化,并返回线索化后头结点的指针root.
把构造好的线索二叉树, 用一个头结点链接起来 , 方便我们进行标识和传输
•Thread( p)算法:用于以*p为根节点的二叉树中序线索化.*
算法构造分析:
我们要实现一个二叉树的线索化, 就需要先去遍历(先序遍历)一遍,这样才能知道按照顺序遍历到的节点是否有空指针或者孩子.
既然要遍历,那当然是先序递归遍历,回顾一下先序遍历的过程,我们每次处理的都是同一个层次, 至于其他层, 通过递归都会依次实现,所以我们只需要把同一层遇到的所有情况处理完, 那等到递归调用子树的时候, 也会把子树当成一个树,去处理同样的情况.
我们在遍历的时候,也不要忘记我们的任务, 我们是要处理利用每个节点空指针:
左指针为空,则指向前驱节点
右指针为空,则指向后继节点
♥ 算法实现
• Thread( p)算法:用于以*p为根节点的二叉树中序线索化.*
//表示要线索化的p的前驱节点
TBTNode *pre; //刚开始, p是二叉树的根, pre是线索二叉树的头结点
//传入要线索化的二叉树的根指针地址
void Thread(TBNode *&p) //注意细节,这里传入的是"*&"---指针地址
{
//不为空,就继续线索化
if(p!=NULL)
{
//我们需要在同一个层级上进行线索化
//先传入的是二叉树的根, 按照先序遍历的次序,我们要把其左子树线索化
//线索化的方式就是,传入左孩子,递归方法会一直找到没有左孩子的结点
//我们通过此调用, 就相当于把几个层次都入栈了,等待返回的时候,我们就构造好了左子树
Thread(p->lchild);
//此时当我们找到第一个遍历节点的时候,就会跳出,然后进行下一步操作
//此时我们已经找到了"D"
//接下来的操作就是 把"D"线索化,此时我们有什么呢? 前驱节点root和 *p所指向的"D"
//我们下面就处理这个节点,先把D 和 前驱节点 root 联系起来
if(p->lchild==NULL)
{
p->lchild==pre; //如果*p没左孩子,那就把左指针指向前驱节点pre
p->ltag=1; //同时左节点标记为1
}
else //否则就是有左孩子
{
p->ltag=0; //左指针标记置为0
}
//现在p的左指针处理完了, 那p 的右指针还处理吗? 后续再处理,我们需要先处理p的前驱节点pre
//看pre是否有右孩子,没有的话,指向其后继节点 *p即可,充分利用指针
if(pre->rchild==NULL)
{
pre->rchild=p;
pre->rtag=1;
}
else
{
pre->rtag=0; //否则有右孩子,说明右指针有用,不能当线索,标志置为0
}
//截止到目前,我们处理了 前驱节点的pre的右指针和 pre的后继节点 p的左指针
//下面就是处理p的右指针和接下来的节点了
//我们把*p当做pre, 接着遍历处理下面的节点
pre = p;
//现在在同一个层级内,我们已经处理完左子树,下面该右子树了
Thread(p->rchild);
}
}
//---------------------------------------------------------------------------------
//此时我们就完成了对二叉树遍历过程中的,逐个节点的线索化
//注意 pre 和 p 之间的交替关系
▪ CreaThread( b)算法: 是将以二叉链存储的二叉树b进行中序线索化,并返回线索化后头结点的指针root.*

//现在我们的二叉树节点已经大致线索化完成了,剩下的就是头结点链接起来了
//传入要线索化的二叉树
TBTNode *CreaThread(TBTNode *b)
{
//定义线索二叉树的根节点root根节点
TBTNode *root;
//为头结点分配空间
root = (TBTNode *)malloc(sizeof(TBTNode));
//我们的头结点,我们肯定知道其标志位
root->ltag=0; //如果二叉树不为空,那么头节点root左孩子指向树根,起到如图的链接作用
root->rtag=1; //为了把线索二叉树构成环,所以需要当做线索
root->rchild=b; // 刚开始,只遍历到树根,所以root的右指针指向b
if(b==NULL) //当传入的树为空时,就把头结点左指针指向头结点本身
{
root->lchild=root;
}
else //传入结点不为空时,我们就把头结点和二叉树链表链接起来
{
root->lchild=b; //左指针指向二叉树的根
pre = root; //头结点当做前驱节点pre
Thread(b); //前驱节点有了,就可以构造了,调用构造线索二叉树
pre->rchild=root; //返回的时候,说明已经构造完了,开始把最后一个节点的右指针指向root
pre->rtag=1; //最后一个节点的右指针标志为1
root->rchild=pre; //根节点root 的右指针指向pre
}
return root;
}
遍历线索化二叉树
引言:
遍历二叉树当然用递归最方便, 但是之前我们已经说了递归遍历的效率问题, 所以我们现在引出线索化二叉树的意义就是方便我们进行遍历.所以构造线索化二叉树遍历算法,我们最好把流程走一遍,观察规律, 然后具体情况,具体对待的遍历,使用循环的话,的确会丧失一些代码的可读性,但为了效率问题,我们还是观察规律, 按照递归的思想,然后借助构造的线索,进行有序高效遍历。

♥ 遍历思路(中序遍历举例):
我们现在已经构造好了线索, 一旦检测到节点的右指针标志为1 ,我们就不用再用递归返回按层次遍历了, 把遍历的指针直接指向其右孩子指针即可.
至于具体如何去构造一个层次 ,需要我们具体去走一遍.
♥ 实操遍历:
① 我们先传入根节点, 然后我们把遍历的指针指向根节点的右孩子, 因为其右孩子就是我们构造的线索二叉树的根
② 线索二叉树的遍历现在就是一条线,此时我们拿到根节点, 当然不能直接遍历,而是根据中序遍历的顺序,需要先找到左子树中没有左孩子的节点,然后将其输出即可(这是此层级输出的第一个节点)。
③ 根据根-左-右顺序,②中输出的就是根,因为“D”没有左节点了,在此层级内,下面该输出右节点“F”了。
④ 此时还未结束,我们要把F当做下一层级的根节点,然后输出, 此时我们会发现,我们的 “F” 中有我们的线索(rtag==1 && *p没有遍历到头结点) , 所以我们就可以利用线索,直接将 p 赋值成
p->rchild, 然后此时我们相当于递归思想内,直接省去了return ,直接跳到上一层级的根节点了,所以我们直接输出 p->data 即可 , 就这样一直循环跳跃,如果(rtag==1 && *p没有遍历到头结点)就一直输出即可, 但是早晚左子树会处理完, 我们会到A , 此时根节点A没有线索了,我们只能跳出循环了.
⑤ 接下来我们要处理的情况就是,当节点的 rchild 指向的不是线索的话, 我们就跳出循环了,不是线索的话,此时我们此层级的根当然访问完了, 左子树按照递归的顺序也访问完了, 就剩下右子树了,所以直接访问右子树就行了,知道访问到 p == 头结点 为止。
⑥ 我们的总体思想: 还是在递归遍历同一层级的基础上,面对不同情况,所作出的判断和处理,保证循环能够利用线索指针执行我们上图所示的遍历思想。
♥ 实操框架
遍历函数(传入线索二叉树)
{
遍历指针指向头结点的左孩子;
while(遍历指针没遍历到头结点就一直遍历)
{
先找到左子树的左下孩子;
然后输出数据域;
//在此层级内,我们已经输出根节点,没有左孩子了,所以要判断其是否有线索
while(右指针标志为1 && 右指针不指向头结点) //遍历不结束并且有线索
{
//符合我们就利用线索,进行输出上一层级的根节点(因为此层级已经处理完了)
指针p指向线索指针;
输出上一层级的根*p;
}
//跳出的时候,我们已经遍历到了二叉树的根节点A,此时A右指针没有线索
//此时根已经输出,所以就遍历输出其右子树
指针指向右子树;
}
}
♥ 代码实操
void ThlnOrder(TBTNode *b)
{
TBTNode *p = tb->lchild;
while(p!=tb)
{
while(p->ltag==0)
{
p = p->lchild;
}
printf("%c",p->data);
while(p->rtag == 1 && p->rchild != tb)
{
p = p->rchlid;
printf("%c",p->data);
}
p = p->rchild;
}
}
