线索二叉树中序非递归线索化以及递归线索化构建和遍历算法

引文

大部分教材给出了 线索二叉树的中序递归线索化以及中序遍历，但是没给出非递归，现在网上大部分非递归算法代码各种条件判断写的比较离谱，所以干脆自己总结了一个清晰的。线索二叉树中序非递归线索化以及递归线索化构建和遍历算法

前置

构建线索二叉树结构体,这里我为了方便，将普通二叉树结构体和线索二叉树结构体混杂在一起，只是名字变了，方便共同使用栈或者是队列的代码。

还需要构建栈，不懂栈的朋友们请百度。

#include 
#include 
#define MaxSize 50
typedef int ElemType;
//链式存储二叉树
typedef struct BiTNode{
    ElemType  data;
    struct BiTNode *lchild,* rchild;
    int ltag,rtag;
} BiTNode,*BiTree,ThreadNode,*ThreadTree;

//------------------栈开始------------
//是用顺序栈
typedef struct{
    BiTree data[MaxSize];
    int top;
} SqStack;
//初始化
void initSqStack(SqStack &Stack){
    Stack.top = -1;
}
bool isEmpty(SqStack &Stack){
    return Stack.top==-1;
}

//入栈
bool push(SqStack &Stack,BiTree& T){
    if(Stack.top==MaxSize-1){
        return false;
    }
    Stack.data[++Stack.top] = T;
    return true;
}

//出栈
bool pop(SqStack &Stack,BiTree& T){
    if(Stack.top==-1){
        return false;
    }
    T = Stack.data[Stack.top--];
    return true;
}
//获取栈顶元素
bool getStackTop(SqStack &Stack,BiTree &T){
    if(Stack.top==-1){
        return false;
    }
    T = Stack.data[Stack.top];
    return true;
}

//---------------栈结束---------------

//给一个二叉树以层序遍历的方式插入结点
void addNode(BiTree &T,ElemType value){

    BiTree innerTree = NULL;
    BiTNode *node = (BiTNode *) malloc(sizeof(BiTNode));
    node->data = value;
    node->lchild = NULL;
    node->rchild = NULL;
    node->rtag = 0;
    node->ltag = 0;
    if(T==NULL){
        T = node;
        return;
    }
    SqQueue Q;
    initQueue(Q);
    enQueue(Q,T);
    while (deQueue(Q,innerTree)){
        if(innerTree->lchild!=NULL){
            enQueue(Q,innerTree->lchild);
        } else{
            innerTree->lchild = node;
            break;
        }
        if(innerTree->rchild!=NULL){
            enQueue(Q,innerTree->rchild);
        } else{
            innerTree->rchild = node;
            break;
        }
    }
}


BiTree initBiTree(ElemType value[],int n){
    BiTree T =NULL;
    for (int i=0;i

上面就是 需要准备好的一些代码。
我们通过 getBiTree()方法直接调用就能获得一颗二叉树，但是这个二叉树是非线索化的，因此，我们需要将它进行线索化。

线索二叉树中序递归线索化构建

二叉树的线索化是将二叉链表中的空指针改为指向前驱或后继的线索。而前驱或后继的信息只有在遍历时才能得到，因此线索化的实质就是遍历一次二叉树。
以中序线索二叉树的建立为例。附设指针 pre 指向刚刚访问过的结点，指针p 指向正在访问的结点，即pre指向p 的前驱。在中序遍历的过程中，检查p的左指针是否为空，若为空就将它指向pre;检查pre的右指针是否为空，若为空就将它指向p。

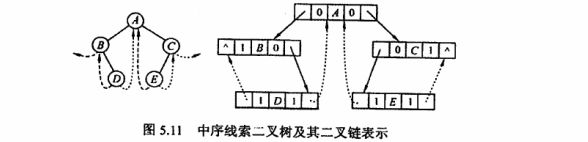
这里我们是基于二叉树的中序遍历思想来写代码，但是需要考虑到的点是，pre和p在 访问结点的时候应该做的事情和普通的中序遍历不一样罢了。
找一个中间态，此时pre指向D,p指向A。
我们此时的操作，

1. 我们肯定想将p的lchild指向D，但是很明显这里的p->lchild！=NULL，有左孩纸了，所以，肯定要有判断条件 p->lchild!=NULL才能进行线索化构建。让 p->lchild=pre 然后 p->ltag = 1
2. 我们肯定想将pre的rchild指向p，但是肯定要有判断条件，因此pre!=NULL&&pre->rchild==NULL的时候，才能进行线索构建。
   不然pre=NULL直接空指针。
   3.上面两个操作之后，那么肯定要变化 p 和pre 的位置，让pre = p。
   基于这个中间态明确边界条件，首先是基于中序遍历递归算法写的，那么，条件肯定是p!=NULL进入递归状态。然后就是一样的操作了。

//中序线索化
//递归
void inThread(ThreadTree& p,ThreadTree& pre){
    if(p!=NULL){
        inThread(p->lchild,pre);
        if(p->lchild==NULL){
            p->lchild = pre;
            p->ltag = 1;
        }
        if(pre!=NULL&&pre->rchild==NULL){
            pre->rchild = p;
            pre->rtag = 1;
        }
        pre = p;
        inThread(p->rchild,pre);
    }
}

到这里，整个递归执行完成后，pre肯定指向的是中序遍历的最后一个结点(可以自己完成推演一遍)，我们只需要对这个最后一个结点进行一次线索化就ok了。
因此有了

//线索化主函数
void CreateInThread(ThreadTree T){
    ThreadNode  * pre = NULL;
    if(T!=NULL){
        inThread(T,pre);
        pre->rchild=NULL;
        pre->rtag = 1;
    }
}

线索二叉树非递归算法线索化构建

一样利用中序遍历非递归算法来完成这个操作。明确下面这个思想。先找到中间态，再找到边界条件。

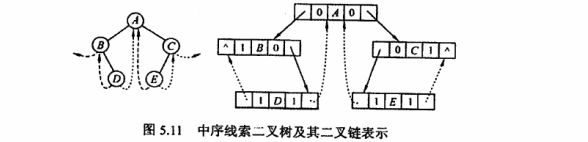
1. 我们肯定想将p的lchild指向D，但是很明显这里的p->lchild！=NULL，有左孩纸了，所以，肯定要有判断条件 p->lchild!=NULL才能进行线索化构建。让 p->lchild=pre 然后 p->ltag = 1
2. 我们肯定想将pre的rchild指向p，但是肯定要有判断条件，因此pre!=NULL&&pre->rchild==NULL的时候，才能进行线索构建。
   不然pre=NULL直接空指针。
   3.上面两个操作之后，那么肯定要变化 p 和pre 的位置，让pre = p。
   基于这个中间态明确边界条件，首先是基于中序遍历递归算法写的，那么，条件肯定是p!=NULL进入递归状态。然后就是一样的操作了。

然后基于中序遍历非递归算法的框架(如果这个不是很清楚可以移步我的另一篇 博客，点击这里)，
整个中序非递归都是基于
while(p!=NULL||栈非空)来进行,凡是二叉树非递归前中后，都用栈(有些诡异的算法可以不用)，但是考试用来方便。如果这里不懂，必须要看懂 中序遍历非递归，不然不会的还是不会。

//线索二叉树 非递归算法线索化
void creatThread2(ThreadTree &T){
    ThreadNode  * p = T,*pre = NULL;
    SqStack stack;
    initSqStack(stack);
    //利用 之前中序遍历非递归算法特性 完成 对线索二叉树 非递归算法构建
    //利用 pre保存 中序遍历序列的前驱结点
    while (p!=NULL||!isEmpty(stack)){
        if(p!=NULL){
            push(stack,p);
            p= p->lchild;
        }else{
            pop(stack,p);
            if(p->lchild==NULL){
                p->lchild = pre;
                p->ltag = 1;
            }
            if(pre!=NULL&&pre->rchild==NULL){
                pre->rchild = p;
                pre->rtag = 1;
            }
            pre= p;
            p = p->rchild;
        }
    }
    //处理最后一个结点
    pre->rchild = NULL;
    pre->rtag = 1;
}

中序线索二叉树遍历

遍历分为三个子步骤

1. 将p指向找到的第一个结点,访问
2. 找到p结点的后继结点
3. 将p指向p的后继，重复1
   这样，我们要拆除来两个方法
   1是找到当前结点作为树的第一个中序遍历结点。这个方式非常简单，中序遍历是左根右，只要我们一直 遍历 p = p->lchild，刷到p->ltag=1的时候，就代表了这个p就是第一个中序遍历的结点了。 这样看来，其实 对中序遍历来说，凡是 树的最左下的结点(不一定是叶结点)，就是这第一个结点。
   2.是找到p结点的后继，一般来说是如果p的rtag =1的话，那么后继就是 p ->rchild了，但是奈何，万一 p的rtag=0，相当于说 p的右本身就有孩纸，这个孩纸我们一样将其看做一颗子树(毕竟你不知道这个孩纸还有木有孩纸)，那么 p的右边连了一颗子树，我要找的p的中序后继，实际上就是变成了 找 p的右边这颗子树中序遍历的第一个结点。
   然后我们以p的右孩纸作为根结点，调用一次1步骤写的方法，就得到了这颗子树的第一个中序遍历结点。直接访问就完事了
   因此可以写出下面的遍历算法:

//中序线索二叉树的 遍历
//中序遍历
ThreadNode * FirstNode(ThreadNode * p){
    while(p->ltag==0){
        p = p ->lchild;
    }
    return  p;
}
ThreadNode * NextNode(ThreadNode * p){
    if(p->rtag==0){
        return FirstNode(p->rchild);
    } else{
        return p->rchild;
    }
}

void inThreadOrder(ThreadNode  * T){
    for (ThreadNode * p = FirstNode(T);p!=NULL;p = NextNode(p)) {
        printf("%d ",p->data);
    }
}

启动

用了那么多，我们main方法走一波

int main(){
    BiTree T = getBiTree();
	 //中序线索化 递归
    //CreateInThread(T);
    //中序线索化 非递归
    creatThread2(T);
    //中序遍历线索二叉
    inThreadOrder(T);
}