如何利用k-means算法对图片颜色进行聚类并实现图像压缩？（附Python代码+数据集）

整理不易，希望各位看官大大随手点个赞，各位的鼓励是我不竭的学习动力。

在进行学习之前，我们需要先了解一个知识点：

RGB图像，每个像素点值范围为[0-255]

我们需要用到的数据集下载通道：

链接：https://pan.baidu.com/s/10EGibyqZKnIph-CHSnwx9Q
提取码：6666

利用k-means算法对图片颜色进行聚类

1.首先我们导入我们可能用到的包：

import matplotlib.pyplot as plt
from scipy.io import loadmat
from numpy import *
from IPython.display import Image

2.接下来我们导入相应的RGB图像：

def load_picture():
    path='./data/bird_small.png'
    image=plt.imread(path)
    plt.imshow(image)
    plt.show()

我们看一下图片：

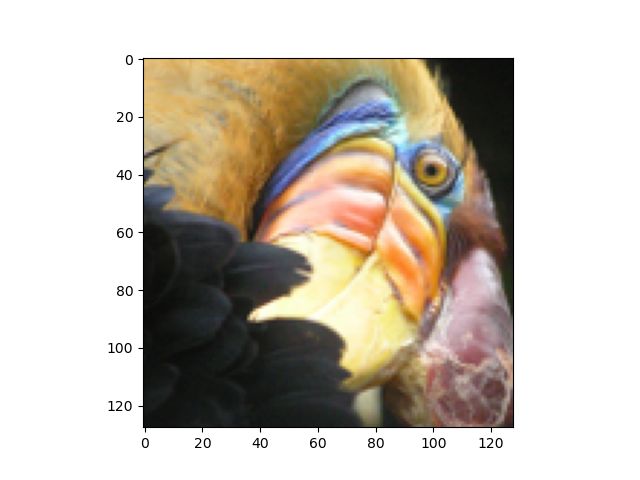
注意：在这里我们可能会遇到另一种导入的方法：

from IPython.display import display,Image
path='./data/bird_small.png'
display(Image(path))

但是值得一提的是，上面的方法在jupyter中可以正常实现，但是在Pycharm中是无法打开的，得到的结果为：

<IPython.core.display.Image object>

这里不再赘述，具体的可以去看我之前的博客文章：

https://blog.csdn.net/wzk4869/article/details/126047821?spm=1001.2014.3001.5501

3.我们导入对应的数据集：

def load_data():
    path='./data/bird_small.mat'
    data=loadmat(path)
    return data

这里的数据集依旧是导入的mat格式，读取方式和转换方法在之前的博客中已经讲解：

https://blog.csdn.net/wzk4869/article/details/126018725?spm=1001.2014.3001.5501

我们展示一下数据集：

data=load_data()
print(data.keys())
A=data['A']
print(A.shape)

dict_keys(['__header__', '__version__', '__globals__', 'A'])
(128, 128, 3)

是一个三维数组。

4.数据的归一化：

这一步是相当有必要的，如果不进行，会报错，具体的结果见我之前的博客文章：

https://blog.csdn.net/wzk4869/article/details/126060428?spm=1001.2014.3001.5501

我们归一化的实现流程如下：

def normalizing(A):
    A=A/255.
    A_new=reshape(A,(-1,3))
    return A_new

至于归一化为什么选择除以255，不是减去均值除以标准差，原因也在下面的文章中讲解。

https://blog.csdn.net/wzk4869/article/details/126060428?spm=1001.2014.3001.5501

我们看一下归一化后的数据集：

[[0.85882353 0.70588235 0.40392157]
 [0.90196078 0.7254902  0.45490196]
 [0.88627451 0.72941176 0.43137255]
 ...
 [0.25490196 0.16862745 0.15294118]
 [0.22745098 0.14509804 0.14901961]
 [0.20392157 0.15294118 0.13333333]]
 
(16384, 3)

这里可以很明显的看到，数据集均变为了0-1之间，并且把三维数组转换成了二维数组。

A_new=reshape(A,(-1,3))这一步对于一部分小伙伴可能会感到吃力，不过没关系，我在之前的博客中也有总结类似的reshape函数的用法，这里不再赘述：

https://blog.csdn.net/wzk4869/article/details/126059912?spm=1001.2014.3001.5501

至此，我们数据集的处理过程已经结束，我们给出k-means算法，过程与之前相同。

5.k-means算法的实现

def get_near_cluster_centroids(X,centroids):
    m = X.shape[0] #数据的行数
    k = centroids.shape[0] #聚类中心的行数，即个数
    idx = zeros(m) # 一维向量idx，大小为数据集中的点的个数，用于保存每一个X的数据点最小距离点的是哪个聚类中心
    for i in range(m):
        min_distance = 1000000
        for j in range(k):
            distance = sum((X[i, :] - centroids[j, :]) ** 2) # 计算数据点到聚类中心距离代价的公式，X中每个点都要和每个聚类中心计算
            if distance < min_distance:
                min_distance = distance
                idx[i] = j # idx中索引为i，表示第i个X数据集中的数据点距离最近的聚类中心的索引
    return idx # 返回的是X数据集中每个数据点距离最近的聚类中心

def compute_centroids(X, idx, k):
    m, n = X.shape
    centroids = zeros((k, n)) # 初始化为k行n列的二维数组，值均为0，k为聚类中心个数，n为数据列数
    for i in range(k):
        indices = where(idx == i) # 输出的是索引位置
        centroids[i, :] = (sum(X[indices, :], axis=1) / len(indices[0])).ravel()
    return centroids

def k_means(A_1,initial_centroids,max_iters):
    m,n=A_1.shape
    k = initial_centroids.shape[0]
    idx = zeros(m)
    centroids = initial_centroids
    for i in range(max_iters):
        idx = get_near_cluster_centroids(A_1, centroids)
        centroids = compute_centroids(A_1, idx, k)
    return idx, centroids

def init_centroids(X, k):
    m, n = X.shape
    init_centroids = zeros((k, n))
    idx = random.randint(0, m, k)
    for i in range(k):
        init_centroids[i, :] = X[idx[i], :]
    return init_centroids

6.绘制压缩后的图像：

def reduce_picture():
    initial_centroids = init_centroids(A_new, 16)
    idx, centroids = k_means(A_new, initial_centroids, 10)
    idx_1 = get_near_cluster_centroids(A_new, centroids)
    A_recovered = centroids[idx_1.astype(int), :]
    A_recovered_1 = reshape(A_recovered, (A.shape[0], A.shape[1], A.shape[2]))
    plt.imshow(A_recovered_1)
    plt.show()

我们结果为：

总结：虽然前后图像不尽相同，但是我们经过聚类后的图像明显保留了原图片的大部分特征，并且减少了内存空间。

源代码

import matplotlib.pyplot as plt
from scipy.io import loadmat
from numpy import *
from IPython.display import Image
def load_picture():
    path='./data/bird_small.png'
    image=plt.imread(path)
    plt.imshow(image)
    plt.show()

def load_data():
    path='./data/bird_small.mat'
    data=loadmat(path)
    return data

def normalizing(A):
    A=A/255.
    A_new=reshape(A,(-1,3))
    return A_new

def get_near_cluster_centroids(X,centroids):
    m = X.shape[0] #数据的行数
    k = centroids.shape[0] #聚类中心的行数，即个数
    idx = zeros(m) # 一维向量idx，大小为数据集中的点的个数，用于保存每一个X的数据点最小距离点的是哪个聚类中心
    for i in range(m):
        min_distance = 1000000
        for j in range(k):
            distance = sum((X[i, :] - centroids[j, :]) ** 2) # 计算数据点到聚类中心距离代价的公式，X中每个点都要和每个聚类中心计算
            if distance < min_distance:
                min_distance = distance
                idx[i] = j # idx中索引为i，表示第i个X数据集中的数据点距离最近的聚类中心的索引
    return idx # 返回的是X数据集中每个数据点距离最近的聚类中心

def compute_centroids(X, idx, k):
    m, n = X.shape
    centroids = zeros((k, n)) # 初始化为k行n列的二维数组，值均为0，k为聚类中心个数，n为数据列数
    for i in range(k):
        indices = where(idx == i) # 输出的是索引位置
        centroids[i, :] = (sum(X[indices, :], axis=1) / len(indices[0])).ravel()
    return centroids

def k_means(A_1,initial_centroids,max_iters):
    m,n=A_1.shape
    k = initial_centroids.shape[0]
    idx = zeros(m)
    centroids = initial_centroids
    for i in range(max_iters):
        idx = get_near_cluster_centroids(A_1, centroids)
        centroids = compute_centroids(A_1, idx, k)
    return idx, centroids

def init_centroids(X, k):
    m, n = X.shape
    init_centroids = zeros((k, n))
    idx = random.randint(0, m, k)
    for i in range(k):
        init_centroids[i, :] = X[idx[i], :]
    return init_centroids

def reduce_picture():
    initial_centroids = init_centroids(A_new, 16)
    idx, centroids = k_means(A_new, initial_centroids, 10)
    idx_1 = get_near_cluster_centroids(A_new, centroids)
    A_recovered = centroids[idx_1.astype(int), :]
    A_recovered_1 = reshape(A_recovered, (A.shape[0], A.shape[1], A.shape[2]))
    plt.imshow(A_recovered_1)
    plt.show()

if __name__=='__main__':
    load_picture()
    data=load_data()
    print(data.keys())
    A=data['A']
    print(A.shape)
    A_new=normalizing(A)
    print(A_new)
    print(A_new.shape)
    reduce_picture()