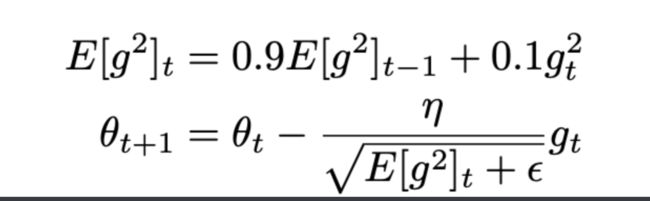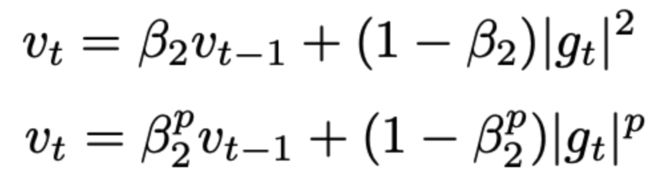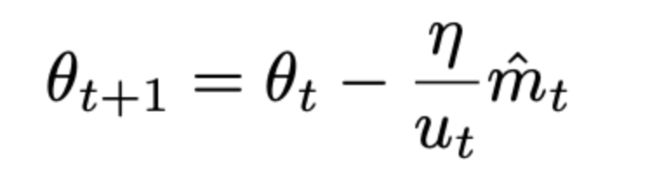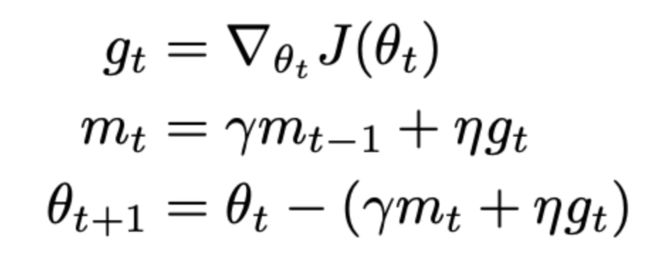深度学习框架TensorFlow系列之(五)优化器3
1 背景
梯度下降算法是目前最流行的优化算法之一,并且被用来优化神经网络的模型。业界知名的深度学习框架TensorFlow、Caffe等均包含了各种关于梯度下降优化算法的实现。然而这些优化算法(优化器)经常被用作黑盒优化器,造成对这些算法的优缺点以及适用场景没有一个全面而深刻的认知,可能造成无法在特定的场景使用最优解。
梯度下降法的的目标是在梯度的相反方向进行模型参数的更新,从几何学来说,就是沿着斜率的方向(最快)由目标函数创建的曲面一直向下直到山谷,并且通过合理的步长设置加快与稳定算法模型的收敛,训练出泛化更强的模型。基本思想亦可以这样理解:我们从山上的某一点出发,找一个最陡的坡走一步(也就是找梯度方向),到达一个点之后,再找最陡的坡,再走一步,直到我们不断的这么走,走到最“低”点(最小花费函数收敛点),但是实际的建模场景比较复杂,有鞍点以及局部低点的存在。基于此,相关科研人员针对该算法进行了广泛而深度的研究。
相关符号:
-
模型的代价函数: J ( θ ) J(\theta) J(θ)
-
模型的相关参数: θ ∈ R d \theta \in R^d θ∈Rd
-
参数的梯度: ▽ θ J ( θ ) \bigtriangledown_{\theta}J(\theta) ▽θJ(θ)
-
参数的梯度: η \eta η
本系列文章已经完成两篇《深度学习框架TensorFlow系列之(五》优化器1》和《深度学习框架TensorFlow系列之(五》优化器2》,在这两篇中,已经全面的介绍了优化器的相关知识,对随机梯度下降、批量与小批量梯度下降以及动量和学习率做了全面的介绍,本章重点介绍下几种在训练过程中,较为有效的几种高级的优化器特例。
2 NAG(Nesterov accelerated gradient)
2.1 场景分析
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QC58rzwg-1646569096714)(https://smy-img.hellonitrack.com/uploads/image/20210220/1613802863131293.jpg)]
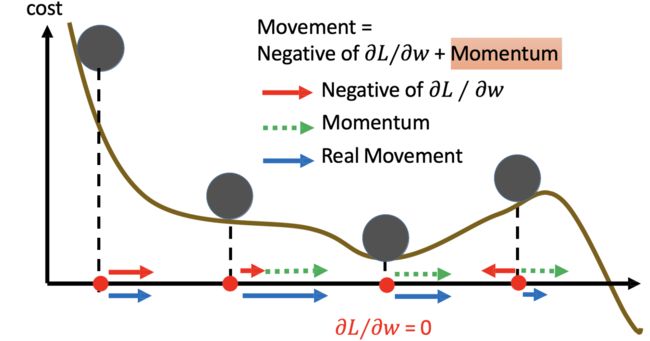
一个从坡顶向下形式的车辆,其动力来源于两个部分,一个是历史积累的冲量,一个是当前的力量,如果想要车在坡底停下而不是冲过坡地进入其他区域的话,需要一个阻力,并且这个阻力需要根据未来的坡度进行提前有感知与预判,在坡度即将放缓的时候,提前进行减速。
2.2 方案设计
从上面的描述中我们得知,我们需要一种感知与预测未来梯度变化趋势的方法。那么具体如何操作呢?
- 算法设计
该方案通过提前去预测参数下一步的位置,进而可以提前预判梯度更新的方向趋势。基于预测位置替换当前位置进行梯度计算,提前感知梯度方向变化,所以对于当前的方向有一定的修正作用,相当于对惯性加了个控制力,防止冲出谷底,使模型更加快速的收敛,防止摇摆。
- 第一步,预测参数下一步的更新位置,并且在更新后的位置求梯度,预测未来的梯度方向变化与强度;
- 第二步,计算历史动量,也就是累计下来的梯度值;
- 第三步,将第一步与第二步的梯度值进行矢量相加,作为待更新的梯度值;
- 第四步,将参数与第三步的梯度值进行计算;
- 公式如下
V t = γ V t − 1 + η ▽ θ J ( θ − γ V t − 1 ) V_t = \gamma V_{t-1} + \eta \bigtriangledown_{\theta}J(\theta - \gamma V_{t-1}) Vt=γVt−1+η▽θJ(θ−γVt−1)
θ = θ − V t \theta = \theta - V_t θ=θ−Vt
上面的图是对NAG的形象的描述,蓝色线段表示动量,蓝色短线表示当前位置梯度更新,蓝色长线表示之前累积的梯度;第一个红色线表示用NAG算法预测下一步位置的梯度更新,第一条棕色线表示先前累积的梯度,其矢量相加结果(绿色线)就是参数更新的方向。这种预见性更新防止我们走得太快,防止摇摆,提升模型训练的性能。
3 Adagrad
3.1 场景分析
机器学习模型随着模型的规模的不同,参数大小也大同小异,比如目前NLP领域的千亿乃至万亿的Bert以及GPT3等,那么这些参数的更新过程其实有很大的不同,比如训练数据中有些词频率非常低,那么对于这些词相关的参数的训练就不充分了;相反,对于某些高频词的相关的参数的训练就过于充分,由于整体训练的参数更新是所有参数同样的更新策略,所以造成模型训练的不充分。
其实不仅仅是NLP领域,搜广推的CTR、CVR模型领域都存在这样的问题,这种情况代表了一种训练过程中遇到的通用的问题,需要针对不同的参数采用不同的学习策略算法进行解决。
3.2 方案设计
- Adagrad算法的设计理念:
根据参数更新情况自适应调整学习率,对于不频繁更新的参数执行较大的学习率,对于频繁更新的参数执行较小的学习率。具体在实现的过程中,通过引入二阶动量,基于梯度变化的累计历史情况,进行学习率的校正与控制。
- 算法设计
-
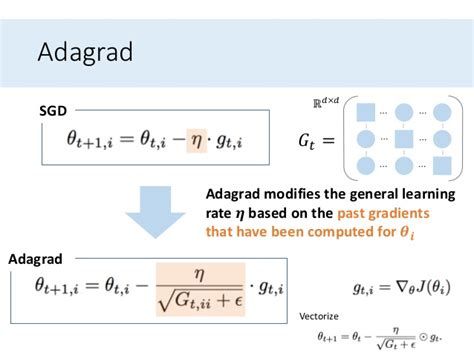
普通的优化器算法,例如SGD对所有参数 θ \theta θ进行统一更新,所以每个参数 θ \theta θ都使用相同的参数学习速率 η \eta η。而Adagrad算法对每个参数 θ i \theta_i θi在时间点t处使用不同的学习率$\eta 。 为 了 简 便 起 见 , 我 们 设 。为了简便起见,我们设 。为了简便起见,我们设g_{t,i} 为 时 间 点 t 时 对 参 数 为时间点t时对参数 为时间点t时对参数\theta_i$的梯度为:
g t , i = ▽ θ t J ( θ t , i ) g_{t,i} = \bigtriangledown_{\theta_t}J(\theta_t, i) gt,i=▽θtJ(θt,i)
-
TSGD算法在时间t的时候,同时更新所有的参数,公式如下:
θ t + 1 , i = θ t , i − η ∗ g t , i \theta_{t+1}, i = \theta_{t,i} - \eta * g_{t,i} θt+1,i=θt,i−η∗gt,i
-
基于自适应的弹性更新规则,Adagrad算法在每个时间点t更新每个参数的时候,根据过去累计的二阶动量的进行学习率的调整,公式如下:
θ t + 1 , i = θ t , i − η ( G t , i i + ϵ ) ∗ g t , i \theta_{t+1}, i = \theta_{t,i} - \frac{\eta}{\sqrt{(G_{t,ii} + \epsilon)}} * g_{t,i} θt+1,i=θt,i−(Gt,ii+ϵ)η∗gt,i
-
G t , i i G_{t,ii} Gt,ii是历史梯度平方累加和。对于训练数据少的特征,对应的参数更新就缓慢,也就是说他们的梯度变化平方累加和就会比较小,所以对应于上面参数更新方程中的学习速率就会变大,所以对于某个特征数据集少,相应参数更新速度就快。同时为了防止上述分母为0,所以往往添加一个平滑项参数 ϵ \epsilon ϵ,避免除零,通常大小在1e − 8。
3.3 Adagrad算法的优劣
下面介绍下Adagrad算法的优劣,以便于后续的改进;
- 优点是消除了手动调整学习速率的问题,实现自动化。其他优化器大多数实现使用默认值0.01,并保持不变。
- 缺点是在分母中积累了平方梯度:基于平方和所以每增加一步都积累一个正数,在训练过程中累积的总和不断增加。这反过来又导致学习速率逐渐减小,最终变得无穷小,此时算法不再能够获得额外的知识,无法进行训练。
4 Adadelta
针对Adagrad算法的缺陷,Adadelta算法进行改进。设计理念是对于各个参数学习率的控制不是基于过于梯度平方的累积,而是基于过去梯度平方的一个衰减加权均值,故可以避免造成学习率过小带来的无法有效训练的难题,
-
计算二阶动量的指数衰减加权值,基于历史累计梯度与当前的梯度,计算公式如下,可见历史梯度是不断的进行衰减的
E [ g 2 ] t = γ E [ g 2 ] t − 1 + ( 1 − γ ) g t 2 E[g^2]_t = \gamma E[g^2]_{t-1} + (1-\gamma) g_t^2 E[g2]t=γE[g2]t−1+(1−γ)gt2
-
从上面的Adagrad章节,我们知道参数更新公式如下:
θ t + 1 = θ t − η ( G t + ϵ ) ∗ g t \theta_{t+1} = \theta_{t} - \frac{\eta}{\sqrt{(G_{t} + \epsilon)}} * g_{t} θt+1=θt−(Gt+ϵ)η∗gt
-
将衰减加权值代入上面的公式,则公式改进为
θ t + 1 = θ t − η ( E [ g 2 ] t + ϵ ) ∗ g t \theta_{t+1} = \theta_{t} - \frac{\eta}{\sqrt{(E[g^2]_t + \epsilon)}} * g_{t} θt+1=θt−(E[g2]t+ϵ)η∗gt
-
由于分母是梯度的均方根误差的形式,所以我们定义一个新的简写形式
θ t + 1 = θ t − η R M S [ g ] t ∗ g t \theta_{t+1} = \theta_{t} - \frac{\eta}{RMS[g]_t} * g_{t} θt+1=θt−RMS[g]tη∗gt
-
至此,dagrad算法带来的分母越来越大的问题得以解决。但是作者注意到梯度更新中的单位(以及SGD、Momentum或Adagrad)没有匹配,即更新应该具有与参数相同的假设单位。那么为何单位不匹配呢?我们看下公式:
θ t + 1 = θ t − η ∗ ∂ ( l o s s ) ∂ ( θ t ) \theta_{t+1} = \theta_{t} -{\eta}* \frac{\partial(loss)}{\partial(\theta_t)} θt+1=θt−η∗∂(θt)∂(loss)
-
假设loss的单位为A,参数的单位为B,已知学习率没有单位,设为1,则上面的等式的单位运算为:B=B-1*(A/B)。可以看出单位确实不匹配。(这个问题确实是一个比较深刻的思考,很多人基本没有从这方面进行思考过)
-
为了保障单位的匹配,作者设计了非常精妙的方法,定义另一个指数衰减加权均值,与梯度的二阶动量计算类似,我们定义 △ θ \triangle \theta △θ的二阶动量的指数衰减加权均值。
E [ △ θ 2 ] t = γ E [ △ θ 2 ] t − 1 + ( 1 − γ ) △ θ 2 E[{\triangle \theta}^2]_t = \gamma E[{\triangle \theta}^2]_{t-1} + (1-\gamma) {\triangle \theta}^2 E[△θ2]t=γE[△θ2]t−1+(1−γ)△θ2
-
使用RMS进行化简;
R M S [ △ θ ] t = E [ △ θ 2 ] + ϵ RMS[{\triangle \theta}]_t= \sqrt{E[{\triangle \theta}^2] + \epsilon} RMS[△θ]t=E[△θ2]+ϵ
-
现在我们用用 R M S [ △ θ ] t − 1 RMS[{\triangle \theta}]_{t-1} RMS[△θ]t−1替换之前更新规则中的学习速率η,后生成Adadelta更新规则:
△ θ t = − R M S [ △ θ ] t − 1 R M S [ g ] t ∗ g t \triangle \theta_t = - \frac{RMS[{\triangle \theta}]_{t-1}}{RMS[g]_{t}}*g_t △θt=−RMS[g]tRMS[△θ]t−1∗gt
△ θ t + 1 = △ θ t + △ θ t \triangle \theta_{t+1} = \triangle \theta_{t} + \triangle \theta_t △θt+1=△θt+△θt
现在我们可以验证一下,方程中参数单位是否会匹配,**其中参数单位还是为B,loss单位为A,那么方程参数的单位运算有:B=B-[B/(A/B)]A/B,那么可以证明单位是匹配的。**使用Adadelta,从上面的公式我们可以看到,甚至不需要设置默认的学习速率。
5 RMSprop
RMSprop是由Geoff Hinton提出的一种未发表的自适应学习率方法。RMSprop和Adadelta都是在同一时期独立提出的,基本思路都是一致的。都是解决Adagrad急剧下降的学习速度的难题。公式如下:
RMSprop也将学习速率除以平方梯度的指数衰减平均值。Hinton建议将γ设置为0.9,而学习速率η默认值为0.001。
6 Adam
从上面的分析可以看到,我们目前在优化器是解决两类问题:
- 梯度历史动量如何累计与校正:梯度动量引入梯度更新(加权衰减累加等)、NAG提前的梯度方向预判算法;
- 学习率如何进行不同参数的自适应调整:这点从Adagrad、Adadelta与RMSprop中会得以体现。
那么有没有一种优化器是兼顾上面两个方面呢?答案就是Adam。
Adam全称Adaptive Moment Estimation(自适应矩估计),是一种将自适应学习率与动量累加梯度的算法,它将梯度历史动量自适应累计和Adadelta或RMSprop结合起来的算法,在学习率方面Adam保持了上面的梯度的指数衰减加权均值。
-
首先计算一阶与二阶动量累计值 m t m_t mt和 v t v_t vt。
m t = β 1 m t − 1 + ( 1 − β 1 ) g t m_t = \beta_1 m_{t-1} + (1- \beta_1)g_t mt=β1mt−1+(1−β1)gt
v t = β 2 v t − 1 + ( 1 − β 2 ) g t 2 v_t = \beta_2v_{t-1} + (1-\beta_2)g_t^2 vt=β2vt−1+(1−β2)gt2
-
当 m t m_t mt和 v t v_t vt被初始化为0的时候,Adam的作者观察到它们偏向于0,特别是当衰减率较大时(即β1和β2接近1)。所以作者重新计算一个偏差来抵消这些偏差:
m ^ t = m t 1 − β 1 t \hat{m}_t = \frac{m_t}{1-\beta_1^t} m^t=1−β1tmt
v ^ t = v t 1 − β 2 t \hat{v}_t = \frac{v_t}{1-\beta_2^t} v^t=1−β2tvt
-
最后进行参数的更新,就像我们在Adadelta和RMSprop中看到的那样生成Adam更新规则,并且通过使用一阶动量梯度累计值一起更新当前梯度(不同于Adadelta和RMSprop仅仅通过二阶动量控制学习率),添加了梯度的累计动量。
β t + 1 = β t − η v ^ t + ϵ ∗ m ^ t \beta_{t+1} = \beta_t - \frac{\eta}{\sqrt{\hat{v}_t + \epsilon}} * \hat{m}_t βt+1=βt−v^t+ϵη∗m^t
其中β1默认值为0.9,β2默认值为0.999,ε为10^-8,Adam集合动量和Adadelta两者的优点,从经验中表明Adam在实际中表现很好,并优于其他自适应学习方法算法。
7 AdaMax
Adamax算法相对于Adam本质没有太多变化,只是在计算的指数上有所调整,下面简单介绍下;
Adam更新规则中的系数与过去梯度 v t − 1 v_{t-1} vt−1(一阶)+ 现在梯度 g ( t ) 2 g(t)^2 g(t)2(二阶)成反比。作者提出是否可以考虑其他的P范数,也就是扩展到P阶动量,有方程式:
通常大的p值会造成数字不稳定,所以一般常用的都是L1和L2范数,但是而‘∞’也普遍表现出稳定的行为。由于这个原因作者提出了AdaMax[无穷动量],并证明了具有‘∞’的v收敛于下列更稳定的值,了避免与Adam混淆,我们用 u t u_t ut表示学习率优化约束 v t v_t vt:
则,参数更新的最终公式为
请注意,由于 u t u_t ut依赖于最大运算,它不像 m t m_t mt和 v t v_t vt那样容易偏向于零。这就是为什么我们不需要计算ut的偏差修正。好的默认值,η = 0.002, β1 = 0.9, β2 = 0.999。
8 Nadam
Adam将RMSprop和动量结合起来,但是没有基于未来变化趋势进行预测。我们在上面看到过NAG其实比单纯动量表现更好,因为它通过预测算法进行提前感知进行方向的校正。
Nadam(Nesterov-accelerated Adaptive Moment Estimation),Nesterov加速的自适应矩估计,将adam和NAG结合起来,为了将NAG添加到Adam,我们需要对动量部分进行一些改变。作者将NAG梯度更新公式变为:
也就是现在不再像NAG提前预测后面位置,而是直接在当前位置对当前梯度方向做两次更新,同样运用到Adam中需要对m做一个修正:
最终计算公式如下:
9 如何选择优化器
那么,应该使用哪种优化器呢?如果您的输入数据是稀疏的,使用上面的Adam可能是一个好的选择。另一个好处是你不需要需要调整学习速率,但使用默认值可能会取得最佳效果。
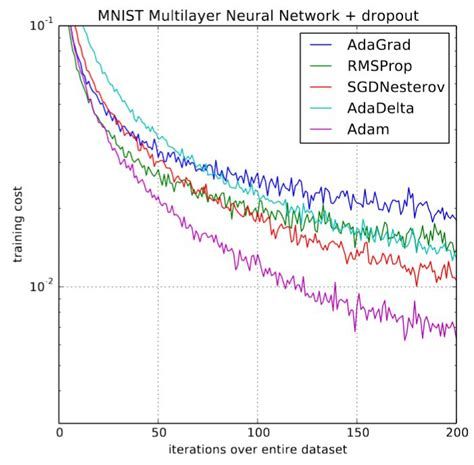
总之,RMSprop是Adagrad的一个扩展,处理其急剧减少的学习利率。它与Adadelta相同,除了Adadelta使用参数更新的RMS分子更新规则(参数的二阶动量与梯度的二阶动量相除)。最后,Adam为RMSprop添加了偏差修正和动量。所以RMSprop、Adadelta和Adam是非常相似的算法,它们在类似的环境下表现良好。实验证明具备偏差修正的Adam略微超过RMSprop走向。到目前为止,Adam可能是最好的选择。
有趣的是,有很多的论文使用的是普通的SGD,没有动量和简单的学习速率,使用学习率表。上面描述过SGD通常会找到一个最小值,但它可能需要比某些优化器运行更长时间,更依赖于健壮的初始化和学习率表,并可能卡在鞍点而不是局部最小值。因此,如果你关心快速收敛和训练深度或复杂的神经网络,你应该选择一种自适应学习率方法。
10 番外篇
个人介绍:杜宝坤,隐私计算行业从业者,从0到1带领团队构建了京东的联邦学习解决方案9N-FL,同时主导了联邦学习框架与联邦开门红业务。
框架层面:实现了电商营销领域支持超大规模的工业化联邦学习解决方案,支持超大规模样本PSI隐私对齐、安全的树模型与神经网络模型等众多模型支持。
业务层面:实现了业务侧的开门红业务落地,开创了新的业务增长点,产生了显著的业务经济效益。
个人比较喜欢学习新东西,乐于钻研技术。基于从全链路思考与决策技术规划的考量,研究的领域比较多,从工程架构、大数据到机器学习算法与算法框架均有涉及。欢迎喜欢技术的同学和我交流,邮箱:[email protected]