【机器学习】概念总结

一、绪论

基本术语

• 一组记录的集合称为一个数据集
• 每条记录是关于一个事件或者对象的描述，称为一个实例或者样本
• 反应事件或者对象在某方面的表现或者性质的事项称为属性或特征，属性上的取值称为属性值，属性张成的空间称为属性空间、样本空间或者输入空间
• 由于空间中的每个点都对应一个坐标向量，因此也把一个示例称为一个特征向量，每个示例由d个属性描述，d称为样本的维数
• 从数据中学得模型的过程称为学习或训练。训练过程中使用的数据称为训练数
  据，其中每个样本称为一个训练样本，训练样本组成的集合称为训练集
• 关于示例结果的信息称为标记 ，拥有了标记信息的示例称为样例，所有标记的集合称为标记空间或输出空间。
• 若预测的是离散值，此类学习任务称为分类;若预测的是连续值，此类学习任务称为回归
• 对只涉及两个类别的二分类任务,通常称其中-个类为正类 ，另一个为反类 ;涉及多个类别时，则称为多分类任务。
• 学得模型后，使用其进行预测的过程称为测试 ，被预测的样本称为测试样本。
• 聚类有助于我们了解数据的内在规律，能为更深入地分析数据建立基础。
• 根据训练数据是否拥有标记信息，学习任务可大致分为两大类:监督学习和无监督学习，分类和回归是前者的代表，而聚类则是后者的代表。
• 学得模型适用于新样本的能力，称为泛化能力。

归纳偏好

• 机器学习算法在学习过程中对某种类型假设的偏好，称为归纳偏好，或简称为偏好。任何一个有效的机器学习算法必有其归纳偏好。
• "奥卡姆剃刀”是-种常用的、自然科学研究中最基本的原则，
  即”若有多个假设与观察一致，则选最简单的那个”。
• 在具体问题现实问题中，算法的归纳偏好是否与问题本身匹配，大
  多数时候直接决定了算法能否取得好的性能。

假设空间

归纳与演绎是科学推理的两大基本手段。前者是从特殊到一般归纳与演绎是科学推理的两大基本手段。前者是从特殊到- -般性规律;后者则是从-般到特殊的“特化”过程，即从基础原理推演出具体状况。

二、模型评估与选择

经验误差与过拟合

错误率：分类错误的样本占样本总数的比例
误差：样本真实输出与预测输出之间的差异
训练(经验)误差：训练集上
测试误差：测试集
测试集：除训练集外所有样本
过拟合：学习器把训练样本本身特点当做所有潜在样本都会具有的一般性质.
欠拟合：训练样本的一般性质尚未被学习器学好.

评估方法

留出法：直接将数据集划分为两个互斥的部分，分层采样、随机划分，保留1/5~1/3作为测试集；

交叉验证法：将数据集划分为k个互斥的子集，其中k-1个作为训练集，1个作为测试集，将k次实验结果取平均值；

自助采样法：将数据集D有放回的采样m次得到训练集S，剩下的作为测试集T（仅在数据集较小时使用）(集成学习的bagging方法使用)；

性能度量

回归任务最常用的性能度量是“均方误差”
错误率：分类错误的样本占样本总数的比例
精度：分类正确的样本占样本总数的比例
统计真实标记和预测结果的组合可以得到“混淆矩阵”

查准率：预测为正的样本中真正为正的比例
查全率(召回率)：实际为正的样本中被预测为正的样本的比例
基于查准率和查全率可以绘制P-R曲线，查准率=查全率时候称为平衡点
F1度量：

ROC曲线：以“假正例率”为横轴，“真正例率”为纵轴
AUC值：是ROC曲线的面积，面积越大AUC值越大，性能越好

偏差与方差

偏差：描述了期望预测与真实结果之间的差异，刻画了训练器本身的泛化能力；

方差：描述了测试集的变化所带来的学习器性能的变化，刻画了数据扰动带来的影响；

噪声：描述了对于一个具体的任务任何算法学习结果的下界，刻画了一个具体问题本身的难度；

三、线性模型

优点在于计算代价低，易于逻辑实现，但是缺点在于容易欠拟合，分类精度低。

基础知识

线性模型：学得一个通过属性的线性组合来进行预测的函数
线性回归：学得一个线性模型以尽可能准确地预测实值输出标记，通过最小二乘法进行参数/模型的估计(单一属性的线性回归、多元属性的线性回归)
对数线性回归：用线性模型结果的对数形式去毕竟真实标记

二分类任务

对数几率回归：二分类任务中，模型的输出应该映射为0，1；理想情况下是使用单位阶跃函数，但是他的数学性质不友好，使用对数几率函数替代
线性判别分析（LDA）：不使用回归的思想，而是直接分类。二维好分类，但是高纬怎么操作呢？LDA就是解决这个问题的，将高维映射到低维就行了。
LDA的思想：
1、欲使同类样例的投影点尽可能接近，可以让同类样例投影点的协方差尽可能小
2、欲使异类样例的投影点尽可能远离，可以让类中心之间的距离尽可能大

多分类任务

二分类学习方法推广到多类（不常用）
利用二分类学习器解决多分类问题（常用）
思想：
1、对问题进行拆分，为拆出的每个二分类任务训练一个分类器
2、对于每个分类器的预测结果进行集成以获得最终的多分类结果
拆分策略：
1、一对一（One vs. One, OvO）
2、一对其余（One vs. Rest, OvR）
3、多对多（Many vs. Many, MvM）

四、决策树

优点是计算的复杂度不高，对中间值的缺失不敏感还可以处理不相关的特征数据，但是天生的缺点就是会出现过拟合问题；
常用算法：ID3（经典）、C4.5（最常用）、CART（可以用于回归任务）、RF随机森林（集成学习的结果，效果很强！）
决策树的基本思想是分治法，关键在于如何选择最优划分属性，使得节点的“纯度”最高（ID3信息增益越大，C4.5增益率最大，CART基尼指数越小）。

信息增益

“信息熵”：是度量样本集合纯度最常用的一种指标，信息熵越小，纯度越高

信息增益：划分前的信息熵减去划分后的信息熵，信息增益越大，则意味着使用该属性来进行划分所获得的“纯度提升”越大

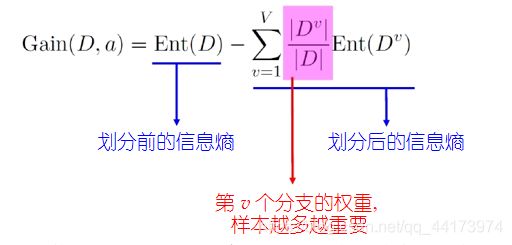
ID3决策树学习算法以信息增益为准则来选择划分属性
信息增益对可取值数目较多的属性有所偏好

增益率

但是，增益率准则对可取值数目较少的属性有所偏好
因此C4.5使用了一个启发式：先从候选划分属性中找出信息增益高于平均水平的属性，再从中选取增益率最高的

基尼指数

剪枝

目的：避免过拟合
基本策略：预剪枝和后剪枝，
预剪枝是指在划分节点之前对泛化性能进行估计，若当前节点的划分可以带来泛化性能的提升，则不进行剪枝，否则进行剪枝，预剪枝可以降低过拟合的风险，提高计算速度与性能，但是会增加欠拟合的风险；
后剪枝是指，在整棵决策树生长完成后，自底而上对节点进行考察，若把该节点对应的子树替换成叶子节点能带来泛化性能的提高，就将该子树替换为叶子节点，后剪枝也显著降低了过拟合的风险，带来泛化性能的提高而且由于预剪枝，但是训练时间开销大于预剪枝。

连续值处理

二分法：就是将属性使用 大于某个数值的作为一类，小于某个数值的作为另外一类 的规则进行划分，那么n-1种划分方式就可以把属性划分成n个离散值

缺失值处理

基本思路：样本赋权，权重划分

五、神经网络

NP神经元模型

NP神经元模型：当前神经元接受来自于前面n个神经元的信号输入，加权累加之后与阈值比较，通过激活函数处理得到输出
激活函数：理想的激活函数是单位阶跃函数，但是常用的是Sigmoid函数
感知机：感知机由两层神经元组成, 输入层接受外界输入信号传递给输出层, 输出层是M-P神经元，能容易的实现逻辑与、或、非，但是只能解决线性可分的问题
多层感知机：在输出层与输入层之间还有一层或者多层神经元, 被称之为隐层或隐含层, 隐含层和输出层神经元都是具有激活函数的功能神经元

多层前馈神经网络：

只需一个包含足够多神经元的隐层 , 多层前馈神经网络就能以任意精度逼近任意复杂度的连续函数
定义：每层神经元与下一层神经元全互联, 神经元之间不存在同层连接也不存在跨层连接
前馈：输入层接受外界输入, 隐含层与输出层神经元对信号进行加工, 最终结果由输出层神经元输出
学习：根据训练数据来调整神经元之间的“连接权”以及每个功能神经元的“阈值”

误差逆传播算法（BP）

流程：首先初始化（随机或者按照经验来）网络中所有神经元的连接权重与阈值，然后进行迭代，迭代过程为：首先计算当前网络对样本的输出值，然后计算输出层和隐层的梯度值，根据梯度下降算法更新连接权值和阈值，循环直到满足条件。

BP神经网络算法也使用梯度下降法，以单个样本的均方误差的负梯度方向对权重进行调节。可以看出：BP算法首先将误差反向传播给隐层神经元，调节隐层到输出层的连接权重与输出层神经元的阈值；接着根据隐含层神经元的均方误差，来调节输入层到隐含层的连接权值与隐含层神经元的阈值。

算法问题：常常会过拟合，且隐层的个数难以准确确定，一般使用试错法进行调整
缓解过拟合策略：
1、早停：在训练过程中，当训练误差降低，测试误差明显升高时就停止训练
2、正则化：在误差目标函数里加入一项描述网络复杂程度的值，例如连接权重与阈值的平方和

参数寻优

常见策略：不同的初始参数、模拟退火、随机扰动、遗传算法

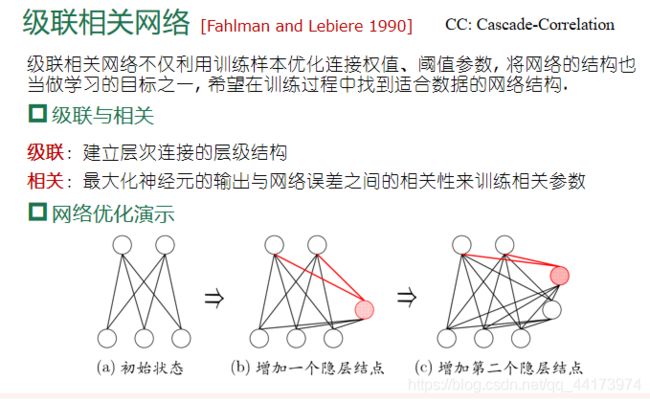
其他常见神经网络

RBF： 分类任务中除BP之外最常用，是一种单隐层前馈神经网络, 它使用径向基函数作为隐层神经元激活函数, 而输出层则是隐层神经元输出的线性组合.

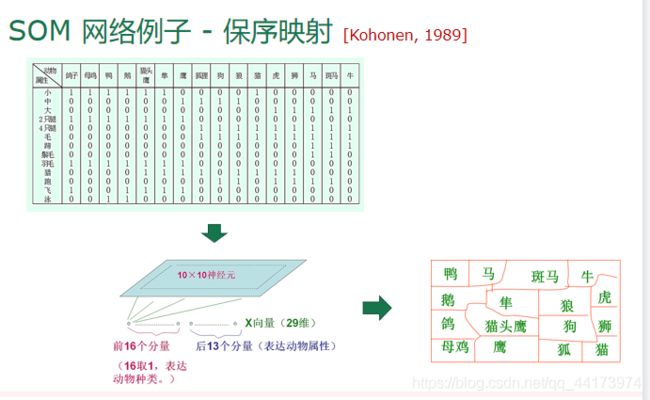
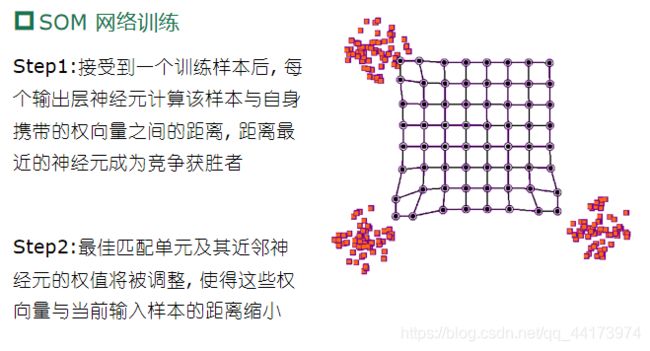
SOM：最常用的聚类方法之一，竞争型的无监督神经网络

• 将高维数据映射到低维空间（通常为 2维） , 高维空间中相似的样本点映射到网络输出层中邻近神经元
• 每个神经元拥有一个权向量
• 目标：为每个输出层神经元找到合适的权向量以保持拓扑结构
• 网络接收输入样本后，将会确定输出层的“获胜”神经元（“胜者通吃”），获胜神经元的权向量将向当前输入样本移动

级联相关网络

六、支持向量机

支持向量：就是从超平面出发，往外延申，直到碰到正负样本边缘的点，这些点就组成了支持向量
间隔：就是支持碰到正样本点边缘的支持向量和负样本点边缘的支持向量，所在超平面的距离，通俗点就是两个支持向量撑开的距离

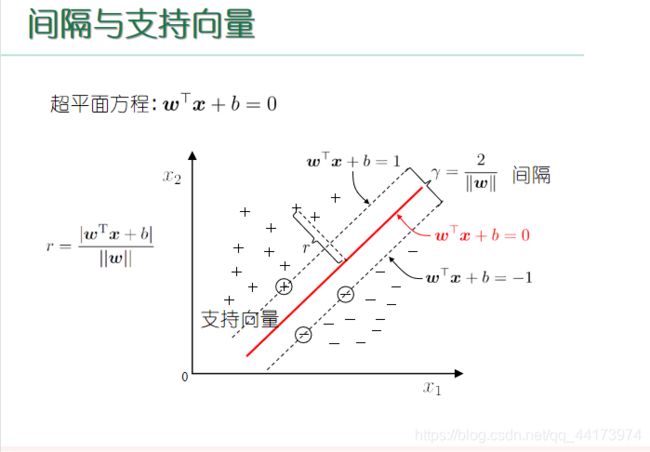
线性不可分

核映射：就是映射函数，用于将样本从原始空间映射到一个更高维的特征空间, 使得样本在这个特征空间内线性可分，且可证明：如果原始空间是有限维 (属性数有限)，那么一定存在一个高维特征空间使样本可分
推导可得，我们不需要显式地设计核映射, 而是设计核函数.
常用核函数：线性核函数（文本数据）、多项式核函数、高斯核函数（情况不明，就是高斯核）

软间隔和损失

现实中, 很难确定合适的核函数使得训练样本在特征空间中线性可分; 同时一个线性可分的结果也很难断定是否是因过拟合造成的
所以引入”软间隔”的概念, 允许支持向量机在一些样本上不满足约束.
但是为了使得不满足约束的样本点少，添加了损失函数去进行惩罚
最简单的想法是使用0/1损失函数，但是数学型态不好，可以采用一些数学性质好，一般选择0/1损失函数的上界，如hinge损失函数

正则化

支持向量回归

特点: 允许模型输出和实际输出间存在 的偏差.

七、贝叶斯分类器

我们前面学习的其实都是判别式模型，即直接根据观察到的样本特点去推测样本属于哪一类；而贝叶斯分类器则属于生成式模型，先对各种类别下，属性的特点建模，再基于贝叶斯公式去计算属于某个类别的概率，选择概率最大的作为预测的输出

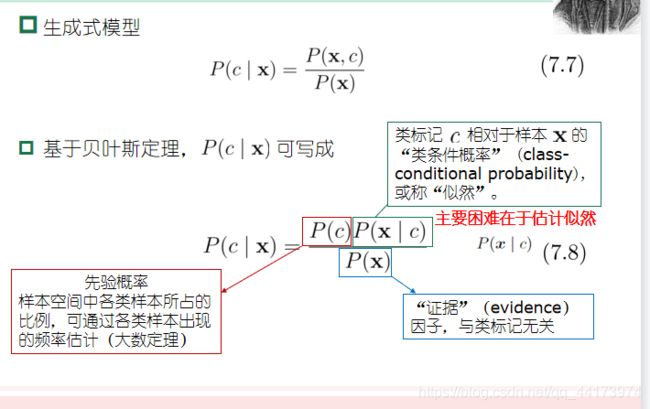
但是，联合概率不好算，属性可能很多，且分布未知，独立性未知

朴素贝叶斯分类器

假设：属性、取值都全部独立！

基于大数定理，用样本频率去估算概率就可以得到计算公式了

例子：

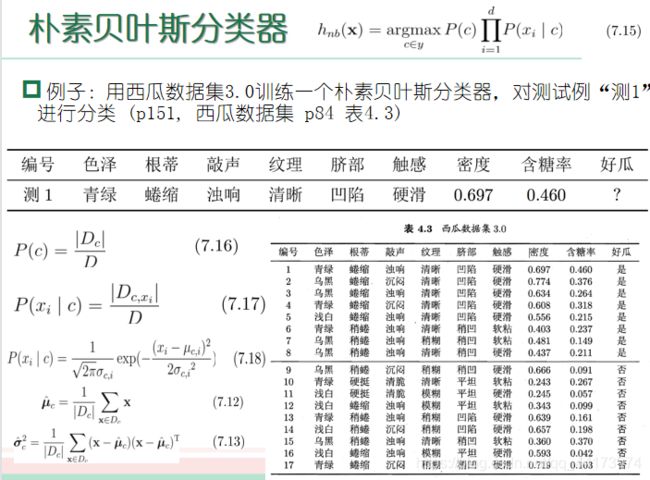
拉普拉斯修正：为了避免其他属性携带的信息被训练集中未出现的属性值“抹去”，人为再计算时候增加属性出现的个数

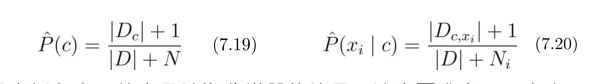
使用技巧：

• 若对预测速度要求高：预计算所有概率估值，使用时“查表”
• 若数据更替频繁：不进行任何训练，收到预测请求时再估值（懒惰学习）
• 若数据不断增加：基于现有估值，对新样本涉及的概率估值进行修正（增量学习）

半朴素贝叶斯分类器

假设：每个属性在类别之外最多仅依赖一个其他属性

贝叶斯网

借助有向无环图来刻画属性间的依赖关系，并使用条件概率表来表述属性的联合概率分布。
结构、学习还蛮复杂的，我赌一百块这个不考

推理的时候可以精确推断，即直接根据贝叶斯网定义的联合概率分布来精确计算后验概率，很困难；也可以近似推断，降低精度要求，在有限时间内求得近似解
方法：吉布斯采样

训练样本的某些属性的变量值未知怎么办？EM算法，实在理解不动了，考到就算了吧

八、集成学习

基础

集成的泛化性能通常显著优于单个学习器的泛化性能
集成个体应该好而不同；个体学习器要有一定的准确性和多样性，学习器间要有差异性

集成学习：通过构建并结合多个学习器来提升性能
同质集成：集成中只包含同种类型的“个体学习器”（基学习器），相应的学习算法称为“基学习算法”
异质集成：个体学习器由不同的学习算法生成不存在“基学习算法”

集成学习两类方法：序列化方法和并行化方法，两者的典型代表是AdaBoost和Bagging

Boosting

• 个体学习器存在强依赖关系，
• 串行生成
• 每次调整训练数据的样本分布

通俗解释：对于数据集的数据，先给第一个学习器，给分错的样本加权，再给下一个分类器，然后持续这个过程，直到到达最后一个学习器
从偏差-方差的角度：降低偏差，可对泛化性能相当弱的学习器构造出很强的集成

Bagging

• 个体学习器不存在强依赖关系
• 并行化生成
• 自助采样法

通俗解释：每个学习器都通过自助采样从训练集中获取数据，然后分别学习，对于新来的样本，投票选择类别
从偏差-方差的角度：降低方差，在不剪枝的决策树、神经网络等易受样本影响的学习器上效果更好

多样性度量方式

不合度量、相关系数、Q-统计量、K-统计量

多样性增强

• 数据样本扰动，例如 Adaboost 使用 重要性采样、Bagging 使用自助采样，对“不稳定基学习器” (如决策树、神经网络等 ) 不适用于“稳定基学习器” （如线性分类器、SVM、朴素贝叶斯等）
• 输入属性扰动，例如 随机子空间，典型就是随机森林算法
• 输出表示扰动
• 算法参数扰动

九、聚类

基础

目标：将数据集中的样本划分为若干个通常不相交的子集（簇）
作用：聚类既可以作为一个单独过程（用于找寻数据内在的分布结构）， 也可作为分类等其他学习任务的前驱过程.

性能度量：外部指标（将聚类结果与某个“参考模型”(reference model) 进行比较），内部指标（直接考察聚类结果而不用任何参考模型）
基本想法：“簇内相似度”高且“簇间相似度”低

距离计算：使用闵可夫斯基距离，p=2：欧氏距离，p=1：曼哈顿距离

原型聚类

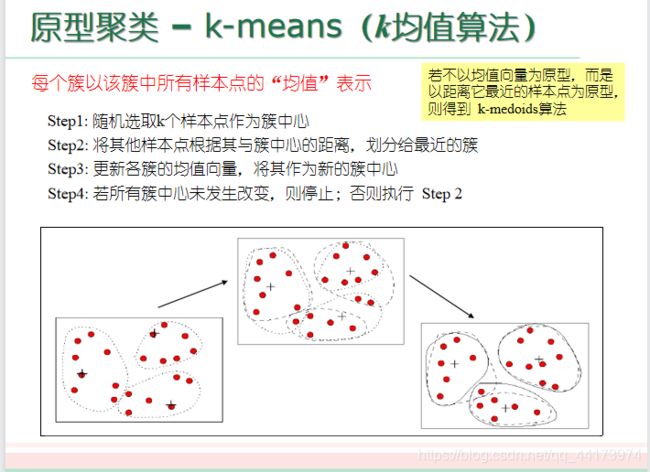
k-means（k均值算法）

简单，但是效果没那么好，就是以均值为中心画圆，适用性不广

学习向量量化（LVQ）

思想： 与一般聚类算法不同的是，LVQ假设数据样本带有类别标记，学习过程中利用样本的这些监督信息来辅助聚类.

高斯混合聚类

思想：采用概率模型来表达聚类原型，假设样本分布是由K个高斯分布叠加得到的

密度聚类

思想：假设聚类结构能通过样本分布的紧密程度来确定

层次聚类

思想：层次聚类试图在不同层次对数据集进行划分，从而形成树形的聚类结构。

十、降维

k近邻学习

朴素理解：就是把预测样本直接丢进训练集，找到最近的K个样本，然后投票就好了
优点：简单，且泛化错误率不超过贝叶斯最优分类器错误率的两倍

懒惰学习：此类学习技术在训练阶段仅仅是把样本保存起来，训练时间开销为零，待收到测试样本后再进行处理。
急切学习： 在训练阶段就对样本进行学习处理的方法。

降维

要满足密采样条件所需的样本数目是无法达到的天文数字
维数灾难：在高维情形下出现的数据样本稀疏、距离计算困难等问题
方法：

• 多维缩放（MDS），要求原始空间中样本之间的距离在低维空间中得以保持
• 线性变换，对原始高维空间进行线性变换进行降维，这个是线代！终于发现能作为线代大题考的原因了
• 主成分分析（PCA），对于正交属性空间中的样本点，用一个超平面对所有样本进行恰当的表达。通俗解释：以xyz为例，样本点落在这个空间中，但是他们之间的关系很难用xyz描述，但是我们观察发现他们是在一个平面上的，于是我们可以对这个平面进行分析，引入新的变量dx和dy，用于描述这个平面，找到dx和dy与样本点的关系之后，我们再将dx dy转换为xyz，就得到了原样本点和xyz的关系
• 核化线性降维,线性降维方法假设从高维空间到低维空间的函数映射是线性的，然而，在不少现实任务中，可能需要非线性映射才能找到恰当的低维嵌入
• 核化线性降维,因为当前空间内可能找到不到这样一个超平面，但是通过核函数升维之后，一定能找到，找到之后，再用PCA