派大汤的数据结构笔记---树与二叉树
数据结构笔记
- 五、树与二叉树
-
- 1. 树的基本概念
-
- 1.1 树的定义
- 1.2 基本术语
- 1.3 树的性质
- 2. 二叉树的概念
-
- 2.1 二叉树的定义及其主要特性
-
- 2.1.1 二叉树的定义
- 2.1.2 几种特殊的二叉树
- 2.1.3 二叉树的性质
- 2.2 二叉树的存储结构
-
- 2.2.1 顺序存储结构
- 2.2.2 链式存储结构
- 3. 二叉树的遍历和线索二叉树
-
- 3.1 二叉树的遍历
-
- 3.1.1 先序遍历
- 3.1.2 中序遍历
- 3.1.3 后序遍历
- 3.1.4 层次遍历
- 3.1.5 由遍历序列构造二叉树
- 3.2 线索二叉树
-
- 3.2.1 基本概念
- 3.2.2 中序线索二叉树
- 3.2.3 先序线索二叉树
- 3.2.4 后序线索二叉树
- 4. 树与森林
-
- 4.1 树的存储结构
-
- 4.1.1 双亲表示法
- 4.1.2 孩子表示法
- 4.1.3 孩子兄弟表示法(二叉树表示法)
- 4.2 树、森林与二叉树的转化
- 4.3 树与森林的遍历
-
- 4.3.1 树的先根遍历
- 4.3.2 树的后根遍历
- 4.3.3 树的层次遍历
- 4.3.4 森林的先序遍历
- 4.3.4 森林的中序遍历
- 5. 树与二叉树的应用
-
- 5.1 二叉排序树
-
- 5.1.1 二叉排序树的定义
- 5.1.2 二叉排序树的查找
- 5.1.3 二叉排序树的插入
- 5.1.4 二叉排序树的构造
- 5.1.5 二叉排序树的删除
- 5.1.6 查找效率分析
- 5.2 平衡二叉树
-
- 5.2.1 平衡二叉树的定义
- 5.2.2 平衡二叉树的插入(旋转)
-
- LL平衡旋转
- RR平衡旋转
- LR平衡旋转
- RL平衡旋转
- 5.2.3 平衡二叉树的查找
- 5.3 哈夫曼树与哈夫曼编码
-
- 5.3.1 哈夫曼树的定义
- 5.3.2 哈夫曼树的构造
- 5.3.3 哈夫曼编码
五、树与二叉树
1. 树的基本概念
1.1 树的定义
树是n个结点的优先级。当n=0时,称为空树。任意非空树应该满足:
- 有且只有一个特定的称为根的结点
- 当n>1时,其余节点可分为m(m>0)个互不相交的有限集 T 1 T_1 T1、 T 2 T_2 T2、 T 3 T_3 T3… T m T_m Tm,其中每个集合本身又是一个树,并且称为根的子树。
树的定义是递归的,即在树的定义中有用到了其自身,所以树是一种递归的数据结构。树作为一种逻辑结构,同时也是分层结构,具有以下特点:
- 树的根结点没有前驱,除根结点外的所有节点有且只有一个前驱。
- 树中所有结点可以有0个或者多个后继。
树中的某个结点(除根结点外)最多只和上一层的一个结点(父节点)有直接关系,根结点没有直接上层结点,所以n个结点的树有n-1条边。树中每个节点与下一层的0个或者多个结点(子女结点)有直接关系。
1.2 基本术语
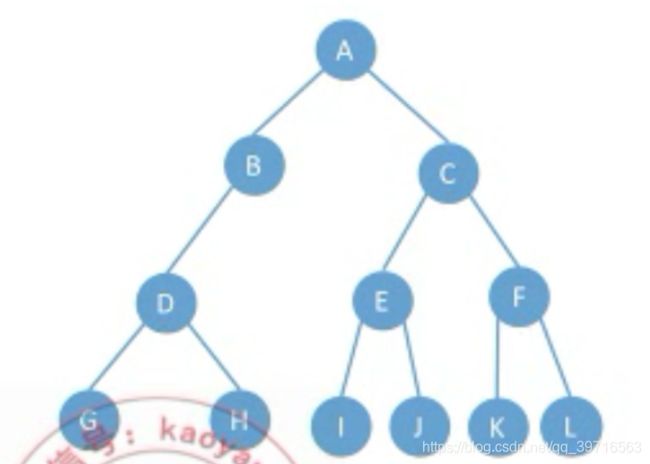
- 祖先结点:根结点到某结点的唯一路径上的任意结点。A、B是E的祖先。
- 子孙结点:从某结点出发,其所有路径上的所有结点都是该结点的子孙结点。E是A、B的子孙。
- 双亲结点(父节点):一个结点的直接前驱结点。B是E的双亲结点。
- 孩子结点:一个结点的直接后继。E是B的孩子结点。
- 兄弟结点:有相同双亲的结点称为兄弟结点。E、F是兄弟结点。
- 堂兄弟结点:双亲在同一层的结点互为堂兄弟。E、F、G、H、I、J是堂兄弟结点。
- 路径:树的两个结点之间所经过结点序列,树的分支是有方向的,即从双亲到孩子(从上到下),所以同一双亲的两个孩子之间不存在路径。
- 路径长度:路径上所经过的边的个数。
- 树的路径长度:从树的根结点到每个结点的路径长度的总和。
树与结点的属性:
- 结点的深度:自根结点开始自顶向下逐层累加。
- 结点的高度:自叶结点开始自底向上逐层累加。
- 树的高度(深度):树中结点的最大层数。
- 结点的度:有几个孩子(分支)。
- 树的度:各结点的度的最大值。
- 分支结点(非终端结点):度大于0的结点。
- 叶子结点(终端结点):度为0的结点。
有序树和无序树:
- 有序树:逻辑上看,树中结点的各子树从左到右是有次序的,不能互换。
- 无序树:逻辑上看,树中结点的各子树从左到右树无次序的,可以互换。
森林:森林是m(m>=0)棵互不相交的树的集合,特别地,m为0为空森林。
1.3 树的性质
- 性质1:结点数=总度数+1.
- 性质2:度为m的树中第i层上至多有 m i − 1 m^{i-1} mi−1个结点(i>=1)。
- 性质3:高度为h的m叉树至多有 m h − 1 m − 1 \frac{m^h-1}{m-1} m−1mh−1个结点,至少有h个结点。高度为h的度为m的树至多有 m h − 1 m − 1 \frac{m^h-1}{m-1} m−1mh−1个结点,至少有h+m-1个结点。
- 性质4:具有n个结点的m叉树的最小高度为[ l o g m ( n ( m − 1 ) + 1 ) log_m(n(m-1)+1) logm(n(m−1)+1)]。
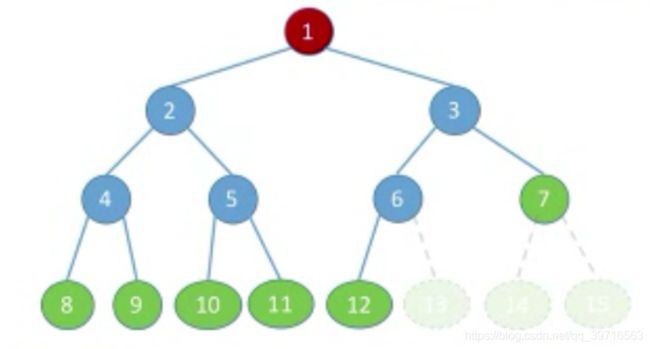
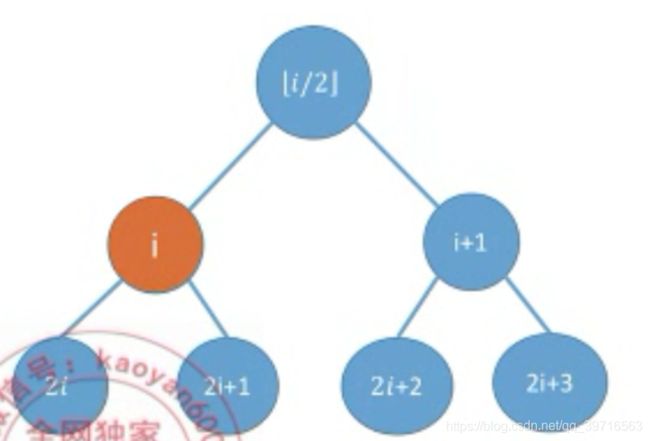
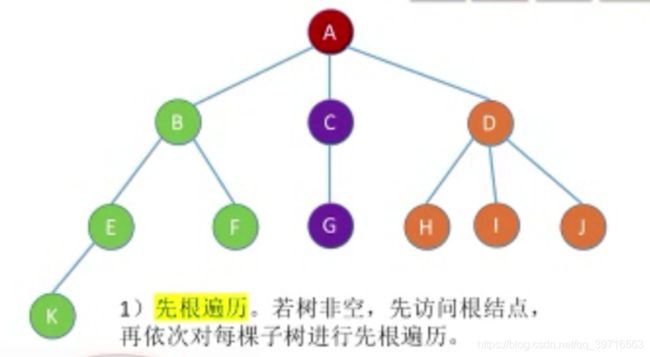
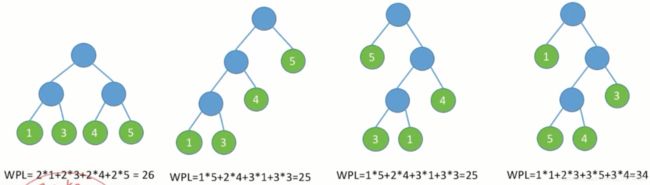
注意:度为m的树,m叉树的区别: 二叉树是n(n>=0)个结点的有限集合: 特点: 二叉树的五种状态: 满二叉树:一棵高度为h,且含有 2 h − 1 2^h-1 2h−1个结点的二叉树 完全二叉树:当且仅当其每个结点都与高度为h的满二叉树中编号为1-n的结点一一对应时称为完全二叉树。 二叉排序树:一个空二叉树或者是具有以下性质的二叉树: 性质一:设非空二叉树中度为0、1和2的结点个数分别是 n 0 n_0 n0、 n 1 n_1 n1、 n 2 n_2 n2,则 n 0 n_0 n0= n 2 n_2 n2+1(叶子结点比二分之结点多一个) 推导过程: 再由②-①得: n 0 n_0 n0= n 2 n_2 n2+1 性质二:二叉树中第i层上至多有 2 i − 1 2^{i-1} 2i−1个结点(i>=1) 性质三:高度为h的二叉树至多有 2 h − 1 2^h-1 2h−1个结点。 性质四:具有n(n>0)个结点的完全二叉树的高度h为[ l o g 2 ( n + 1 ) log_2(n+1) log2(n+1)] 或者 [ l o g 2 ( n ) log_2(n) log2(n)]+1 。 性质五:对于完全二叉树,设度为0、1、2的结点分别为 n 0 n_0 n0、 n 1 n_1 n1、 n 2 n_2 n2 推导过程: 所以亦可得结论,当一共有奇数(2k+1)个结点时,为了使得 n 0 n_0 n0+ n 1 n_1 n1+ n 2 n_2 n2为奇数, n 1 n_1 n1必为偶数,所以 n 1 n_1 n1=0。 顺序存储:指用一组连续的存储单元依次自上而下、自左而右存储完全二叉树上的结点元素。 二叉树的顺序存储结构只适合存储完全二叉树,当高度为h且只有h个结点的单支树(所有结点都为右孩子),顺序存储普通二叉树浪费空间太多,不做讨论。 结构体定义: 初始化操作: 链式存储:二叉链表至少包含三个域:数据域data,左指针域lchild、右指针域rchild。 结构体定义: 插入根结点: 三叉链表:数据域data,左孩子lchild,右孩子rchild,父结点指针*parent。 引入原因:查找某结点的父节点时,只能从根结点开始遍历查找。 先序遍历(PreOrder)过程: 若二叉树为空,则不进行遍历;否则, 递归算法: 中序遍历(InOrder)过程: 若二叉树为空,则不进行遍历;否则, 递归算法: 后序遍历(PostOrder)过程: 若二叉树为空,则不进行遍历;否则, 递归算法: 注意:三种遍历算法的时间复杂度为O(n),空间复杂度为O(n) 结合前面所学的栈在表达式中的应用: 层次遍历: 按照树的层次顺序,对二叉树的各个结点进行访问。 算法思想: 代码如下: 核心要义:一个遍历序列可能对应多种二叉树形态 case1:已知前序、中序遍历序列 若已知:前序遍历序列为DAEFBCHGI,中序遍历序列为EAFDHCBGI,求二叉树。 解答:由前序遍历序列可知根结点为D,再由中序遍历序列可知其左右子树分别为EAF、HCBGI。再由前序遍历得左子树根结点为A,右子树根结点为B。依次类推,可得二叉树为: case2:已知后序、中序遍历序列 若已知:后序遍历序列为EFAHCIGBD,中序遍历序列为EAFDHCBGI,求二叉树。 解答:由后序遍历序列可知根结点为D,再由中序遍历序列可知其左右子树分别为EAF、HCBGI。再由后序遍历得左子树根结点为A,右子树根结点为B。依次类推,可得二叉树为: 若已知:层序遍历序列为DABEFCGHI,中序遍历序列为EAFDHCBGI,求二叉树。 解答:由层序遍历序列可知根结点为D,再由中序遍历序列可知其左右子树分别为EAF、HCBGI。再由层序遍历得左子树根结点为A,右子树根结点为B。依次类推,可得二叉树为: 引入线索二叉树原因:若已知普通二叉树的某个结点,则不方便找到其前驱结点。必须从根结点开始遍历。 若无左子树,令lchild指向其前驱结点;若无右子树,令rchild指向其后继结点。利用其n+1个空链域指向其前驱、后继结点。 结点结构: 附设标志域,含义: r t a g { 0 rchild域指示结点的右孩子 1 rchild域指示结点的后继 rtag \begin{cases} 0& \text{rchild域指示结点的右孩子}\\ 1& \text{rchild域指示结点的后继} \end{cases} rtag{01rchild域指示结点的右孩子rchild域指示结点的后继 结构体定义: 递归算法 遍历方法 代码实现 找前驱 代码实现 遍历方法 找前驱 遍历方法 找前驱 结构体定义: 将每个结点的都用单链表连接起来形成线性结构,n个结点就有n个孩子链表(叶子结点的孩子链表为空表) 结构体定义: 将二叉链表作为树的存储结构,每个结点包括三部分内容。 结构体定义: 本质:用二叉链表存储森林。 森林转化为二叉树的步骤: 二叉树转化为森林的步骤: 遍历方法:若树非空,访问根结点,再依次访问每一个子树,按照这种方法遍历完整个树。最后得到的序列与对应二叉树的先序序列相同。 遍历方法:若树非空,先访问每一个子树,再依次访问根结点,按照这种方法遍历完整个树。最后得到的序列与对应二叉树的先中序列相同。 遍历方法: 遍历步骤: 效果等同于对每个树进行先根遍历,或者是将森林转换为与之对应的二叉树,再对二叉树进行先序遍历。 遍历步骤: 效果等同于对每个树进行后根遍历,或者是将森林转换为与之对应的二叉树,再对二叉树进行中序遍历。 二叉排序树(二叉查找树)或者是一棵空树,或者是具有以下特性的二叉树: 查找方法: 结构体定义: 查找代码: 插入方法: 若二叉树非空则直接插入根结点;否则,k小于根结点插入左子树,k大于根结点的值插入右子树。 插入代码: 构造方法: 删除方法: 查找长度:查找过程中,需要比对关键字的次数称为查找长度,反映了查找操作的时间复杂度。 平均查找长度ASL(Average Search Length) 查找成功最好情况:n个结点的二叉树最小高度为 l o g 2 n + 1 log_2n+1 log2n+1,平均查找长度为:O( l o g 2 n log_2n log2n) 平衡二叉树(平衡树/AVL舒):树上任意结点的左子树与右子树的高度之差不超过1. 结点的平衡因子:该结点的左子树高度-该结点的右子树高度 PS:平衡二叉树的每个结点的平衡因子值只可能是-1、0、1 插入->不平衡->旋转 每次调整的对象都是最小的不平衡树。 旋转步骤: 插入情形: 在结点的左孩子(L)的左子树(L)上插入了新的结点,并使得以这个结点为根结点的树成为最小不平衡子树。 旋转方法: 将结点的左孩子旋转为最小不平衡树的根结点,然后正常处理新结点的右子树即可。 插入情形: 在结点的右孩子®的右子树( R)上插入了新的结点,并使得以这个结点为根结点的树成为最小不平衡子树。 旋转方法: 将结点的右孩子旋转为最小不平衡树的根结点,然后正常处理新结点的左子树即可。 插入情形: 在根结点的左孩子(L)的右子树 ( R)上插入了新的结点,并使得以这个结点为根结点的树成为最小不平衡子树。 旋转方法: 先将根结点的右子树结点左上转为根结点的左孩子(左旋转),再将根结点左孩子右上转为根结点(右旋转),最后正常处理夹在根结点中间的子树。 插入情形: 在根结点的右孩子®的左子树 ( L)上插入了新的结点,并使得以这个结点为根结点的树成为最小不平衡子树。 旋转方法: 先将根结点的右子树结点右上转为根结点的右孩子(右旋转),再将根结点右孩子左上转为根结点(左旋转),最后正常处理夹在根结点中间的子树。 查找过程中,比较的次数不超过树的深度。 递推可得, n h n_h nh= n h − 1 n_{h-1} nh−1+ n h − 2 n_{h-2} nh−2+1 结点的权:结点上有现实含义的值 W P L = ∑ i = 1 n w i l i WPL= \sum_{i=1}^n w_il_i WPL=i=1∑nwili 所以上图中第2、3棵树为哈夫曼树,也称为最优二叉树。
二者都要满足任意结点的度<=m,即最多m个孩子。但是前者至少需要一个结点的度为m,后者允许所有结点的度都2. 二叉树的概念
2.1 二叉树的定义及其主要特性
2.1.1 二叉树的定义
2.1.2 几种特殊的二叉树
特点:
 特点:
特点:
二叉排序树:树上任意一个结点的左子树和右子树的深度之差不超过1。

2.1.3 二叉树的性质
假设树中结点的总数为n,则
①n= n 0 n_0 n0+ n 1 n_1 n1+ n 2 n_2 n2
②n= n 1 n_1 n1+2 n 2 n_2 n2+1 (树的结点数=总度数+1)
m叉树中第i层上至多有 m i − 1 m^{i-1} mi−1个结点(i>=1)
高度为h的m叉树至多有 m h − 1 m − 1 \frac{m^h-1}{m-1} m−1mh−1个结点。
①若完全二叉树有2k(偶数)个结点,则必有 n 1 n_1 n1=1, n 0 n_0 n0=k, n 2 n_2 n2=k-1。
②若完全二叉树有2k+1(奇数)个结点,则必有 n 1 n_1 n1=0, n 0 n_0 n0=k, n 2 n_2 n2=k-1。
设结点总数为n,则可知n= n 0 n_0 n0+ n 1 n_1 n1+ n 2 n_2 n2,且完全二叉树至多只有1个结点,所以可知 n 1 n_1 n1=1或者 n 1 n_1 n1=0。
由性质一可知: n 0 n_0 n0= n 2 n_2 n2+1,两边同时加 n 2 n_2 n2可得: n 0 n_0 n0+ n 2 n_2 n2=2 n 2 n_2 n2+1
易知: n 0 n_0 n0+ n 2 n_2 n2一定为奇数。
所以可得结论,当一共有偶数(2k)个结点时,为了使得 n 0 n_0 n0+ n 1 n_1 n1+ n 2 n_2 n2为偶数, n 1 n_1 n1必为奇数,所以 n 1 n_1 n1=1。
再得将 n 0 n_0 n0= n 2 n_2 n2+1代入2k= n 0 n_0 n0+ n 1 n_1 n1+ n 2 n_2 n2,可得 n 2 n_2 n2=k-1, n 0 n_0 n0=k。
综上所述,若完全二叉树有2k(偶数)个结点,则必有 n 1 n_1 n1=1, n 0 n_0 n0=k, n 2 n_2 n2=k-1。
再得将 n 0 n_0 n0= n 2 n_2 n2+1代入2k+1= n 0 n_0 n0+ n 1 n_1 n1+ n 2 n_2 n2,可得 n 2 n_2 n2=k, n 0 n_0 n0=k。
综上所述,若完全二叉树有2k+1(奇数)个结点,则必有 n 1 n_1 n1=1, n 0 n_0 n0=k, n 2 n_2 n2=k。2.2 二叉树的存储结构
2.2.1 顺序存储结构
#define MaxSize 100
struct TreeNode{
int value;
bool isEmpty;
};
void InitTree(TreeNode t[MaxSize]){
for(int i=0;i<MaxSize;i++){
t[i].isEmpty=true;
}
}
2.2.2 链式存储结构
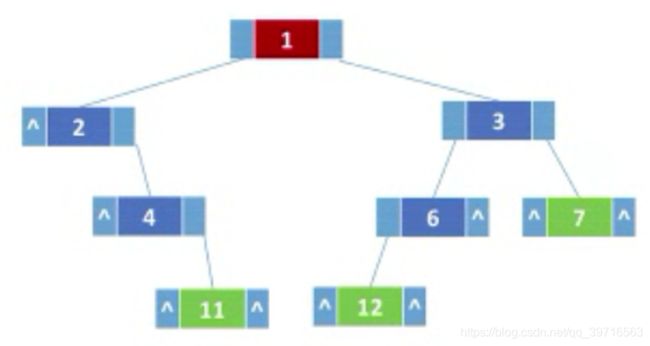
重要结论:在含有n个结点的二叉链表中,含有n+1个空链域,经常利用空链域来组成另一种链表结构—线索链表。typedef struct BiTNode{
int data ;
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
void InsertRootNode(BiTree root){
root=(BiTree )malloc (sizeof(BiTNode));
root->data=1;
root->lchild=NULL;
root->rchild=NULL;
}
typedef struct BiTNode{
int data ;
struct BiTNode *lchild,*rchild;
struct BiTNode *parent;
}BiTNode,*BiTree;
3. 二叉树的遍历和线索二叉树
3.1 二叉树的遍历
3.1.1 先序遍历
void PreOrder(BiTree T){
if (T!=NULL){
visit(T);
PreOrder(T->lchild);
PreOrder(T->rchild);
}
}
3.1.2 中序遍历
void InOrder(BiTree T){
if (T!=NULL){
InOrder(T->lchild);
visit(T);
InOrder(T->rchild);
}
}
3.1.3 后序遍历
void PostOrder(BiTree T){
if (T!=NULL){
PostOrder(T->lchild);
PostOrder(T->rchild);
visit(T);
}
}
先序遍历->前缀表达式
中序遍历->中缀表达式
后序遍历->后缀表达式3.1.4 层次遍历
void LevelOrder(BiTree T){
LinkQueue Q;
InitQueue(Q);
BiTree p;
EnQueue(Q,T);
while (!IsEmpty(Q)){
DeQueue(Q,p);
visit(p);
if (p->lchild!=NULL){
EnQueue(p->lchild);
}
if (p->rchild!=NULL){
EnQueue(p->rchild);
}
}
}
3.1.5 由遍历序列构造二叉树


3.2 线索二叉树
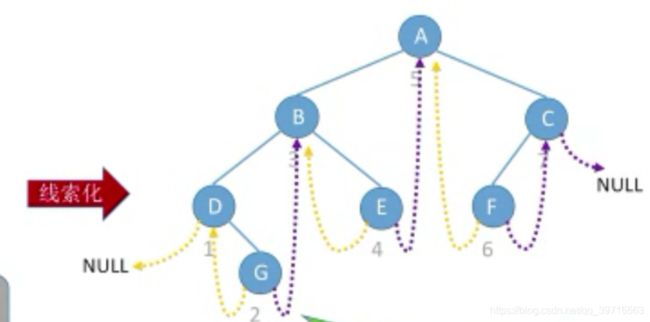
3.2.1 基本概念
lchild
ltag
data
rtag
rchild
l t a g { 0 lchild域指示结点的左孩子 1 lchild域指示结点的前驱 ltag \begin{cases} 0& \text{lchild域指示结点的左孩子}\\ 1& \text{lchild域指示结点的前驱} \end{cases} ltag{01lchild域指示结点的左孩子lchild域指示结点的前驱typedef struct ThreadNode{
int data;
struct ThreadNode *lchild,*rchild;
int ltag,rtag;
}ThreadNode,*ThreadTree;
3.2.2 中序线索二叉树

void visit(ThreadNode *q){
if (q->lchild==NULL){
q->lchild=pre;
q->ltag=1;
}
if (pre!=NULL&&pre->rchild==NULL){
pre->rchild=q;
pre->rtag=1;
}
pre=q;
}
void InThread(ThreadTree T){
if (T!=NULL){
InThread(T->lchild);
visit(T);
InThread(T->rchild);
}
}
void CreateInThread(ThreadTree T){
pre=NULL;
if (T!=NULL){
InThread(T);
if (pre->rchild==NULL){
pre->rtag=1;
}
}
}
找后继
在中序线索二叉树中找到指定结点p的中序后继结点next:
ThreadNode *FirstNode(ThreadNode *p){
while (p->ltag==0){
p=p->lchild;
}
return p;
}
ThreadNode *NextNode(ThreadNode *p){
if (p->rtag==0){
return FirstNode (p->rchild);
}else return p->rchild;
}
在中序线索二叉树中找到指定结点p的中序前驱结点pre:
ThreadNode *LastNode(ThreadNode *p){
while (p->rtag==0){
p=p->lchild;
}
return p;
}
ThreadNode *PreNode(ThreadNode *p){
if (p->ltag==0){
return LastNode (p->lchild);
}else return p->lchild;
}
3.2.3 先序线索二叉树


递归算法void visit(ThreadNode *q){
if (q->lchild==NULL){
q->lchild=pre;
q->ltag=1;
}
if (pre!=NULL&&pre->rchild==NULL){
pre->rchild=q;
pre->rtag=1;
}
pre=q;
}
void PreThread(ThreadTree T){
if (T!=NULL){
visit(T);
if (T->ltag==0){
PreThread(T->lchild);
}
PreThread(T->rchild);
}
}
void CreatePreThread(ThreadTree T){
pre=NULL;
if (T!=NULL){
PreThread(T);
if (pre->rchild==NULL){
pre->rtag=1;
}
}
}
找后继
在先序线索二叉树中找到指定结点p的先序后继结点next:
在先序线索二叉树中找到指定结点p的先序前驱结点pre:
①p为左孩子,p的父结点是它的前驱
②p为右孩子且其左兄弟为空,p的父结点为其前驱
③p为右孩子且其左兄弟为空,p的前驱为左兄弟子树中最后一个被先序遍历的结点
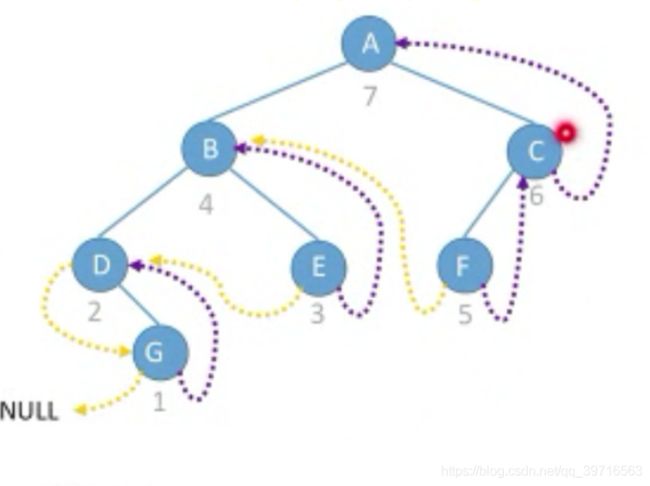
④p是根结点,p没有先序前驱3.2.4 后序线索二叉树

递归算法void visit(ThreadNode *q){
if (q->lchild==NULL){
q->lchild=pre;
q->ltag=1;
}
if (pre!=NULL&&pre->rchild==NULL){
pre->rchild=q;
pre->rtag=1;
}
pre=q;
}
void PostThread(ThreadTree T){
if (T!=NULL){
PostThread(T->lchild);
PostThread(T->rchild);
visit(T);
}
}
void CreatePostThread(ThreadTree T){
pre=NULL;
if (T!=NULL){
PostThread(T);
if (pre->rchild==NULL){
pre->rtag=1;
}
}
}
找后继
在先序线索二叉树中找到指定结点p的先序后继结点next:
①p为右孩子,p的父结点是它的后继
②p为左孩子且其右兄弟为空,p的父结点为其后继
③p为左孩子且其右兄弟为空,p的后继为右兄弟子树中最后一个被后序遍历的结点
④p是根结点,p没有后序前驱
在先序线索二叉树中找到指定结点p的先序前驱结点pre:
①p有右孩子,则p的右孩子为其后序前驱
②p没有右孩子,则p的左孩子为其后序前驱4. 树与森林
4.1 树的存储结构
4.1.1 双亲表示法

优点:查找指定结点的双亲很方便。
缺点:查找指定结点的孩子结点只能从头遍历。#define MAX_TREE_SIZE 100
typedef struct {
int data;
int parent;
}PTNode;
typedef struct {
PTNode nodes[MAX_TREE_SIZE];
int n;
}PTree;
4.1.2 孩子表示法

优点:查找指定结点的孩子很方便。
缺点:查找指定结点的双亲不方便。struct CTNode{
int child;
struct CTNode *next;
};
typedef struct {
int data;
struct CTNode *firstChild;
}CTBox;
typedef struct {
CTBox node [MAX_TREE_SIZE];
int n,r;
}CTree;
4.1.3 孩子兄弟表示法(二叉树表示法)

优点:可以转换为熟悉的二叉树再进行处理
缺点:从已知结点找其双亲结点比较麻烦typedef struct CSNode {
int data ;
struct CSNode *firstchild,*nextsibling;
}CSNode,*CSTree;
4.2 树、森林与二叉树的转化
4.3 树与森林的遍历
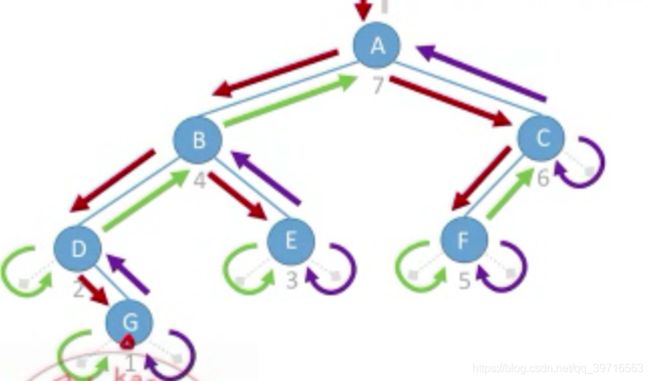
4.3.1 树的先根遍历
4.3.2 树的后根遍历
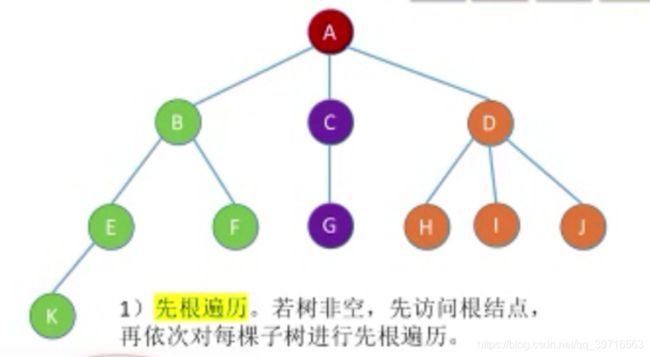
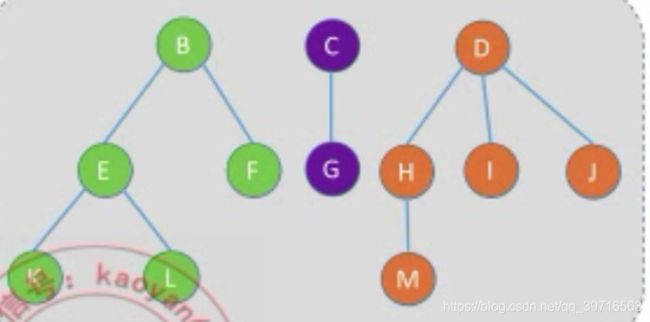
遍历序列:KEFBGCHIJDA4.3.3 树的层次遍历
4.3.4 森林的先序遍历
4.3.4 森林的中序遍历
5. 树与二叉树的应用
5.1 二叉排序树
5.1.1 二叉排序树的定义

对二叉树进行中序遍历可以得到一个递增的有序序列:1、3、4、6、7、8、10、13、145.1.2 二叉排序树的查找
typedef struct BSTNode {
int key;
struct BSTNode *lchild,*rchild;
}BSTNode ,*BSTree;
BSTNode *BST_Search(BSTree T,int key){
while (T!=NULL && key!=T->key){
if (key<T->key){
T=T->lchild;
}else {
T=T->rchild;
}
}
return T;
}
5.1.3 二叉排序树的插入
int BST_Insert(BSTree &T,int k){
if (T==NULL){
T=(BSTree)malloc (sizeof (BSTNode));
T->key=k;
T->lchild=T->rchild=NULL;
return 1;
}
else if (k==T->key)
return 0;
else if (k<T->key)
return BST_Insert(T->lchild,k);
else if (k>T->key)
return BST_Insert(T->rchild,k);
}
5.1.4 二叉排序树的构造
void Creat_BST(BSTree &T,int str[],int n){
T=NULL;
int i=0;
while (i<n){
BST_Insert(T,str[i]);
i++;
}
}
5.1.5 二叉排序树的删除
首先找到目标结点。
5.1.6 查找效率分析

查找成功ASL=(1x1+2x2+4x3+1x4)/8=2.625
查找失败ASL=(3x7+4x2)/9=3.22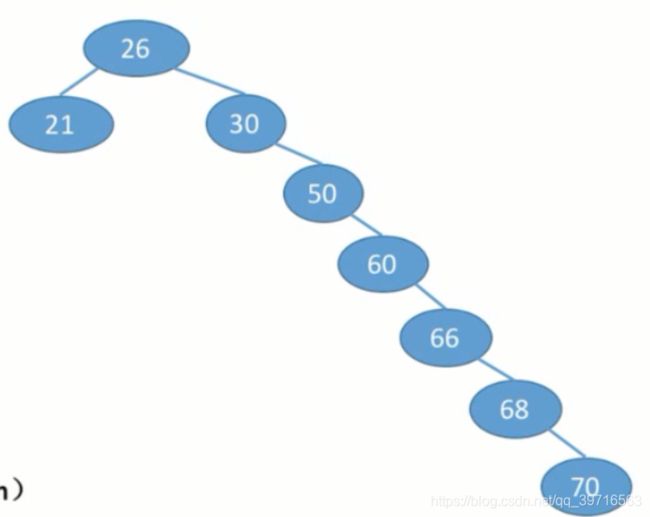
查找成功ASL=(1x1+2x2+3x1+4x1+5x1+6x1+7x1)/8=3.75
查找失败ASL=(2x3+3x4+5x6+7x2)/9=4.22
最坏情况:每个结点只有一个分支,树高h=结点数n,平均查找长度为:O(n
)5.2 平衡二叉树
5.2.1 平衡二叉树的定义
typedef struct AVLNode {
int key;
int balance;
struct AVLNode *lchild,*rchild;
}AVLNode,* AVLTree;
5.2.2 平衡二叉树的插入(旋转)
LL平衡旋转
RR平衡旋转
LR平衡旋转
RL平衡旋转
5.2.3 平衡二叉树的查找
用 n h n_h nh表示深度为h的平衡树中含有的最少的结点数。
当h=0时,0个结点。
当h=1时,1个结点。
当h=2时,2个结点。
当h=3时,4个结点。
可以证明,含有n个结点的平衡二叉树的最大深度为O( l o g 2 n log_2n log2n)
因此平衡二叉树的平均查找长度为O( l o g 2 n log_2n log2n)5.3 哈夫曼树与哈夫曼编码
5.3.1 哈夫曼树的定义
结点的带权路径长度:结点权值 x 树的根结点到该结点的路径长度
树的带权路径长度(WPL):树中所有叶结点的带权路径长度之和。5.3.2 哈夫曼树的构造
5.3.3 哈夫曼编码