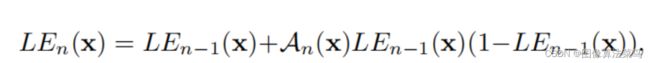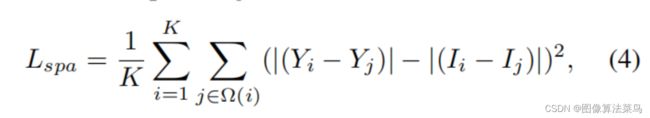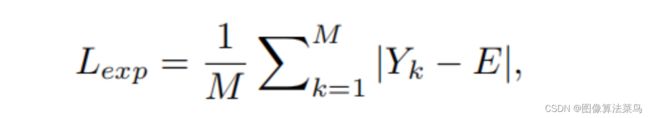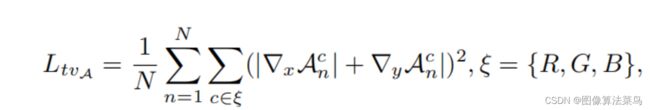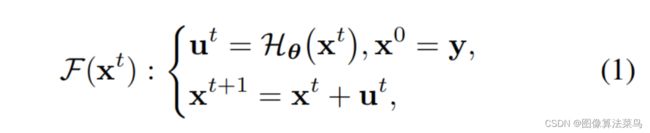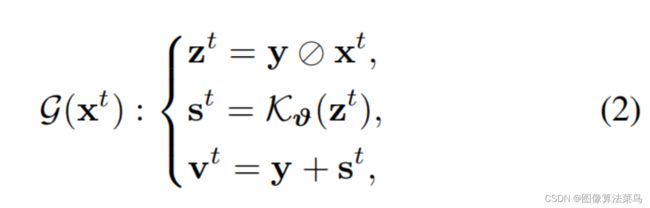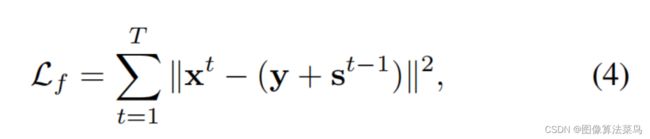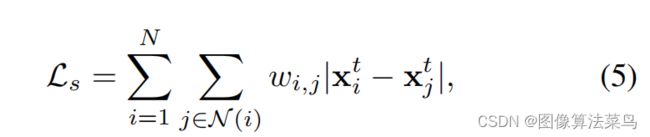无监督低照度图像增强网络ZeroDCE和SCI介绍
目录
简介
Zero-DCE
算法介绍
模型代码
无监督loss介绍
小结
Self-Calibrated Illumination (SCI)
模型介绍
无监督loss介绍
小结
总结
简介
当前有较多深度学习的方法来做图像效果增强,但多数都是有监督的,需要构造成对的数据,实际使用中,获取成对的数据更难。这里分享两篇无监督的图像增强方法,使用了深度学习网络。
Zero-DCE
论文名称:Zero-Reference Deep Curve Estimation for Low-Light Image Enhancement
论文地址:https://openaccess.thecvf.com/content_CVPR_2020/papers/Guo_Zero-Reference_Deep_Curve_Estimation_for_Low-Light_Image_Enhancement_CVPR_2020_paper.pdf
代码地址:GitHub - Li-Chongyi/Zero-DCE: Zero-DCE code and model
算法介绍
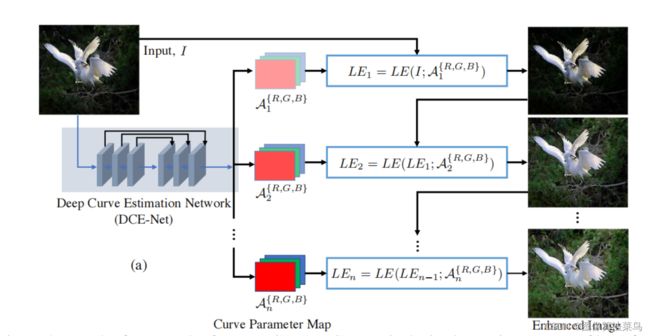
Zero-DCE算法使用了如下公式来做图像增强,通过网络学出An(x),An(x)是和图像分辨率大小一致的,且有RGB三个通道,其中n=8。通过多次迭代来计算出最后的RGB图,其实当图分辨率较大时,计算量是很大的,很耗时的,flops很大,256x256分辨率的图像,flops都超过5G了。
网络本身参数量是比较小的,只是用了7层3x3的卷积网络,中间通道数为32,最后输出24通道的An。
模型代码
模型代码如下
import torch
import torch.nn as nn
import torch.nn.functional as F
import math
#import pytorch_colors as colors
import numpy as np
class enhance_net_nopool(nn.Module):
def __init__(self):
super(enhance_net_nopool, self).__init__()
self.relu = nn.ReLU(inplace=True)
number_f = 32
self.e_conv1 = nn.Conv2d(3,number_f,3,1,1,bias=True)
self.e_conv2 = nn.Conv2d(number_f,number_f,3,1,1,bias=True)
self.e_conv3 = nn.Conv2d(number_f,number_f,3,1,1,bias=True)
self.e_conv4 = nn.Conv2d(number_f,number_f,3,1,1,bias=True)
self.e_conv5 = nn.Conv2d(number_f*2,number_f,3,1,1,bias=True)
self.e_conv6 = nn.Conv2d(number_f*2,number_f,3,1,1,bias=True)
self.e_conv7 = nn.Conv2d(number_f*2,24,3,1,1,bias=True)
self.maxpool = nn.MaxPool2d(2, stride=2, return_indices=False, ceil_mode=False)
self.upsample = nn.UpsamplingBilinear2d(scale_factor=2)
def forward(self, x):
x1 = self.relu(self.e_conv1(x))
# p1 = self.maxpool(x1)
x2 = self.relu(self.e_conv2(x1))
# p2 = self.maxpool(x2)
x3 = self.relu(self.e_conv3(x2))
# p3 = self.maxpool(x3)
x4 = self.relu(self.e_conv4(x3))
x5 = self.relu(self.e_conv5(torch.cat([x3,x4],1)))
# x5 = self.upsample(x5)
x6 = self.relu(self.e_conv6(torch.cat([x2,x5],1)))
x_r = F.tanh(self.e_conv7(torch.cat([x1,x6],1)))
r1,r2,r3,r4,r5,r6,r7,r8 = torch.split(x_r, 3, dim=1)
x = x + r1*(torch.pow(x,2)-x)
x = x + r2*(torch.pow(x,2)-x)
x = x + r3*(torch.pow(x,2)-x)
enhance_image_1 = x + r4*(torch.pow(x,2)-x)
x = enhance_image_1 + r5*(torch.pow(enhance_image_1,2)-enhance_image_1)
x = x + r6*(torch.pow(x,2)-x)
x = x + r7*(torch.pow(x,2)-x)
enhance_image = x + r8*(torch.pow(x,2)-x)
r = torch.cat([r1,r2,r3,r4,r5,r6,r7,r8],1)
return enhance_image_1,enhance_image,r
无监督loss介绍
论文使用了四种loss,Spatial Consistency Loss,主要是保证增强后的图像,空间一致性和原图尽量保持一致。计算4x4邻域里的均值,然后对均值计算邻域梯度,包括上下左右四个方向,尽量保证原图和增强后的图像,这种空间梯度一致性。
Spatial Consistency Loss的代码如下
class L_spa(nn.Module):
def __init__(self):
super(L_spa, self).__init__()
# print(1)kernel = torch.FloatTensor(kernel).unsqueeze(0).unsqueeze(0)
kernel_left = torch.FloatTensor( [[0,0,0],[-1,1,0],[0,0,0]]).cuda().unsqueeze(0).unsqueeze(0)
kernel_right = torch.FloatTensor( [[0,0,0],[0,1,-1],[0,0,0]]).cuda().unsqueeze(0).unsqueeze(0)
kernel_up = torch.FloatTensor( [[0,-1,0],[0,1, 0 ],[0,0,0]]).cuda().unsqueeze(0).unsqueeze(0)
kernel_down = torch.FloatTensor( [[0,0,0],[0,1, 0],[0,-1,0]]).cuda().unsqueeze(0).unsqueeze(0)
self.weight_left = nn.Parameter(data=kernel_left, requires_grad=False)
self.weight_right = nn.Parameter(data=kernel_right, requires_grad=False)
self.weight_up = nn.Parameter(data=kernel_up, requires_grad=False)
self.weight_down = nn.Parameter(data=kernel_down, requires_grad=False)
self.pool = nn.AvgPool2d(4)
def forward(self, org , enhance ):
b,c,h,w = org.shape
org_mean = torch.mean(org,1,keepdim=True)
enhance_mean = torch.mean(enhance,1,keepdim=True)
org_pool = self.pool(org_mean)
enhance_pool = self.pool(enhance_mean)
weight_diff =torch.max(torch.FloatTensor([1]).cuda() + 10000*torch.min(org_pool - torch.FloatTensor([0.3]).cuda(),torch.FloatTensor([0]).cuda()),torch.FloatTensor([0.5]).cuda())
E_1 = torch.mul(torch.sign(enhance_pool - torch.FloatTensor([0.5]).cuda()) ,enhance_pool-org_pool)
D_org_letf = F.conv2d(org_pool , self.weight_left, padding=1)
D_org_right = F.conv2d(org_pool , self.weight_right, padding=1)
D_org_up = F.conv2d(org_pool , self.weight_up, padding=1)
D_org_down = F.conv2d(org_pool , self.weight_down, padding=1)
D_enhance_letf = F.conv2d(enhance_pool , self.weight_left, padding=1)
D_enhance_right = F.conv2d(enhance_pool , self.weight_right, padding=1)
D_enhance_up = F.conv2d(enhance_pool , self.weight_up, padding=1)
D_enhance_down = F.conv2d(enhance_pool , self.weight_down, padding=1)
D_left = torch.pow(D_org_letf - D_enhance_letf,2)
D_right = torch.pow(D_org_right - D_enhance_right,2)
D_up = torch.pow(D_org_up - D_enhance_up,2)
D_down = torch.pow(D_org_down - D_enhance_down,2)
E = (D_left + D_right + D_up +D_down)
# E = 25*(D_left + D_right + D_up +D_down)
return EExposure Control Loss是为了保证图像的亮度在合理的范围,其中E为0.4~0.7,作者验证在这个范围内效果都差异不大,默认为0.6,相关代码如下。
class L_exp(nn.Module):
def __init__(self,patch_size,mean_val):
super(L_exp, self).__init__()
# print(1)
self.pool = nn.AvgPool2d(patch_size)
self.mean_val = mean_val
def forward(self, x ):
b,c,h,w = x.shape
x = torch.mean(x,1,keepdim=True)
mean = self.pool(x)
d = torch.mean(torch.pow(mean- torch.FloatTensor([self.mean_val] ).cuda(),2))
return dColor Constancy Loss是为了保证颜色的准确性,依据是灰度世界,其实也是有些缺陷的,但这个loss对颜色作用还挺大。就是RG的均值尽量相等,RB的均值也尽量相等,GB的均值也尽量相等,代码如下。
class Sa_Loss(nn.Module):
def __init__(self):
super(Sa_Loss, self).__init__()
# print(1)
def forward(self, x ):
# self.grad = np.ones(x.shape,dtype=np.float32)
b,c,h,w = x.shape
# x_de = x.cpu().detach().numpy()
r,g,b = torch.split(x , 1, dim=1)
mean_rgb = torch.mean(x,[2,3],keepdim=True)
mr,mg, mb = torch.split(mean_rgb, 1, dim=1)
Dr = r-mr
Dg = g-mg
Db = b-mb
k =torch.pow( torch.pow(Dr,2) + torch.pow(Db,2) + torch.pow(Dg,2),0.5)
# print(k)
k = torch.mean(k)
return kIllumination Smoothness Loss是为了保证学出来的An具有一定的平滑性,即邻域的梯度尽量小,相关代码如下。
class L_TV(nn.Module):
def __init__(self,TVLoss_weight=1):
super(L_TV,self).__init__()
self.TVLoss_weight = TVLoss_weight
def forward(self,x):
batch_size = x.size()[0]
h_x = x.size()[2]
w_x = x.size()[3]
count_h = (x.size()[2]-1) * x.size()[3]
count_w = x.size()[2] * (x.size()[3] - 1)
h_tv = torch.pow((x[:,:,1:,:]-x[:,:,:h_x-1,:]),2).sum()
w_tv = torch.pow((x[:,:,:,1:]-x[:,:,:,:w_x-1]),2).sum()
return self.TVLoss_weight*2*(h_tv/count_h+w_tv/count_w)/batch_size小结
这篇论文是对低照度图像处理的,没有实际跑过效果,就不对效果进行评价了,从loss来看,这个loss都挺合理的,估计 Exposure Control Loss作用挺大,把图像拉到了亮度适中的范围,主要不足是计算量太大了,在实时性场景基本上没法用。
Self-Calibrated Illumination (SCI)
论文名称:Toward Fast, Flexible, and Robust Low-Light Image Enhancement
论文地址:https://arxiv.org/abs/2204.10137
代码地址:https://github.com/vis-opt-group/SCI
模型介绍
论文是基于Retinex theory,认为只要估计出光照x,即可得到干净真实的图像z,网络参数H就是为了估计光照x的,通过多个模块级联来学出H,可以认为每次学出部分光照,H是权值共享的,但最终是希望一次就准确算出光照x,推理阶段只用到了H,没用到K,且只有一次。增强网络很轻量,只使用了3层3x3的卷积层,不过代码里可以进行扩展为更深一些的网络,不过网络更深,那么计算量也就越大,比较遗憾的是论文没做消融试验来验证为啥使用3层卷积即可。
class EnhanceNetwork(nn.Module):
def __init__(self, layers, channels):
super(EnhanceNetwork, self).__init__()
kernel_size = 3
dilation = 1
padding = int((kernel_size - 1) / 2) * dilation
self.in_conv = nn.Sequential(
nn.Conv2d(in_channels=3, out_channels=channels, kernel_size=kernel_size, stride=1, padding=padding),
nn.ReLU()
)
self.conv = nn.Sequential(
nn.Conv2d(in_channels=channels, out_channels=channels, kernel_size=kernel_size, stride=1, padding=padding),
nn.BatchNorm2d(channels),
nn.ReLU()
)
self.blocks = nn.ModuleList()
for i in range(layers):
self.blocks.append(self.conv)
self.out_conv = nn.Sequential(
nn.Conv2d(in_channels=channels, out_channels=3, kernel_size=3, stride=1, padding=1),
nn.Sigmoid()
)
def forward(self, input):
fea = self.in_conv(input)
for conv in self.blocks:
fea = fea + conv(fea)
fea = self.out_conv(fea)
illu = fea + input
illu = torch.clamp(illu, 0.0001, 1)
return illu自校正模块,只是辅助功能,有利于收敛,如果没有这个参数,估计H很难学,可能容易把H学为0。利用F和G两个网络级联和权值共享,其实级联的次数也不用多,2-3次即可。自校正网络也不大,代码如下。
class CalibrateNetwork(nn.Module):
def __init__(self, layers, channels):
super(CalibrateNetwork, self).__init__()
kernel_size = 3
dilation = 1
padding = int((kernel_size - 1) / 2) * dilation
self.layers = layers
self.in_conv = nn.Sequential(
nn.Conv2d(in_channels=3, out_channels=channels, kernel_size=kernel_size, stride=1, padding=padding),
nn.BatchNorm2d(channels),
nn.ReLU()
)
self.convs = nn.Sequential(
nn.Conv2d(in_channels=channels, out_channels=channels, kernel_size=kernel_size, stride=1, padding=padding),
nn.BatchNorm2d(channels),
nn.ReLU(),
nn.Conv2d(in_channels=channels, out_channels=channels, kernel_size=kernel_size, stride=1, padding=padding),
nn.BatchNorm2d(channels),
nn.ReLU()
)
self.blocks = nn.ModuleList()
for i in range(layers):
self.blocks.append(self.convs)
self.out_conv = nn.Sequential(
nn.Conv2d(in_channels=channels, out_channels=3, kernel_size=3, stride=1, padding=1),
nn.Sigmoid()
)
def forward(self, input):
fea = self.in_conv(input)
for conv in self.blocks:
fea = fea + conv(fea)
fea = self.out_conv(fea)
delta = input - fea
return delta无监督loss介绍
loss上就使用了两种loss,主要是fifidelity loss,另外的smoothing loss只是为了保证空间平滑性。
第一次的F(y)就把光照估计出来,那么第二次光照估计出来的残差就为0,因为此时认为图像中已经没有光照的影响了,已经是干净的图了,估计不出来光照了,这个也是fifidelity loss的来源。总之,就是利用权值共享,不断的来估计光照,但loss上是只有第一次可以估计出光照,后面都估计不出光照了,所以是t>=1之后,光照就估计不出来了。
这个和直方图均衡有点类似的意思,就是如果直方图已经绝对均衡了,再做直方图均衡,效果也不会变了,当然,实际上,直方图不可能做到绝对均衡,所以级联去做直方图均衡效果还是会变换,但也只是振荡。这里也是,loss不可能为0,只是尽可能接近0,也就是希望一次估计出光照,对没有光照的图,就尽量估计不出来光照了。
学出来的效果有点像全局tonemapping的效果,主要是因为网络才3层3x3的卷积,基本上没有局部性,如果网络很深,那么计算量就会暴涨,当然,可以使用类似HDRnet的网络来学x,那样就会有局部性。另外,不知道白天场景效果会如何,是不是白天图像效果不怎样,作者才强调夜景图片。
smooth loss的代码如下,写的有点复杂,没有细致研究了。
class SmoothLoss(nn.Module):
def __init__(self):
super(SmoothLoss, self).__init__()
self.sigma = 10
def rgb2yCbCr(self, input_im):
im_flat = input_im.contiguous().view(-1, 3).float()
mat = torch.Tensor([[0.257, -0.148, 0.439], [0.564, -0.291, -0.368], [0.098, 0.439, -0.071]]).cuda()
bias = torch.Tensor([16.0 / 255.0, 128.0 / 255.0, 128.0 / 255.0]).cuda()
temp = im_flat.mm(mat) + bias
out = temp.view(input_im.shape[0], 3, input_im.shape[2], input_im.shape[3])
return out
# output: output input:input
def forward(self, input, output):
self.output = output
self.input = self.rgb2yCbCr(input)
sigma_color = -1.0 / (2 * self.sigma * self.sigma)
w1 = torch.exp(torch.sum(torch.pow(self.input[:, :, 1:, :] - self.input[:, :, :-1, :], 2), dim=1,
keepdim=True) * sigma_color)
w2 = torch.exp(torch.sum(torch.pow(self.input[:, :, :-1, :] - self.input[:, :, 1:, :], 2), dim=1,
keepdim=True) * sigma_color)
w3 = torch.exp(torch.sum(torch.pow(self.input[:, :, :, 1:] - self.input[:, :, :, :-1], 2), dim=1,
keepdim=True) * sigma_color)
w4 = torch.exp(torch.sum(torch.pow(self.input[:, :, :, :-1] - self.input[:, :, :, 1:], 2), dim=1,
keepdim=True) * sigma_color)
w5 = torch.exp(torch.sum(torch.pow(self.input[:, :, :-1, :-1] - self.input[:, :, 1:, 1:], 2), dim=1,
keepdim=True) * sigma_color)
w6 = torch.exp(torch.sum(torch.pow(self.input[:, :, 1:, 1:] - self.input[:, :, :-1, :-1], 2), dim=1,
keepdim=True) * sigma_color)
w7 = torch.exp(torch.sum(torch.pow(self.input[:, :, 1:, :-1] - self.input[:, :, :-1, 1:], 2), dim=1,
keepdim=True) * sigma_color)
w8 = torch.exp(torch.sum(torch.pow(self.input[:, :, :-1, 1:] - self.input[:, :, 1:, :-1], 2), dim=1,
keepdim=True) * sigma_color)
w9 = torch.exp(torch.sum(torch.pow(self.input[:, :, 2:, :] - self.input[:, :, :-2, :], 2), dim=1,
keepdim=True) * sigma_color)
w10 = torch.exp(torch.sum(torch.pow(self.input[:, :, :-2, :] - self.input[:, :, 2:, :], 2), dim=1,
keepdim=True) * sigma_color)
w11 = torch.exp(torch.sum(torch.pow(self.input[:, :, :, 2:] - self.input[:, :, :, :-2], 2), dim=1,
keepdim=True) * sigma_color)
w12 = torch.exp(torch.sum(torch.pow(self.input[:, :, :, :-2] - self.input[:, :, :, 2:], 2), dim=1,
keepdim=True) * sigma_color)
w13 = torch.exp(torch.sum(torch.pow(self.input[:, :, :-2, :-1] - self.input[:, :, 2:, 1:], 2), dim=1,
keepdim=True) * sigma_color)
w14 = torch.exp(torch.sum(torch.pow(self.input[:, :, 2:, 1:] - self.input[:, :, :-2, :-1], 2), dim=1,
keepdim=True) * sigma_color)
w15 = torch.exp(torch.sum(torch.pow(self.input[:, :, 2:, :-1] - self.input[:, :, :-2, 1:], 2), dim=1,
keepdim=True) * sigma_color)
w16 = torch.exp(torch.sum(torch.pow(self.input[:, :, :-2, 1:] - self.input[:, :, 2:, :-1], 2), dim=1,
keepdim=True) * sigma_color)
w17 = torch.exp(torch.sum(torch.pow(self.input[:, :, :-1, :-2] - self.input[:, :, 1:, 2:], 2), dim=1,
keepdim=True) * sigma_color)
w18 = torch.exp(torch.sum(torch.pow(self.input[:, :, 1:, 2:] - self.input[:, :, :-1, :-2], 2), dim=1,
keepdim=True) * sigma_color)
w19 = torch.exp(torch.sum(torch.pow(self.input[:, :, 1:, :-2] - self.input[:, :, :-1, 2:], 2), dim=1,
keepdim=True) * sigma_color)
w20 = torch.exp(torch.sum(torch.pow(self.input[:, :, :-1, 2:] - self.input[:, :, 1:, :-2], 2), dim=1,
keepdim=True) * sigma_color)
w21 = torch.exp(torch.sum(torch.pow(self.input[:, :, :-2, :-2] - self.input[:, :, 2:, 2:], 2), dim=1,
keepdim=True) * sigma_color)
w22 = torch.exp(torch.sum(torch.pow(self.input[:, :, 2:, 2:] - self.input[:, :, :-2, :-2], 2), dim=1,
keepdim=True) * sigma_color)
w23 = torch.exp(torch.sum(torch.pow(self.input[:, :, 2:, :-2] - self.input[:, :, :-2, 2:], 2), dim=1,
keepdim=True) * sigma_color)
w24 = torch.exp(torch.sum(torch.pow(self.input[:, :, :-2, 2:] - self.input[:, :, 2:, :-2], 2), dim=1,
keepdim=True) * sigma_color)
p = 1.0
pixel_grad1 = w1 * torch.norm((self.output[:, :, 1:, :] - self.output[:, :, :-1, :]), p, dim=1, keepdim=True)
pixel_grad2 = w2 * torch.norm((self.output[:, :, :-1, :] - self.output[:, :, 1:, :]), p, dim=1, keepdim=True)
pixel_grad3 = w3 * torch.norm((self.output[:, :, :, 1:] - self.output[:, :, :, :-1]), p, dim=1, keepdim=True)
pixel_grad4 = w4 * torch.norm((self.output[:, :, :, :-1] - self.output[:, :, :, 1:]), p, dim=1, keepdim=True)
pixel_grad5 = w5 * torch.norm((self.output[:, :, :-1, :-1] - self.output[:, :, 1:, 1:]), p, dim=1, keepdim=True)
pixel_grad6 = w6 * torch.norm((self.output[:, :, 1:, 1:] - self.output[:, :, :-1, :-1]), p, dim=1, keepdim=True)
pixel_grad7 = w7 * torch.norm((self.output[:, :, 1:, :-1] - self.output[:, :, :-1, 1:]), p, dim=1, keepdim=True)
pixel_grad8 = w8 * torch.norm((self.output[:, :, :-1, 1:] - self.output[:, :, 1:, :-1]), p, dim=1, keepdim=True)
pixel_grad9 = w9 * torch.norm((self.output[:, :, 2:, :] - self.output[:, :, :-2, :]), p, dim=1, keepdim=True)
pixel_grad10 = w10 * torch.norm((self.output[:, :, :-2, :] - self.output[:, :, 2:, :]), p, dim=1, keepdim=True)
pixel_grad11 = w11 * torch.norm((self.output[:, :, :, 2:] - self.output[:, :, :, :-2]), p, dim=1, keepdim=True)
pixel_grad12 = w12 * torch.norm((self.output[:, :, :, :-2] - self.output[:, :, :, 2:]), p, dim=1, keepdim=True)
pixel_grad13 = w13 * torch.norm((self.output[:, :, :-2, :-1] - self.output[:, :, 2:, 1:]), p, dim=1, keepdim=True)
pixel_grad14 = w14 * torch.norm((self.output[:, :, 2:, 1:] - self.output[:, :, :-2, :-1]), p, dim=1, keepdim=True)
pixel_grad15 = w15 * torch.norm((self.output[:, :, 2:, :-1] - self.output[:, :, :-2, 1:]), p, dim=1, keepdim=True)
pixel_grad16 = w16 * torch.norm((self.output[:, :, :-2, 1:] - self.output[:, :, 2:, :-1]), p, dim=1, keepdim=True)
pixel_grad17 = w17 * torch.norm((self.output[:, :, :-1, :-2] - self.output[:, :, 1:, 2:]), p, dim=1, keepdim=True)
pixel_grad18 = w18 * torch.norm((self.output[:, :, 1:, 2:] - self.output[:, :, :-1, :-2]), p, dim=1, keepdim=True)
pixel_grad19 = w19 * torch.norm((self.output[:, :, 1:, :-2] - self.output[:, :, :-1, 2:]), p, dim=1, keepdim=True)
pixel_grad20 = w20 * torch.norm((self.output[:, :, :-1, 2:] - self.output[:, :, 1:, :-2]), p, dim=1, keepdim=True)
pixel_grad21 = w21 * torch.norm((self.output[:, :, :-2, :-2] - self.output[:, :, 2:, 2:]), p, dim=1, keepdim=True)
pixel_grad22 = w22 * torch.norm((self.output[:, :, 2:, 2:] - self.output[:, :, :-2, :-2]), p, dim=1, keepdim=True)
pixel_grad23 = w23 * torch.norm((self.output[:, :, 2:, :-2] - self.output[:, :, :-2, 2:]), p, dim=1, keepdim=True)
pixel_grad24 = w24 * torch.norm((self.output[:, :, :-2, 2:] - self.output[:, :, 2:, :-2]), p, dim=1, keepdim=True)
ReguTerm1 = torch.mean(pixel_grad1) \
+ torch.mean(pixel_grad2) \
+ torch.mean(pixel_grad3) \
+ torch.mean(pixel_grad4) \
+ torch.mean(pixel_grad5) \
+ torch.mean(pixel_grad6) \
+ torch.mean(pixel_grad7) \
+ torch.mean(pixel_grad8) \
+ torch.mean(pixel_grad9) \
+ torch.mean(pixel_grad10) \
+ torch.mean(pixel_grad11) \
+ torch.mean(pixel_grad12) \
+ torch.mean(pixel_grad13) \
+ torch.mean(pixel_grad14) \
+ torch.mean(pixel_grad15) \
+ torch.mean(pixel_grad16) \
+ torch.mean(pixel_grad17) \
+ torch.mean(pixel_grad18) \
+ torch.mean(pixel_grad19) \
+ torch.mean(pixel_grad20) \
+ torch.mean(pixel_grad21) \
+ torch.mean(pixel_grad22) \
+ torch.mean(pixel_grad23) \
+ torch.mean(pixel_grad24)
total_term = ReguTerm1
return total_term小结
论文最牛逼的就是无监督,效果还不错,用级联的,权重共享的方式来估计光照,构造loss来做到无监督,无监督的loss的基本假设就是如果已经没有光照的影响了,光照估计就估计不出来光照了,就应该稳定了。从Retinex theory的理论也知道,如果用网络估计出来x,那么干净图z就可以得到,那么确实不需要label,就可以做到无监督。第一级把光照x估计出来了,那么z就得到了,那么再对z进行光照估计(第二级),此时,我们知道z是没有光照的,或者说z的光照x就是1,这时,其实相当于有label了。
总结
无监督是大家追求的目标,这样就不要花大量的财力来造图像label,目前实际使用的多数都是找人来修图,修成某种艺术风格,但这种代价很大。当然,我估计这些无监督的方法,目前也没法用在手机拍照上,效果还是没法保证没问题,一旦出现偏色的场景,大概率就接受不了。但我认为,这些无监督的方法可以用在面向机器的拍照上,作为一些前处理,为后端的机器识别来服务,比如人脸识别,人像分割等等。