Back Propagation 反向传播

3、Back Propagation 反向传播

B站视频教程传送门：PyTorch深度学习实践 - 反向传播

3.1 引出算法

对于简单（单一）的权重 W ，我们可以将它封装到 Neuron（神经元）中，然后对权重W进行更新即可：

但是，往往实际情况中会涉及多个权重（例如下图：会有几十到上百个），我们几乎不可能做到写出所有的解析式：

矩阵论参考：The Matrix Cookbook - http://matrixcookbook.com

所以，引出反向传播（Back Propagation）算法：

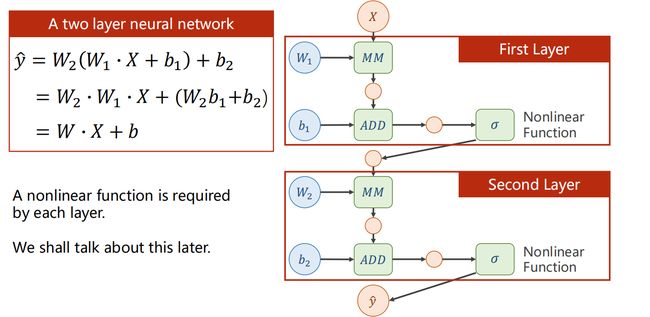
当然，也可以将括号里面展开，如下如所示：

注意：不断地进行线性变化，不管有多少层，最后都会统一成一种形式。

所以：不能够化简（展开），因为增加的这些权重毫无意义。

3.2 非线性函数

所以我们需要引进非线性函数，每一层都需要一个非线性函数！

3.3 算法步骤

在具体讲解反向传播之间，先回顾一下链式求导法则：

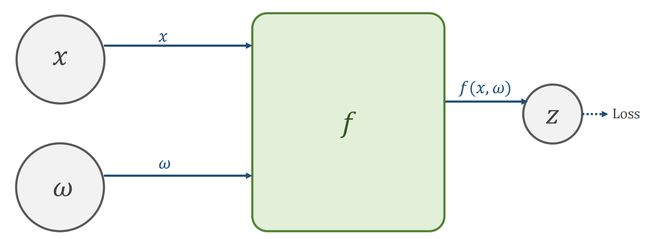
（1）创建计算图表 Create Computational Graph (Forward)

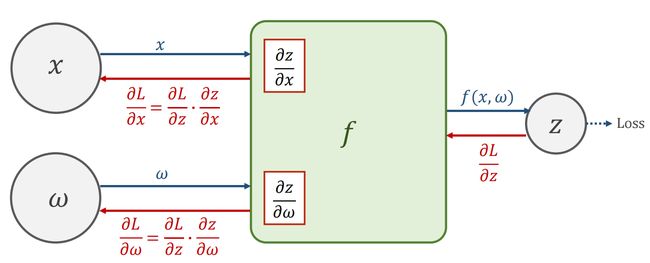
（2）本地梯度 Local Gradient

（3）给出连续节点的梯度 Given gradient from successive node

（4）使用链式规则来计算梯度 Use chain rule to compute the gradient (Backward)

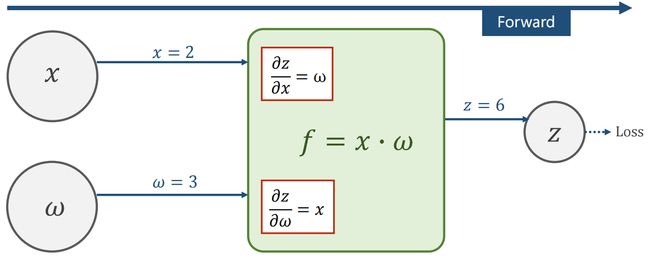
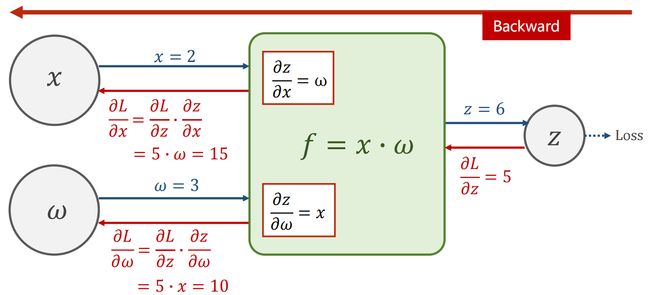
（5）Example: = ∙ , = 2, = 3

3.3.1 例子

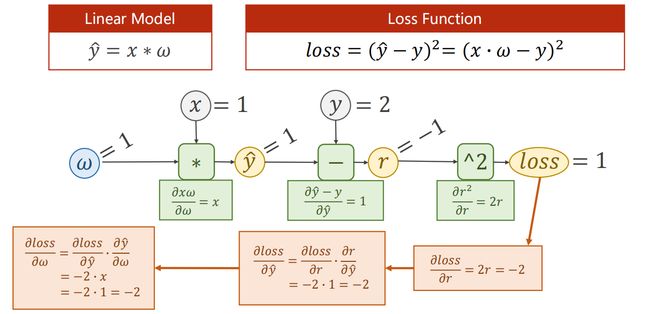
3.3.2 作业1

解答如下：

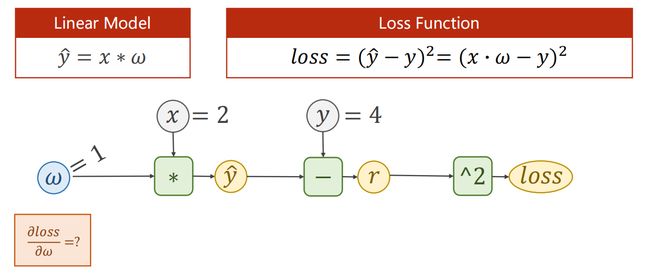
3.3.3 作业2

解答如下：

3.4 Tensor in PyTorch

3.5 PyTorch实现线性模型

import torch

x_data = [1.0, 2.0, 3.0, 4.0]
y_data = [2.0, 4.0, 6.0, 8.0]

w = torch.Tensor([1.0])
w.requires_grad = True  # 计算梯度


def forward(x):
    return x * w


def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y) ** 2


print("predict (before training)", 4, forward(4).item())

for epoch in range(100):
    for x, y in zip(x_data, y_data):
        l = loss(x, y)
        l.backward()
        print('\tgrad:', x, y, w.grad.item())
        w.data -= 0.01 * w.grad.data

        w.grad.data.zero_()

    print("progress:", epoch, l.item())

print("predict (after training)", 4, forward(4).item())

predict (before training) 4 4.0
	grad: 1.0 2.0 -2.0
	grad: 2.0 4.0 -7.840000152587891
	grad: 3.0 6.0 -16.228801727294922
	grad: 4.0 8.0 -23.657981872558594
progress: 0 8.745314598083496
...
	grad: 1.0 2.0 -2.384185791015625e-07
	grad: 2.0 4.0 -9.5367431640625e-07
	grad: 3.0 6.0 -2.86102294921875e-06
	grad: 4.0 8.0 -3.814697265625e-06
progress: 99 2.2737367544323206e-13
predict (after training) 4 7.999999523162842

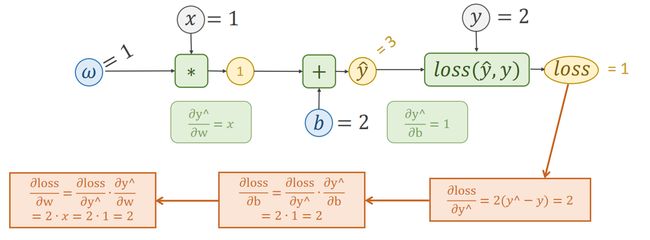
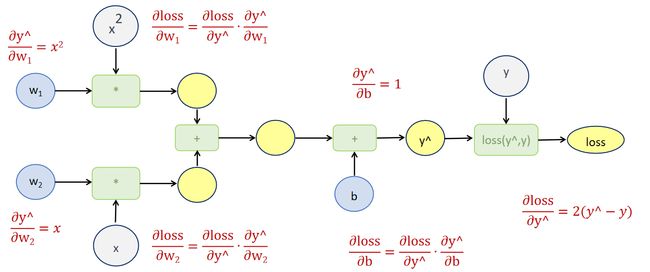
3.6 作业3

解答如下：

代码实现：

import torch

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

w1 = torch.Tensor([1.0])  # 初始权值
w1.requires_grad = True  # 计算梯度，默认是不计算的
w2 = torch.Tensor([1.0])
w2.requires_grad = True
b = torch.Tensor([1.0])
b.requires_grad = True


def forward(x):
    return w1 * x ** 2 + w2 * x + b


def loss(x, y):  # 构建计算图
    y_pred = forward(x)
    return (y_pred - y) ** 2


print('Predict (before training)', 4, forward(4))

for epoch in range(100):
    l = loss(1, 2)  # 为了在for循环之前定义l,以便之后的输出，无实际意义
    for x, y in zip(x_data, y_data):
        l = loss(x, y)
        l.backward()
        print('\tgrad:', x, y, w1.grad.item(), w2.grad.item(), b.grad.item())
        w1.data = w1.data - 0.01 * w1.grad.data  # 注意这里的grad是一个tensor，所以要取他的data
        w2.data = w2.data - 0.01 * w2.grad.data
        b.data = b.data - 0.01 * b.grad.data
        w1.grad.data.zero_()  # 释放之前计算的梯度
        w2.grad.data.zero_()
        b.grad.data.zero_()
    print('Epoch:', epoch, l.item())

print('Predict (after training)', 4, forward(4).item())

Predict (before training) 4 tensor([21.], grad_fn=<AddBackward0>)
	grad: 1.0 2.0 2.0 2.0 2.0
	grad: 2.0 4.0 22.880001068115234 11.440000534057617 5.720000267028809
	grad: 3.0 6.0 77.04720306396484 25.682401657104492 8.560800552368164
Epoch: 0 18.321826934814453
...
	grad: 1.0 2.0 0.31661415100097656 0.31661415100097656 0.31661415100097656
	grad: 2.0 4.0 -1.7297439575195312 -0.8648719787597656 -0.4324359893798828
	grad: 3.0 6.0 1.4307546615600586 0.47691822052001953 0.15897274017333984
Epoch: 99 0.00631808303296566
Predict (after training) 4 8.544171333312988