pytorch 的自动求导机制解释
Ps：在深度理解自动求导机制时，非常幸运一开始看了ronghuaiyang大神翻译的这篇博客https://blog.csdn.net/u011984148/article/details/99670194 从而整体思路没有出现偏差，但是由于本人水平不够的原因好多地方都是懵懵懂懂，一知半解的状态。所以我花了一下午找了相关资料整理了下，将博客理解配上代码重新以更直观的角度理解下这个简单，而又不那么简单的东西。整理框架还是按照上面博客来，细节上进行更简单的阐述。感谢其它参考的文章：https://ptorch.com/news/172.html，https://blog.csdn.net/tsq292978891/article/details/79333707，https://blog.csdn.net/ch1209498273/article/details/79018160，https://blog.csdn.net/ronaldo_hu/article/details/91359018，https://blog.csdn.net/douhaoexia/article/details/78821428（这篇参考帮助理解最多补全了好多细节）。
1.PyTorch基础
PyTorch的版本用的是0.4.0 之后，不考虑之前的版本。废话不多说直接上代码：
import torch
import numpy as np
x = torch.randn(2, 2, requires_grad = True)
print(x.requires_grad)
print('##############')
y = np.array([1., 2., 3.])
y = torch.from_numpy(y)
print(y.requires_grad)
y.requires_grad_(True)
print('after:',y.requires_grad)
True
##############
False
after: True这个例子改成这样就很直观的x定义的是一个x直接定义了一个启用梯度的张量，而y是先定义一个张量，然后用y.requires_grad_(True)来启动张量的梯度功能。
当然 “注意：根据PyTorch的设计，梯度只能计算浮点张量，这就是为什么我创建了一个浮点类型的numpy数组，然后将它设置为启用梯度的PyTorch张量。”这句也copy下。
2.神经网络和反向传播
1、网络进行权值的初始化；
2、输入数据经过卷积层、下采样层、全连接层的向前传播得到输出值；
3、求出网络的输出值与目标值之间的误差也就是损失；
4、反向传播，计算每个权重的梯度
5、根据求得误差进行权值更新。然后在进入到第二步。
损失变化引起的输入权值的微小变化称为该权值的梯度（我们在更新权值时要求的就是这个梯度），并使用反向传播计算。然后使用梯度来更新权值，使用学习率来整体减少损失并训练神经网络。
3.动态计算图
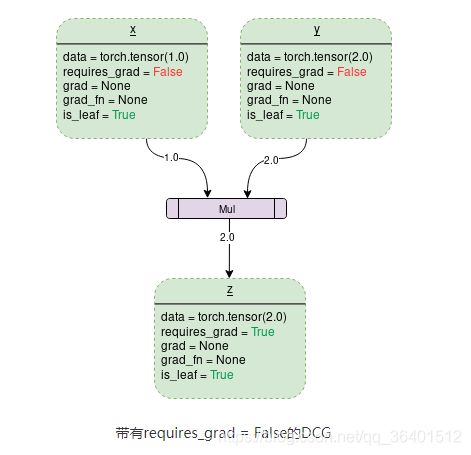
我就贴下copy下这两张图，再用我的话来描述下理解。
首先是两张图的下表的requires_grad=False或者True只是代表张量X的，其次问可以吧X看成是权值W，而Y看成是网络的输入Input，则是输出output。则output=input*W,那么记录的梯度就是
,而W也就是Y为2，那么在X的grad为2.值得注意的是Z的gard_fn为MulBackward，说明是乘法的反向传播求导。
4.Backward()函数
这个是直接用具体例子说明。
import torch
w1 = torch.tensor(2.0,requires_grad=True) #认为w1 与 w2 是函数f1 与 f2的参数
w2 = torch.tensor(2.0,requires_grad=True)
x2 =torch.tensor(3.0,requires_grad=True)
y2 = x2**w1 # f1 运算
z2 = w2*y2+1 # f2 运算
z2.backward()
print(x2.grad)
print(y2.grad)
print(w1.grad)
print(w2.grad)
tensor(12.)
None
tensor(19.7750)
tensor(9.)本来计算4个变量的梯度过程如下：
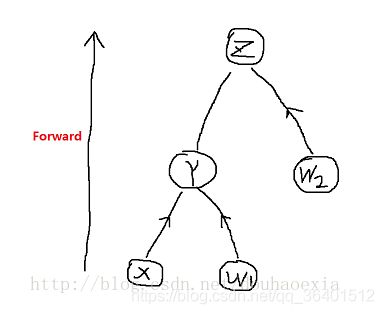
你一定很奇怪明明y2.gard可以计算的，但是显示的是none。其实理解也是相当简单。有博主解释为：发现 x2.grad，w1.grad，w2.grad 是个值 ，但是 y2.grad 却是 None, 说明x2,w1,w2的梯度保留了，y2 的梯度获取不到。实际上，仔细想一想会发现，x2,w1,w2均为叶节点。在这棵计算树中 ，x2 与w1 是同一深度(底层)的叶节点，y2与w2 是同一深度，w2 是单独的叶节点，而y2 是x2 与 w1 的父节点，所以只有y2没有保留梯度值， 印证了之前的说法。同样这也说明，计算图本质就是一个类似二叉树的结构。如下图：
其实更简单的理解你可以认为x是输入z是输出，你反向传播只要知道z对w1和w2的导数即可，根本没必要知道x和y的。
这个一说明然后再次上例子2就好理解一些了
import torch
x = torch.tensor([1.0, 2.0, 8.0], requires_grad=True)
y = torch.tensor([5.0, 1.0, 7.0], requires_grad=True)
z = x * y
z.backward(torch.FloatTensor([1.0, 1.0, 1.0]))
print(y.grad)
tensor([1., 2., 8.])
import torch
x = torch.tensor([1.0, 2.0, 8.0], requires_grad=True)
y = torch.tensor([5.0, 1.0, 7.0], requires_grad=True)
z = x * y
v = torch.tensor( [0.1,1.0,0.001],dtype =torch.float )
z.backward(v)
print(y.grad)
tensor([0.1000, 2.0000, 0.0080])其实我一开始很不理解作者给出的（z.backward() 会给出 RuntimeError: grad can be implicitly created only for scalar outputs）。结合下面换个角度来理解z.backward（v）改放什么。
backward函数是反向传播的入口点，在需要被求导的节点上调用backward函数会计算梯度值到相应的节点上。backward需要一个重要的参数grad_tensor，但如果节点只含有一个标量值，这个参数就可以省略（例如最普遍的loss.backward（）与loss.backward（torch.tensor(1)）等价）
5.数学—雅克比矩阵和向量
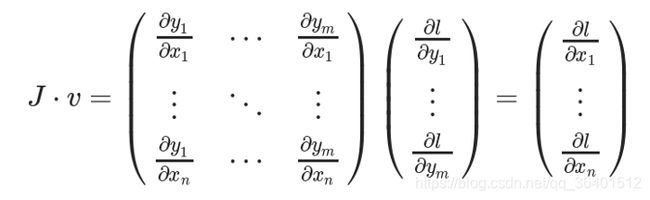
torch.autograd本质上应该是一个向量-雅克比乘积的计算引擎，计算vT⋅J，而所谓的参数
grad_tensor就是这里的v。由定义容易知道，参数grad_tensor需要与Tensor本身有相同的size。通过恰当地设置grad_tensor，容易计算任意的骗到组合。
反向传播的过程一般用来传递上游传来的梯度，从而实现链式法则，简单的推导如下
其中关键是
是什么，其实可以理解为上面的torch.tensor( [0.1,1.0,0.001],dtype =torch.float )实际含义是对比标签的损失。比如Z标签=[5,2,56],Z实际=[5.1,3.0,56.001],那么损失即为 [0.1,1.0,0.001]。那么上个例子中tensor([0.1000, 2.0000, 0.0080])就可以很方便的利用
计算得到。