多传感器融合算法，单目测距、基于双目，长焦短焦，图像拼接，环视等

标定：已知世界坐标系平面内的三维坐标和像素坐标，求解内参和外参；
本质矩阵和基本矩阵：已知内参和两幅图像中对应点的坐标，通过对极约束（八点法，尺度等价性，齐次坐标）求解相机的运动R和t（用到RANSAC）；
单应矩阵：根据同一平面上的点在不同图像上的坐标，得到对应的变换关系（十四讲）；
PNP：根据三维空间点的坐标和他们的投影坐标（归一化平面坐标），估计相机的位姿（用到BA）；
ICP：得到三维点云的变换关系（使用SVD）；

o、基础矩阵及本质矩阵

基础矩阵Fundamental,F是任意两个相机相对关系的内参，换言之，给定了两个相机的相对位置关系和相机内参，F即被确定。
本质矩阵Essential,E是两个标准相机相对关系的内参，换言之，给定两个已标定相机的相对位置关系，E即被确定。

单应性矩阵：

当相机发生纯旋转，或者若场景中的特征点都落在同一平面上（比如墙，地面等）时，计算基础矩阵F或者本质矩阵E往往会有很大的误差(因为此时平移量tt特别小，tt就会特别大)，此时需要用到单应矩阵H。

单应变换也称透视变换或者投影映射，是将图片投影到一个新的视平面，它是二维（x,y）（x,y）到三维(X,Y,Z)(X,Y,Z)，再到另一个二维(x′,y′)(x′,y′)空间的映射．相对于仿射变换，它提供了更大的灵活性，将一个四边形区域映射到另一个四边形区域（不一定是平行四边形）

我们可以从基本矩阵和单应矩阵的推导看到，
// 基本矩阵不依赖于场景中的物体，只和两帧图像间的相对位姿和相机矩阵有关（本质矩阵则与相机矩阵无关）。

// 而单应矩阵不仅仅和帧间的相对位姿有关，还和特定的世界平面有关。

// 所以，当我们得到两帧图像并且知道图像中点的对应关系后，不论场景是什么样的，
// 通过基本矩阵就都已经直接恢复出帧间的运动；
// 而单应矩阵则不行，只有当匹配点都在特定的世界平面中，才可以使用单应来恢复帧间的运动。

一、单目原理

https://zhuanlan.zhihu.com/p/33583981

二、单目测距

https://blog.csdn.net/qq_43010752/article/details/122320949

方法一：自己求焦距，不标定

自己求焦距，不标定：
利用物体实际宽和占用像素求解：

应用：：

F:利用棋盘格进行内参标定;
P:图像中直接获取，
W：利用已知的物体实际距离
例如：一个简单的demo，识别杯子并测距
已知：
杯子宽15 c m 15cm15cm，高9 c m 9cm 9cm
求解发现距离越大误差越大

其他解释：

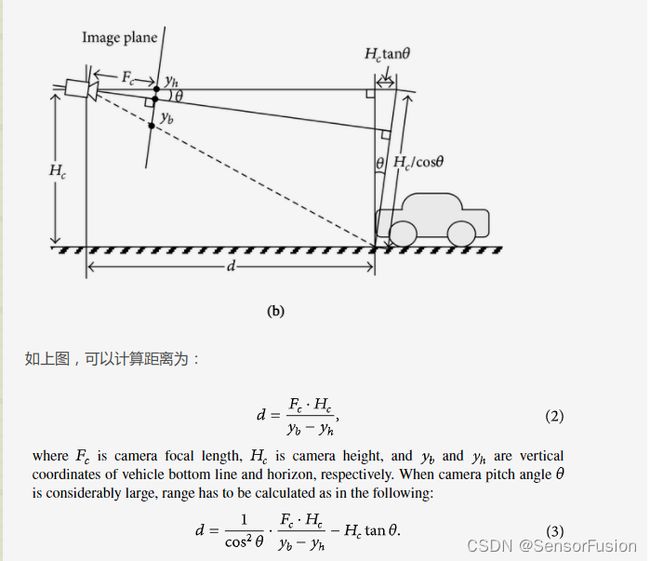
方法二： 相似三角估算

方法三：经典Mobileye

方法四：已知车辆宽度

https://blog.csdn.net/qq_29462849/article/details/120559266

方法五：Apollo基于yolo的方法

1：先检测二维目标，转换为3d图像目标
2：利用图像真实的长宽高还有外参，加上先验的车辆3d图像尺寸及角度，查表对应深度学习，从而求解真实的3d距离信息
https://blog.csdn.net/yuxuan20062007/article/details/83388985

三、双目标定

摄像机标定（包括内参和外参）
双目图像的校正（包括畸变校正和立体校正）
立体匹配算法获取视差图，以及深度图
利用视差图，或者深度图进行虚拟视点的合成

0：左右相机分别进行单目标定，就可以分别得到Rl，Tl，Rr，Tr

1：求解左右相机的RT

因为拍摄了多张图片，利用最小二乘法，也可以是奇异值分解（数学的部分比较复杂，在这里忽略），总而言之，最小化误差，即可得到我们最佳估计的 矩阵，有了这两个矩阵，我们做个旋转、平移就可以了。

个人理解：得到的RT就是左右相机主点，三维坐标的 RT包括旋转，平移，转到内参（根据平移和小孔成像）含有缩放概念

// 如果用matlab标定后：
TranslationOfCamera2：相机2相对于相机1的偏移矩阵，可以直接使用。
RotationOfCamera2：相机2相对于相机1的旋转矩阵，需要转置之后才能使用。

IntrinsicMatrix存放的是摄像头的内参，只与摄像机的内部结构有关，需要先转置再使用。
RadialDistortion：径向畸变，摄像头由于光学透镜的特性使得成像存在着径向畸变，可由K1，K2，K3确定。
TangentialDistortion：切向畸变，由于装配方面的误差，传感器与光学镜头之间并非完全平行，因此成像存在切向畸变，可由两个参数P1，P2确定。
使用时，需要注意参数的排放顺序，即K1，K2，P1，P2，K3。切记不可弄错，否则后续的立体匹配会出现很大的偏差。

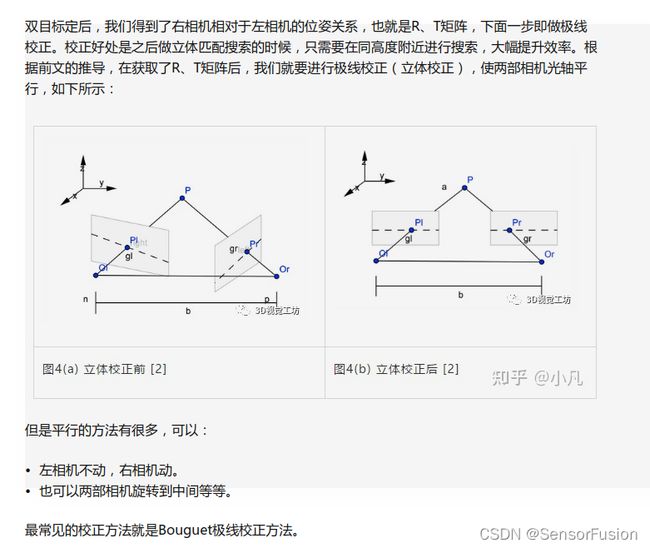
在介绍立体校正的具体方法之前，让我们来看一下，为什么要进行立体校正？

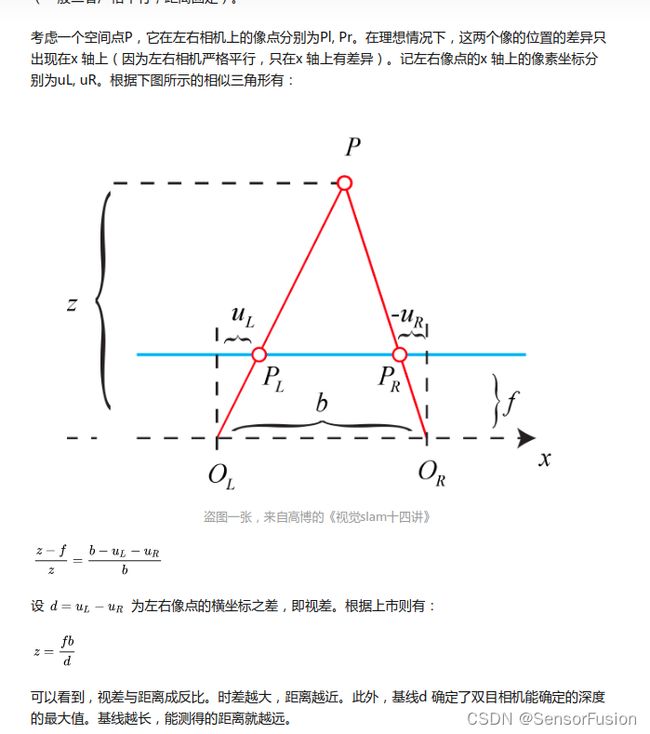
双目摄像机系统主要的任务就是测距，而视差求距离公式是在双目系统处于理想情况下推导的，但是在现实的双目立体视觉系统中，是不存在完全的共面行对准的两个摄像机图像平面的。所以我们要进行立体校正。立体校正的目的就是，把实际中非共面行对准的两幅图像，校正成共面行对准。（共面行对准：两摄像机图像平面在同一平面上，且同一点投影到两个摄像机图像平面时，应该在两个像素坐标系的同一行）,将实际的双目系统校正为理想的双目系统。

理想双目系统：两摄像机图像平面平行，光轴和图像平面垂直，极点处于无线远处，此时点(x0,y0)对应的级线就是y=y0

2：对极约束校正

3：Bouguet校正原理:

完成单目标定，双目外参标定

立体图像校正将图像投影到共同的图像平面上，使得对应的点具有相同的行坐标。
我们完成了校正之后，我们再进行特征点匹配就能将两张图联系到一起，进而求得距离信息。
很多做法中，校正后需要看一下校正的结果，把第一个图像的红通道和第二个图像的蓝通道和绿通道结合构成图像，可以看出浅浅的叠影，红色的就是我们的图1，其他色的就是我们的图2

// matlab 立体矫正
clear all
clc

I1 = imread('zed_left2.png');%读取左右图片
I2 = imread('zed_right2.png');
figure
imshowpair(I1, I2, 'montage');
title('Original Images');

%加载stereoParameters对象。
load('my1stereoParams.mat');%加载你保存的相机标定的mat

[J1, J2] = rectifyStereoImages(I1, I2, stereoParams);
figure
imshowpair(J1, J2, 'montage');
title('Undistorted Images');

双目图像的校正获取对极线校正结果

1. 畸变校正
　　2. 立体校正

双目图像的立体匹配获取视差图

立体校正后的左右两幅图像得到后，匹配点是在同一行上的，可以使用OpenCV中的BM算法或者SGBM算法计算视差图。由于SGBM算法的表现要远远优于BM算法，因此采用SGBM算法获取视差图。SGBM中的参数设置如下：

int numberOfDisparities = ((imgSize.width / 8) + 15) & -16;
    cv::Ptr<cv::StereoSGBM> sgbm = cv::StereoSGBM::create(0, 16, 3);
    sgbm->setPreFilterCap(32);
    int SADWindowSize = 9;
    int sgbmWinSize = SADWindowSize > 0 ? SADWindowSize : 3;
    sgbm->setBlockSize(sgbmWinSize);
    int cn = imgL.channels();
    sgbm->setP1(8 * cn*sgbmWinSize*sgbmWinSize);
    sgbm->setP2(32 * cn*sgbmWinSize*sgbmWinSize);
    sgbm->setMinDisparity(0);
    sgbm->setNumDisparities(numberOfDisparities);
    sgbm->setUniquenessRatio(10);
    sgbm->setSpeckleWindowSize(100);
    sgbm->setSpeckleRange(32);
    sgbm->setDisp12MaxDiff(1);
    int alg = STEREO_SGBM;
    if (alg == STEREO_HH)
        sgbm->setMode(cv::StereoSGBM::MODE_HH);
    else if (alg == STEREO_SGBM)
        sgbm->setMode(cv::StereoSGBM::MODE_SGBM);
    else if (alg == STEREO_3WAY)
        sgbm->setMode(cv::StereoSGBM::MODE_SGBM_3WAY);
    sgbm->compute(imgL, imgR, disp);

计算视差图disparity（matlab）

disparityMap = disparity(rgb2gray(J1), rgb2gray(J2), 'BlockSize',... 
'15',DisparityRange',[0,400],'BlockSize',15,'ContrastThreshold',0.5,'UniquenessThreshold',15);

视差图提取三维深度信息（matlab）

pointCloud3D = reconstructScene(disparityMap, stereoParams);

视差图获取的原理：

void insertDepth32f(cv::Mat& depth)
{
    const int width = depth.cols;
    const int height = depth.rows;
    float* data = (float*)depth.data;
    cv::Mat integralMap = cv::Mat::zeros(height, width, CV_64F);
    cv::Mat ptsMap = cv::Mat::zeros(height, width, CV_32S);
    double* integral = (double*)integralMap.data;
    int* ptsIntegral = (int*)ptsMap.data;
    memset(integral, 0, sizeof(double) * width * height);
    memset(ptsIntegral, 0, sizeof(int) * width * height);
    for (int i = 0; i < height; ++i)
    {
        int id1 = i * width;
        for (int j = 0; j < width; ++j)
        {
            int id2 = id1 + j;
            if (data[id2] > 1e-3)
            {
                integral[id2] = data[id2];
                ptsIntegral[id2] = 1;
            }
        }
    }
    // 积分区间
    for (int i = 0; i < height; ++i)
    {
        int id1 = i * width;
        for (int j = 1; j < width; ++j)
        {
            int id2 = id1 + j;
            integral[id2] += integral[id2 - 1];
            ptsIntegral[id2] += ptsIntegral[id2 - 1];
        }
    }
    for (int i = 1; i < height; ++i)
    {
        int id1 = i * width;
        for (int j = 0; j < width; ++j)
        {
            int id2 = id1 + j;
            integral[id2] += integral[id2 - width];
            ptsIntegral[id2] += ptsIntegral[id2 - width];
        }
    }
    int wnd;
    double dWnd = 2;
    while (dWnd > 1)
    {
        wnd = int(dWnd);
        dWnd /= 2;
        for (int i = 0; i < height; ++i)
        {
            int id1 = i * width;
            for (int j = 0; j < width; ++j)
            {
                int id2 = id1 + j;
                int left = j - wnd - 1;
                int right = j + wnd;
                int top = i - wnd - 1;
                int bot = i + wnd;
                left = max(0, left);
                right = min(right, width - 1);
                top = max(0, top);
                bot = min(bot, height - 1);
                int dx = right - left;
                int dy = (bot - top) * width;
                int idLeftTop = top * width + left;
                int idRightTop = idLeftTop + dx;
                int idLeftBot = idLeftTop + dy;
                int idRightBot = idLeftBot + dx;
                int ptsCnt = ptsIntegral[idRightBot] + ptsIntegral[idLeftTop] - (ptsIntegral[idLeftBot] + ptsIntegral[idRightTop]);
                double sumGray = integral[idRightBot] + integral[idLeftTop] - (integral[idLeftBot] + integral[idRightTop]);
                if (ptsCnt <= 0)
                {
                    continue;
                }
                data[id2] = float(sumGray / ptsCnt);
            }
        }
        int s = wnd / 2 * 2 + 1;
        if (s > 201)
        {
            s = 201;
        }
        cv::GaussianBlur(depth, depth, cv::Size(s, s), s, s);
    }
}

深度图转点云 或者 RGBD 转点云

法一：

#ifndef DEPTH_IMAGE_PROC_DEPTH_CONVERSIONS
#define DEPTH_IMAGE_PROC_DEPTH_CONVERSIONS
 
#include 
#include 
#include 
#include "depth_traits.h"
 
#include 
 
namespace depth_proc {
 
typedef sensor_msgs::PointCloud2 PointCloud;
 
// Handles float or uint16 depths
template<typename T>
void convert(
    const sensor_msgs::ImageConstPtr& depth_msg,
    PointCloud::Ptr& cloud_msg,
    const image_geometry::PinholeCameraModel& model,
    double range_max = 0.0)
{
  // Use correct principal point from calibration
  float center_x = model.cx();//内参矩阵中的图像中心的横坐标u0
  float center_y = model.cy();//内参矩阵中的图像中心的纵坐标v0
 
  // Combine unit conversion (if necessary) with scaling by focal length for computing (X,Y)
  double unit_scaling = DepthTraits<T>::toMeters( T(1) );//如果深度数据是毫米单位的，结果将会为0.001;如果深度数据是米单位的，结果将会为1;
  float constant_x = unit_scaling / model.fx();//内参矩阵中的　f/dx
  float constant_y = unit_scaling / model.fy();//内参矩阵中的　f/dy
  float bad_point = std::numeric_limits<float>::quiet_NaN();
 
  sensor_msgs::PointCloud2Iterator<float> iter_x(*cloud_msg, "x");
  sensor_msgs::PointCloud2Iterator<float> iter_y(*cloud_msg, "y");
  sensor_msgs::PointCloud2Iterator<float> iter_z(*cloud_msg, "z");
  const T* depth_row = reinterpret_cast<const T*>(&depth_msg->data[0]);
  int row_step = depth_msg->step / sizeof(T);
  for (int v = 0; v < (int)cloud_msg->height; ++v, depth_row += row_step)
  {
    for (int u = 0; u < (int)cloud_msg->width; ++u, ++iter_x, ++iter_y, ++iter_z)
    {
      T depth = depth_row[u];
 
      // Missing points denoted by NaNs
      if (!DepthTraits<T>::valid(depth))
      {
        if (range_max != 0.0)
        {
          depth = DepthTraits<T>::fromMeters(range_max);
        }
        else
        {
          *iter_x = *iter_y = *iter_z = bad_point;
          continue;
        }
      }
 
      // Fill in XYZ
      *iter_x = (u - center_x) * depth * constant_x;//这句话计算的原理是什么，通过内外参数矩阵可以计算
      *iter_y = (v - center_y) * depth * constant_y;//这句话计算的原理是什么，通过内外参数矩阵可以计算
      *iter_z = DepthTraits<T>::toMeters(depth);
    }
  }
}
 
} // namespace depth_image_proc
 
#endif

法二：

小孔成像原理：

空间点转像素：

由像素及深度图求点云：




深度图转点云

for (int m = 0; m < depth.rows; m++)
        for (int n=0; n < depth.cols; n++)
        {
            // 获取深度图中(m,n)处的值
            ushort d = depth.ptr<ushort>(m)[n];
            // d 可能没有值，若如此，跳过此点
            if (d == 0)
                continue;
            // d 存在值，则向点云增加一个点
            PointT p;
 
            // 计算这个点的空间坐标
            p.z = double(d) / camera_factor;
            p.x = (n - camera_cx) * p.z / camera_fx;
            p.y = (m - camera_cy) * p.z / camera_fy;
         }

https://blog.csdn.net/BetterEthan/article/details/81812548?utm_source=blogxgwz9

四、RGBD

在这里插入代码片

#ifndef DEPTH_IMAGE_PROC_DEPTH_CONVERSIONS
#define DEPTH_IMAGE_PROC_DEPTH_CONVERSIONS
 
#include 
#include 
#include 
#include "depth_traits.h"
 
#include 
 
namespace depth_proc {
 
typedef sensor_msgs::PointCloud2 PointCloud;
 
// Handles float or uint16 depths
template<typename T>
void convert(
    const sensor_msgs::ImageConstPtr& depth_msg,
    PointCloud::Ptr& cloud_msg,
    const image_geometry::PinholeCameraModel& model,
    double range_max = 0.0)
{
  // Use correct principal point from calibration
  float center_x = model.cx();//内参矩阵中的图像中心的横坐标u0
  float center_y = model.cy();//内参矩阵中的图像中心的纵坐标v0
 
  // Combine unit conversion (if necessary) with scaling by focal length for computing (X,Y)
  double unit_scaling = DepthTraits<T>::toMeters( T(1) );//如果深度数据是毫米单位的，结果将会为0.001;如果深度数据是米单位的，结果将会为1;
  float constant_x = unit_scaling / model.fx();//内参矩阵中的　f/dx
  float constant_y = unit_scaling / model.fy();//内参矩阵中的　f/dy
  float bad_point = std::numeric_limits<float>::quiet_NaN();
 
  sensor_msgs::PointCloud2Iterator<float> iter_x(*cloud_msg, "x");
  sensor_msgs::PointCloud2Iterator<float> iter_y(*cloud_msg, "y");
  sensor_msgs::PointCloud2Iterator<float> iter_z(*cloud_msg, "z");
  const T* depth_row = reinterpret_cast<const T*>(&depth_msg->data[0]);
  int row_step = depth_msg->step / sizeof(T);
  for (int v = 0; v < (int)cloud_msg->height; ++v, depth_row += row_step)
  {
    for (int u = 0; u < (int)cloud_msg->width; ++u, ++iter_x, ++iter_y, ++iter_z)
    {
      T depth = depth_row[u];
 
      // Missing points denoted by NaNs
      if (!DepthTraits<T>::valid(depth))
      {
        if (range_max != 0.0)
        {
          depth = DepthTraits<T>::fromMeters(range_max);
        }
        else
        {
          *iter_x = *iter_y = *iter_z = bad_point;
          continue;
        }
      }
 
      // Fill in XYZ
      *iter_x = (u - center_x) * depth * constant_x;//这句话计算的原理是什么，通过内外参数矩阵可以计算
      *iter_y = (v - center_y) * depth * constant_y;//这句话计算的原理是什么，通过内外参数矩阵可以计算
      *iter_z = DepthTraits<T>::toMeters(depth);
    }
  }
}
 
} // namespace depth_image_proc
 
#endif

五、长焦短焦

1: 利用棋盘格标定

可以代码生产棋盘格

#include 
#include 
#include 

using namespace cv;
using namespace std;

void main()
{
	//---生成标定图
	IplImage    *img;
	int chess_size = 500;
	int dx = 10;    //棋盘格大小，像素为单位
	int dy = 7;     //棋盘格数目
	img = cvCreateImage(cvSize(chess_size*dy, chess_size*dx), IPL_DEPTH_8U, 1);
	cvZero(img);
	int flag = 0;
	for (int i = 0; i < dx; i++)
	for (int j = 0; j < dy; j++)
	{
		flag = (i + j) % 2;
		if (flag == 0)
		{
			for (int m = i*chess_size; m < (i + 1)*chess_size; m++)
			for (int n = j*chess_size; n < (j + 1)*chess_size; n++)
				*(img->imageData + m*img->widthStep + n) = 255;
		}
	}
	cvSaveImage("标定图2.jpg", img);
	// 生成的棋盘格图保存在该工程目录下
	cvNamedWindow("cab", 1);
	cvShowImage("cab", img);
	char ch = cv::waitKey(0);
	if (ch == 27)
	{
		exit(0);
	}
	//system("PAUSE");
	//---END生成标定图
}

在使用opencv中的undistort进行畸变矫正时，需要使用8个参数即fc1, fc2, cc1, cc2, kc1, kc2, kc3, kc4;
RadialDistorion中的参数分别是：kc1,kc2,kc5(不常用)
TangentialDistortion中的参数分别是：kc3,kc4
IntrinsicMatrix中的参数分别是：
fc1 不用 0
不用 fc2 0
cc1 cc2 1
opencv的畸变矫正程序如下：
double fc1, fc2, cc1, cc2, kc1, kc2, kc3, kc4;
fc1 = ;
fc2 = ;
cc1 = ;
cc2 = ;
kc1 = ;
kc2 = ;
kc3 =;
kc4 =;
Mat intrinsic_matrix = (Mat_(3, 3) << fc1, 0, cc1, 0, fc2, cc2, 0, 0, 1);
Mat distortion_coeffs = (Mat_(1, 4) << kc1, kc2, kc3, kc4);

打开stereoCameraCalibrator标定

即可完成内参，左右相机的RT标定，同样可用于长焦短焦的标定

RadialDistortion：径向畸变，来源于光学透镜的特性，由K1，K2，K3确定。
TangentialDistortion：切向畸变，相机装配误差，传感器与光学镜头非完全平行，由两个参数P1，P2确定。
参数排序K1，K2，P1，P2，K3。
这里需要把我们的标定结果保存为mat，方便以后应用
save(‘my1stereoParams.mat’ , ‘stereoParams’);

TranslationOfCamera2：相机2相对于相机1的偏移矩阵，可以直接使用。
RotationOfCamera2：相机2相对于相机1的旋转矩阵，需要转置之后才能使用。

IntrinsicMatrix存放的是摄像头的内参，只与摄像机的内部结构有关，需要先转置再使用。
RadialDistortion：径向畸变，摄像头由于光学透镜的特性使得成像存在着径向畸变，可由K1，K2，K3确定。
TangentialDistortion：切向畸变，由于装配方面的误差，传感器与光学镜头之间并非完全平行，因此成像存在切向畸变，可由两个参数P1，P2确定。
使用时，需要注意参数的排放顺序，即K1，K2，P1，P2，K3。切记不可弄错，否则后续的立体匹配会出现很大的偏差。

2: 利用自然场景特征点

https://www.cnblogs.com/riddick/p/8486223.html

摄像机外参反映的是摄像机坐标系和世界坐标系之间的旋转R和平移T关系。如果两个相机的内参均已知，并且知道各自与世界坐标系之间的R1、T1和R2，T2，就可以算出这两个相机之间的Rotation和Translation，也就找到了从一个相机坐标系到另一个相机坐标系之间的位置转换关系。

// 摄像机外参标定也可以使用标定板，只是保证左、右两个相机同时拍摄同一个标定板的图像。
// 外参一旦标定好，两个相机的结构就要保持固定，否则外参就会发生变化，需要重新进行外参标定。

那么手机怎么保证拍摄同一个标定板图像并能够保持相对位置不变，这个是很难做到的，因为后续用来拍摄实际测试图像时，手机的位置肯定会发生变化。因此我使用外参自标定的方法，在拍摄实际场景的两张图像时，进行摄像机的外参自标定，从而获取当时两个摄像机位置之间的Rotation和Translation。
　　

六、相关基础变换，单应性矩阵及透视变换

https://www.cnblogs.com/vincentcheng/p/7191014.html

#include 
 
#include "highgui.h"
#include "opencv2/imgproc/imgproc.hpp"
 
int main()
{
    // get original image.
    cv::Mat originalImage = cv::imread("road.png");
     
    // perspective image.
    cv::Mat perspectiveImage;
     
    // perspective transform
    cv::Point2f objectivePoints[4], imagePoints[4];
 
    // original image points.
    imagePoints[0].x = 10.0; imagePoints[0].y = 457.0;
    imagePoints[1].x = 395.0; imagePoints[1].y = 291.0;
    imagePoints[2].x = 624.0; imagePoints[2].y = 291.0;
    imagePoints[3].x = 1000.0; imagePoints[3].y = 457.0;
 
    // objective points of perspective image.
    // move up the perspective image : objectivePoints.y - value .
    // move left the perspective image : objectivePoints.x - value.
    double moveValueX = 0.0;
    double moveValueY = 0.0;
 
    objectivePoints[0].x = 46.0 + moveValueX; objectivePoints[0].y = 920.0 + moveValueY;
    objectivePoints[1].x = 46.0 + moveValueX; objectivePoints[1].y = 100.0 + moveValueY;
    objectivePoints[2].x = 600.0 + moveValueX; objectivePoints[2].y = 100.0 + moveValueY;
    objectivePoints[3].x = 600.0 + moveValueX; objectivePoints[3].y = 920.0 + moveValueY;
 
    cv::Mat transform = cv::getPerspectiveTransform(objectivePoints, imagePoints);
 
    // perspective.
    cv::warpPerspective(originalImage,
                        perspectiveImage,
                        transform,
                        cv::Size(originalImage.rows, originalImage.cols),
                        cv::INTER_LINEAR | cv::WARP_INVERSE_MAP);
 
    // cv::imshow("perspective image", perspectiveImage);
    // cvWaitKey(0);
 
    cv::imwrite("perspectiveImage.png", perspectiveImage);
 
    return 0;
}

1：透视变换（Perspective Transformation）

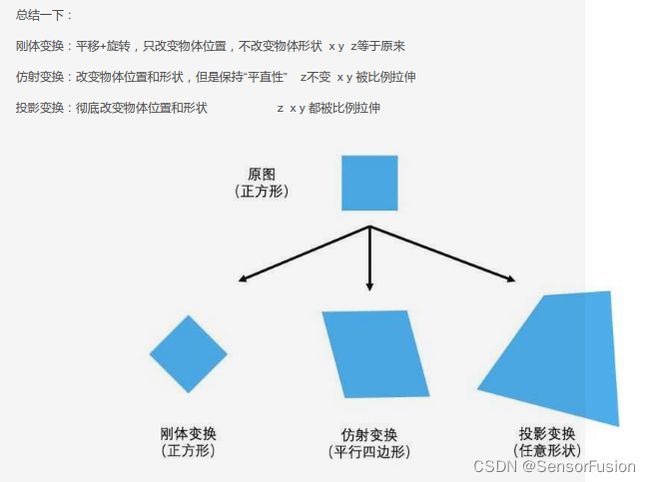
本质是将图像投影到一个新的视平面，其通用变换公式为：

2：仿射变换（Affine Transformation）

可以理解为透视变换的特殊形式。透视变换的数学表达式为：

仿射变换具有两个旋转因子和两个缩放因子，因此具有6个自由度.
不具有保角性和保持距离比的性质，但是原图平行线变换后仍然是平行线.

3：刚体变换

旋转和平移变换/rotation,translation, 3个自由度，点与点之间的距离不变

例如：
激光与单目相机标定，双目与激光标定

https://www.guyuehome.com/11823

七、图像拼接及环视

1：自然场景特征点

要进行图像的无缝拼接，我们的目标就是了获得透视矩阵H，而为了获得透视矩阵，首先需要寻找图像的特征点（sift、surf等等），然后把两个图像中相同的特征点找出来，再根据匹配的特征点计算透视矩阵H。

计算出透视矩阵H之后，剩下的就是把图2经过H矩阵进行透视变换，让图2在图1的坐标系下表示，这时再进行简单的平移拼接即可实现。

那么要实现图像拼接需要那几步呢？简单来说有以下几步：
：对每幅图进行特征点提取
：对对特征点进行匹配
：进行图像配准
：把图像拷贝到另一幅图像的特定位置
：对重叠边界进行特殊处理

2：车载环视场景

为了满足视频拼接的实时性要求，同时考虑到摄像头安装的位置、角度以及不同摄像头之间相互位置相对固定，在本项目中可以使用基于特定图像拼接与查表法相结合的多视点视频拼接方法。

（1）在初始化阶段，首先采集预先放置于车辆前、后、左、右 4个方位的带有棋盘格的标定图像（张正友的方法只考虑了径向畸变，没有考虑切向畸变），利用标定图像分别对4个摄像头进行参数标定，求出并保存每个摄像头图像畸变矫正参数，对标定图像进行畸变矫正，消除摄像头成像失真；

（2）然后对畸变矫正后的标定图像进行射影变换（透视变换），求出并保存射影变换参数；

（3） 接着采集预先放置于车辆前、后、左、右4个方位的带有丰富特征点的特定图像，并通过查找摄像头图像畸变矫正参数进行畸变矫正，通过查找射影变换参数将矫正后的特定图像变换成俯瞰图；

（4） 最后对4个俯瞰图提取 ORB( Oriented FAST and Rotated BRIEF) 特征并进行粗匹配，利用 RANSAC( Random Sample Consensus，随机抽样一致) 算法剔除误匹配点，并拟合出单应性矩阵的初始值，再使用 Levenberg-Marquardt 非线性迭代最小逼近法进行求精，经图像配准、融合和拼接后，生成360°俯瞰全景视图。

（5）在泊车辅助系统启用期间，通过查找已保存的摄像头图像畸变矫正参数、射影变换参数以及单应性矩阵参数，将4个摄像头的视频图像进行拼接，生成虚拟的俯瞰全景视图。

由于摄像头内外参数校正准确性对图像投影效果影响大；需要结合摄像头安装具体情况进行算法的调整；为满足嵌入式系统实时性需求，需要不断优化算法；尽量进行流程简化或者流程自动化。

八、TOF i-tof d-tof

深度图的区别

双目的深度图、RGBD的深度图

目标到相机平面的距离


TOF可能是目标到相机原点距离，具体设备具体分析