PCL点云特征描述与提取
PCL点云特征描述与提取
- 1、局部描述子(local descriptor)
-
- (1)估计某一点的表面法线
- (2)估计一个点云的表面法线
- 2、点特征直方图(Point Feature Histograms)
- 3、快速点特征直方图(FPFH)描述子
- 4、估视点特征直方图(VFH)描述子
1、局部描述子(local descriptor)
在原始表示形式下,点的定义是用笛卡尔坐标系坐标x,y,z相对于一个给定的原点来简单表示的三维映射系统的概念。假定坐标系的原点不随着时间而改变,这里有两个点p1和p2,分别在时间t1和t2捕获,有着相同的坐标。
虽然相对于一些距离测度(如:欧几里得度量)它们是相等的。但是它们取样于完全不同的表面,因此当把它们和邻近的其他环境中的点放在一起时,它们表达着完全不同的信息,这是因为在t1和t2之间局部环境有可能发生改变。
因此作为一个单一实体的三维点概念和笛卡尔坐标系被淘汰了,出现了一个新的概念取而代之:局部描述子(local descriptor)。通过包括周围的邻域,局部描述子能够表征采样表面的几何性质。
相同或相似表面上的点的特征值将非常相似(相对特定度量准则),而不同表面上的点的特征描述子将有明显差异。
(1)刚体变换(rigid transformations)——即三维旋转和三维平移变化不会影响特征向量F估计,即特征向量具有平移旋转不变性;
(2)改变采样密度(varying sampling density)——原则上,一个局部表面小块的采样密度无论是大还是小,都应该有相同的特征向量值,即特征向量具有抗密度干扰性;
(3)噪音(noise)——数据中有轻微噪音的情况下,点特征表示在它的特征向量中必须保持相同或者及其相似的值,即特征向量对点云噪声具有鲁棒性。
PCL中特征向量利用快速kd-tree查询,使用近似法来计算查询点的最近邻元素,有两种常用的查询类型:
(1)决定一个查询点的k邻域元素(k为用户已给参数)(也称为k-搜索);
(2)在半径r的范围内,确定一个查询点的所有邻元素(也称为半径-搜索)。
(1)估计某一点的表面法线
一旦确定邻域以后,查询点的邻域点可用来估计一个局部特征描述子,它用查询点周围邻域点描述采样面的几何特征。
推断它在坐标系中的方位,也就是估计它的法线,表面法线是表面的一个重要属性
(2)估计一个点云的表面法线
表面法线是几何体表面一个十分重要的属性。对于一个已经已经知道的几何体表面,根据垂直于点表面的的矢量,得出表面某一点的法线方向比较容易,然而由于我们获取的点云的数据集在真实的物体的表面表现为一组点的样本,这样就会有两种方法解决:
(1)使用曲面重建技术,从获取的点云数据中得到采样点对应的曲面,然后从曲面模型中计算出表面法线。
(2)直接从点云数据中近似推断表面法线。
在确定表面一点法线的问题近似于估计表面的一个相切面法线的问题,因此转换过来就是求一个最小二乘法平面拟合的问题。
2、点特征直方图(Point Feature Histograms)
点特征表示法只使用很少的几个参数值来近似表示一个点的k邻域的几何特征。然而大部分场景中包含许多特征点,这些特征点有相同的或者非常相近的特征值,因此采用点特征表示法,其直接结果就减少了全局的特征信息。
三维特征描述子中一位成员:点特征直方图(Point Feature Histograms),我们简称为PFH,从PCL实现的角度讨论其实施细节。PFH特征不仅与坐标轴三维数据有关,同时还与表面法线有关。
PFH计算方式通过参数化查询点与邻域点之间的空间差异,并形成一个多维直方图对点的k邻域几何属性进行描述。
它考虑估计法线方向之间所有的相互作用,试图捕获最好的样本表面变化情况,以描述样本的几何特征。因此,合成特征超空间取决于每个点的表面法线估计的质量。最终的PFH描述子通过计算邻域内所有两点之间关系而得到的直方图,因此存在一个O(k) 的计算复杂性。

3、快速点特征直方图(FPFH)描述子
为了简化直方图的特征计算,我们执行以下过程:
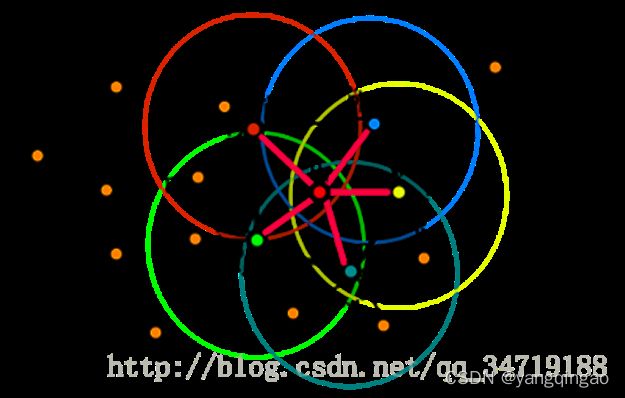
第一步,对于每一个查询点 ,计算这个点和它的邻域点之间的一个元组 (参考上一节PFH的介绍),第一步结果我们称之为简化的点特征直方图SPFH(Simple Point Feature Histograms);
第二步,重新确定每个点的k邻域,使用邻近的SPFH值来计算的最终直方图(称为FPFH)
对于一个已知查询点 ,这个算法首先只利用和它邻域点之间对应关系(上图中以红色线来说明),来估计它的SPFH值,很明显这样比PFH的标准计算少了邻域点之间的互联。
点云数据集中的所有点都要执行这一计算获取SPFH,接下来使用它的邻近点 的SPFH值和点的SPFH值重新权重计算,从而得到点的最终FPFH值
PFH和FPFH的区别:
- FPFH没有对全互连点的所有邻近点的计算参数进行统计,
- PFH特征模型是对查询点周围的一个精确的邻域半径内,而FPFH还包括半径r范围以外的额外点对(不过在2r内);
- 因为重新权重计算的方式,所以FPFH结合SPFH值,重新捕获邻近重要点对的几何信息;
- 由于大大地降低了FPFH的整体复杂性,因此FPFH有可能使用在实时应用中;
4、估视点特征直方图(VFH)描述子
视点特征直方图(VFH)是源于FPFH描述子。由于它的获取速度和识别力,我们决定利用FPFH强大的识别力,但是为了使构造的特征保持缩放不变性的性质同时,还要区分不同的位姿,计算时需要考虑加入视点变量。
我们做了以下两种计算来构造特征,以应用于目标识别问题和位姿估计:
1、扩展FPFH,使其利用整个点云对象来进行计算估计,在计算FPFH时以物体中心点与物体表面其他所有点之间的点对作为计算单元。
2、添加视点方向与每个点估计法线之间额外的统计信息,为了达到这个目的,我们的关键想法是在FPFH计算中将视点方向变量直接融入到相对法线角计算当中。
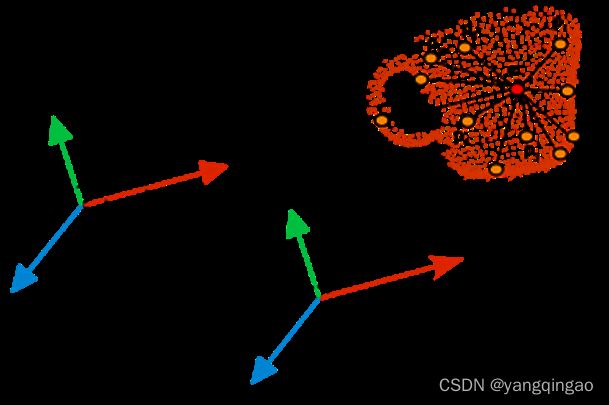
通过统计视点方向与每个法线之间角度的直方图来计算视点相关的特征分量。不是每条法线的视角,因为法线的视角在尺度变换下具有可变性,我们指的是平移视点到查询点后的视点方向和每条法线间的角度。
新组合的特征被称为视点特征直方图(VFH)。下图表体现的就是新特征的想法,包含了以下两部分:
(1)一个视点方向相关的分量
(2)一个包含扩展FPFH的描述表面形状的分量