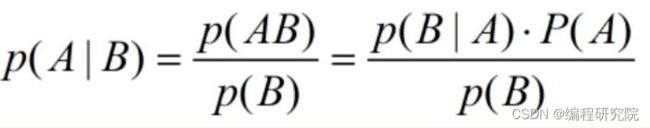算法笔记(7)-朴素贝叶斯算法及Python代码实现
朴素贝叶斯算法有三种类型,分别是贝努利朴素贝叶斯、高斯贝叶斯、多项式朴素贝叶斯。
贝叶斯公式
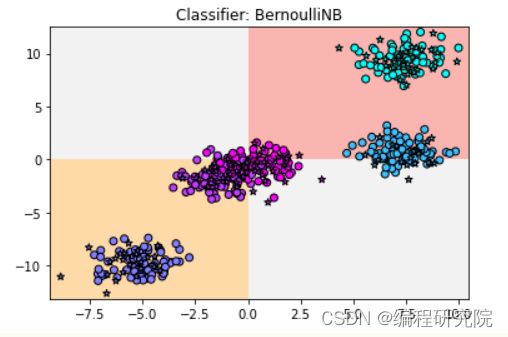
贝努利朴素贝叶斯
适合于符合贝努利分布的数据集,贝努利分布也称为“二项分布”或者是“0-1分布”。
Python代码实现
import matplotlib.pyplot as plt
x_min, x_max = X[:,0].min()-0.5, X[:,0].max()+0.5
y_min, y_max = X[:,1].min()-0.5, X[:,1].max()+0.5
xx,yy = np.meshgrid(np.arange(x_min, x_max,.02),
np.arange(y_min, y_max, .02))
z = nb.predict(np.c_[(xx.ravel(),yy.ravel())]).reshape(xx.shape)
plt.pcolormesh(xx,yy,z,cmap=plt.cm.Pastel1)
plt.scatter(X_train[:,0],X_train[:,1],c=y_train,cmap=plt.cm.cool,edgecolor='k')
plt.scatter(X_test[:,0],X_test[:,1],c=y_test,cmap=plt.cm.cool,marker='*',
edgecolor='k')
plt.xlim(xx.min(),xx.max())
plt.ylim(yy.min(),yy.max())
plt.title('Classifier: BernoulliNB')
plt.show()
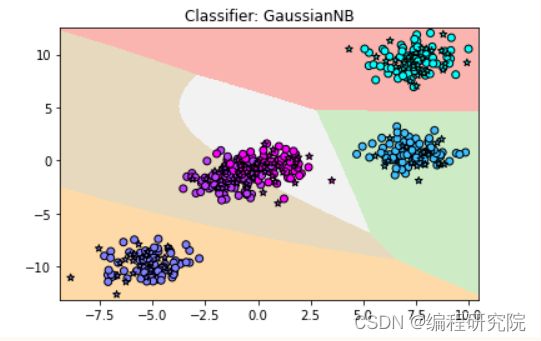
高斯贝叶斯
高斯贝叶斯是假设样本的特征符合高斯分布,或者说符合正态分布时所用的算法。
Python代码实现
z = gnb.predict(np.c_[(xx.ravel(),yy.ravel())]).reshape(xx.shape)
plt.pcolormesh(xx,yy,z,cmap=plt.cm.Pastel1)
plt.scatter(X_train[:,0],X_train[:,1],c=y_train,cmap=plt.cm.cool,edgecolor='k')
plt.scatter(X_test[:,0],X_test[:,1],c=y_test,cmap=plt.cm.cool,marker='*',
edgecolor='k')
plt.xlim(xx.min(),xx.max())
plt.ylim(yy.min(),yy.max())
plt.title('Classifier: GaussianNB')
plt.show()多项式朴素贝叶斯
多项式朴素贝叶斯主要用于拟合多项式分布的数据集,只适合用来对非负离散数值特征进行分类。
Python代码实现
z = mnb.predict(np.c_[(xx.ravel(),yy.ravel())]).reshape(xx.shape)
plt.pcolormesh(xx,yy,z,cmap=plt.cm.Pastel1)
plt.scatter(X_train[:,0],X_train[:,1],c=y_train,cmap=plt.cm.cool,edgecolor='k')
plt.scatter(X_test[:,0],X_test[:,1],c=y_test,cmap=plt.cm.cool,marker='*',
edgecolor='k')
plt.xlim(xx.min(),xx.max())
plt.ylim(yy.min(),yy.max())
plt.title('Classifier: MultinomialNB')
plt.show()由于不让放链接,想要完整代码的朋友,请关注我私信回复“算法笔记7”免费获取