SLAM 07.后端-卡尔曼滤波

 卡尔曼滤波本质上是一个数据融合算法，将具有同样测量目的、来自不同传感器、(可能) 具有不同单位 (unit) 的数据融合在一起，得到一个更精确的目的测量值。
 卡尔曼滤波的局限性在于其只能拟合线性高斯系统，但其最大的优点在于计算量小，能够利用前一时刻的状态（和可能的测量值）来得到当前时刻下的状态的最优估计。

1、应用场合

1、卡尔曼滤波器应用在一些无法直接测量只能间接测量的场合。
2、从一些受误差影响的数据中得到系统状态。

2、两个方程式

运动方程式观测方程。

上图中第一行是运动方程式，第二行是观测方程式。运动方程式中由k-1时刻预测到k时刻的状态。
运动方程式中有状态x^k-1，输入u_k，过程误差w^k(例如风速影响）。
观测方程式中有x^k，观测误差v^k（例如GPS的误差）。

3、状态观测器方程模型

假设我们想知道火箭发动机内部的温度，但是内部温度过高，那么只能通过测量外部温度来间接得到内部温度。
知道燃料的输入W^fuel，知道外部测量输出T_ext,我们想知道发动机内部温度Tⁱⁿ。这个时候我们建立一个数学模型，把上面的输入W^fuel接入，得到输出估计值$\hat{T}$_ext。然后让测量值T_ext和估计值$\hat{T}$_ext之差最小，通过一个增益K反馈到预估模型的输入中，这样就形成了一个模拟反馈系统。如果能得到$\hat{T}$_in，则我们认为这就是近似发动机内部的温度。
如果预估值$\hat{T}$_ext比测量值T_ext越大，则调整反馈让输出的下一个预估值越小。选择上述K的方法就是卡尔曼滤波。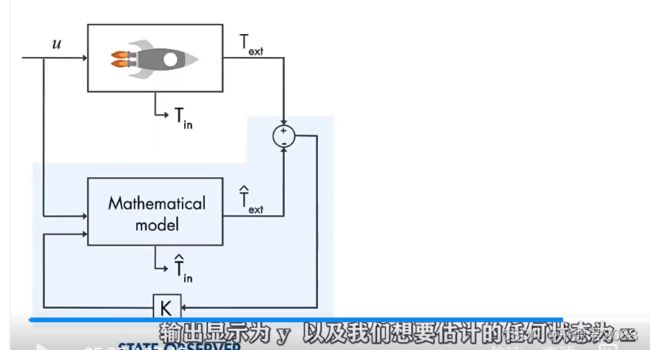
把上面的参数更改为如下：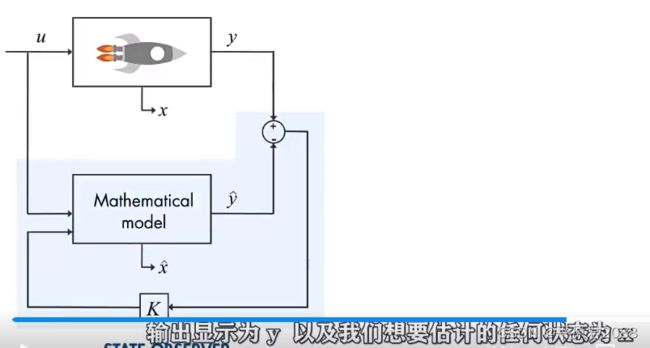
同时我们认为这个模型是线性高斯模型，系统统线性化后如下：

然后进行公式的转换：
上面的解一个指数函数。如果A-KC项小于零，则错误e_abs会随着时间越来越降小，最后$\hat{x}$会收敛到x。
我们要问，是否需要误差反馈项KC呢？即使没有，也会有一个误差衰减的指数函数，但是这里的衰减率仅取决于矩阵A，如果数学模型不确定，则你不知道真实的矩阵A，因此你无法控制误差衰减的速度。给观测器建立反馈回路的重要性在于，使用反馈控制器K可以很好地控制方程，我们可以通过选择相应的控制器增益K来控制误差函数的衰减率，确保更快地消除错误。误差消失地越快，则状态估计$\hat{x}$收敛到真实状态x的速度就越快。选择增益K的最佳方法就是使用卡尔曼滤波器。下面我们将讲解卡尔曼滤波器的原理。

4、卡尔曼滤波器的作用

换一个角度进行解释。

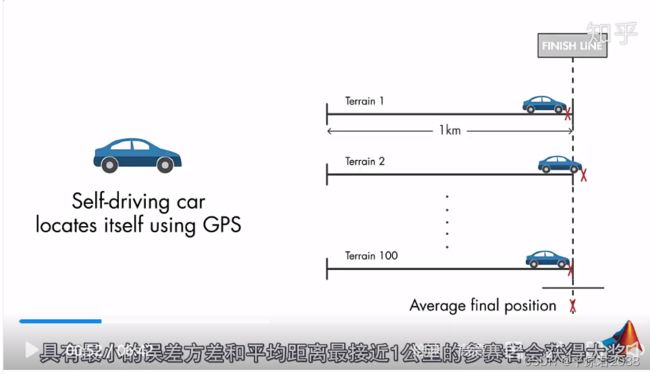
假设参加一个自动驾驶汽车比赛，汽车要在100种不同地形上行驶1公里，比赛结束计算汽车平均的最终位置，只有最小方差并且平均位置最接近1公里终点的团队才能获得大奖。

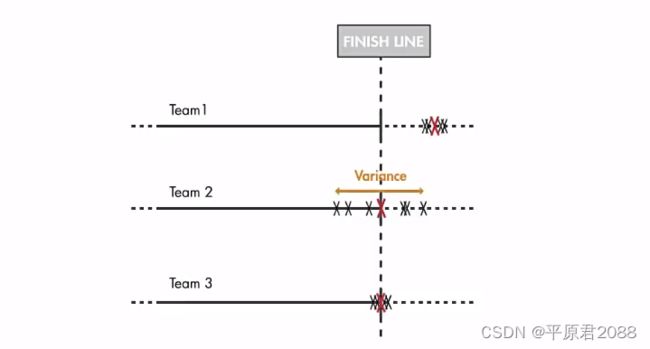
对汽车进行数学建模

输入为速度u_k,系统只有一个状态为汽车的位置x, 上一个位置x_k-1加上速度u_k乘以系数B就是下一个位置。汽车的位置x正是我们要测量的，所以C=1。测量位置y很重要，我们希望位置尽可能靠近终点。但是GPS的读数也有误差，所以我们用一个观测误差v表示，这是一个随机变量。同样也存在过程误差，也是一个随机变量，代表风的影响和汽车速度的变化，我们用w表示。

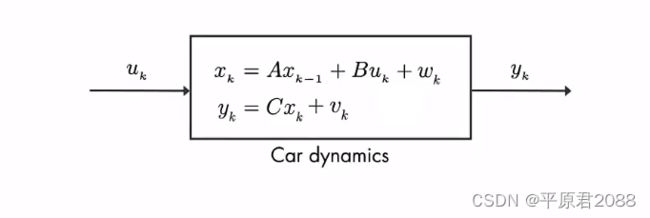
我们认为v和w都是高斯分布，对应的方差分别为R和Q。R的方差是测量误差。

上面就是我们分析出来的汽车的动力学模型。但是实际上我们现实中汽车只是一个黑匣子，我们只是测量出的汽车位置y，为此要单独建立一个汽车模型，这个汽车模型就是经过对动力学模型分析后的抽象化。

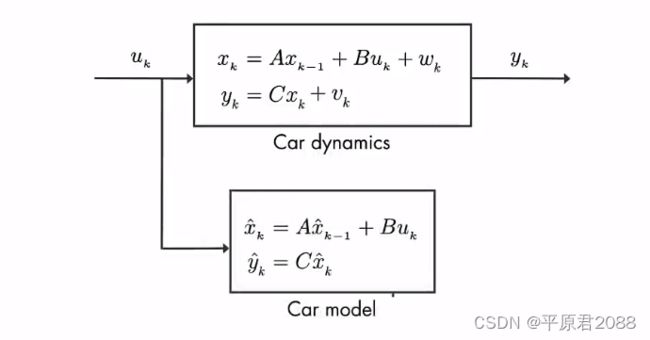
有了这个汽车模型，我们可以对输入进行运算来预估汽车的位置。输入还是速度u_k，位置$\hat{x}$_k-1从初始开始计算，然后叠加速度u_k得到下一个位置$\hat{x}$_k，接着乘以C计算出预估的位置$\hat{y}$_k。

但是这里的预估位置$\hat{y}$_k也是存在误差不准确的，所以需要测量值y_k来矫正，但是因为存在过程误差，所以y_k也是不确定的。这时就是卡尔曼滤波发挥作用的地方。
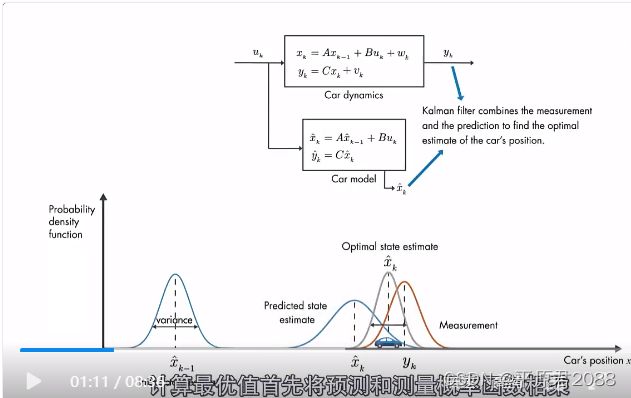
卡尔曼滤波结合测量值y_k和预估值$\hat{y}$_k得到汽车位置的最优估计。

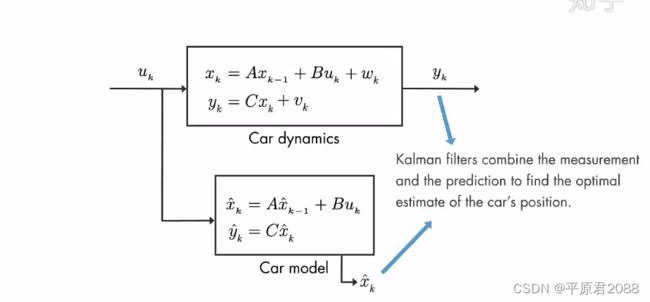
我们将借助概率密度函数直观地讨论卡尔曼滤波的工作原理。

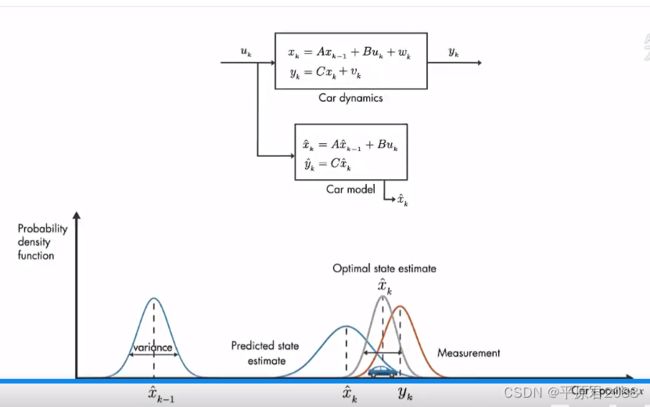
预估模型预测汽车的位置，存在不确定性以概率密度函数来表示（图中蓝线），表示为高斯分布。汽车位置最有可能在这个分布的平均值周围，误差以方差表示。在k-1时刻方差比较小，运行了一段时间在下一时刻k误差增大，在这里以较大的方差表示。同时还存在观测位置y_k也存在观测偏差，也是高斯分布（图中橙色线）。我们现在有了预测和测量，那么对汽车位置的最佳估计是什么？
事实证明，对汽车位置的最佳估计是把两者结合起来。最佳估计就是将预测更新和测量更新所得的数据融合起来，得到一个新的估计。而这个融合，就是一个简单的“乘法”，并利用了一个性质：两个高斯分布的乘积仍然是高斯分布。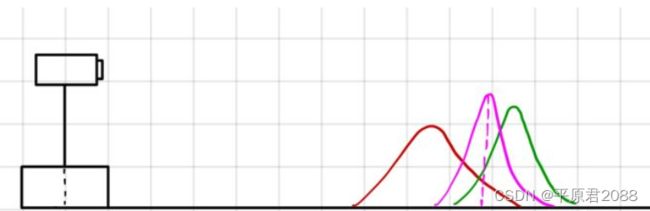
具体就是两个概率函数相乘，得到的结果也是高斯函数，该概率函数的方差比他们更小，该概率函数的平均位置为我们提供了汽车位置的最佳估计，这就是卡尔曼滤波背后的基本思想。实际上就是通过测量值对预估值进行矫正得到最优预估值，这点和最小二乘法回归有点类似。

5、卡尔曼滤波器的原理

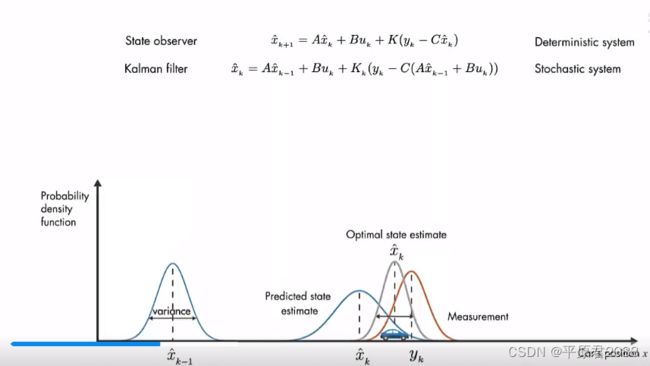
卡尔曼滤波器其实就是前面所讲的一种状态观测器，但他是为随机系统设计的。

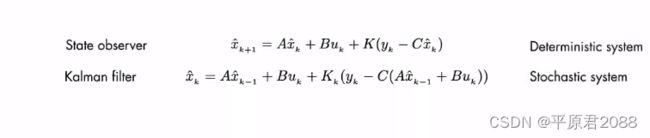
变换为如下：

A$\hat{x}$_k-1+Bu_k 合并为一项为 $\hat{x}$_k^-,把这项叫做预估值，她是在测量之前计算的。然后把上述等式重写为如下：
等式用测量值y_k代入来更新预估值，我们把结果$\hat{x}$_k叫做后验估计。

卡尔曼滤波分第一步：先得到预估值；第二步：把观测值带入更新得到后验值。
具体如下，这就是需要在汽车的ECU(电子控制单元或者行车电脑)上运行的公式：
上图中R为测量概率密度函数，代表着过程误差（例如风速的影响）。
Q为观测误差，例如GPS的误差。R和Q都是高斯分布，前面讲过。

第一步：计算状态预估值$\hat{x}$_k^-,和误差协方差P_k^-。
在单状态系统中P是状态预估值的方差，它作为状态不确定的度量。这种不确定性来自于过程误差和预估值$\hat{x}$_k-1的不确定的影响。
最初的$\hat{x}$_k-1和P_k-1来自于初始估计值。

第二步：把第一步得到的预估值$\hat{x}$_k^-和测量值代入右边的公式进行更新并得到新的预估值$\hat{x}$_k，这个作为下一个时刻代入左边公式进行迭代。

所以卡尔曼滤波器就是 不断的迭代过程，并且只和上一个时刻有关。

在右侧公式中，需要知道卡尔曼增益K,而K的计算需要依赖上一个时刻的预估概率密度P_k^-以及过程误差R。所以这也是需要计算P_k^-的原因。 但是计算P_k^-需要前一个时刻的P_k-1，实际就是右边公式中的P_k。这样就是左右两个公式不断迭代。

卡尔曼增益K用来调节测量值y和预估值对下一刻预估值的影响比例。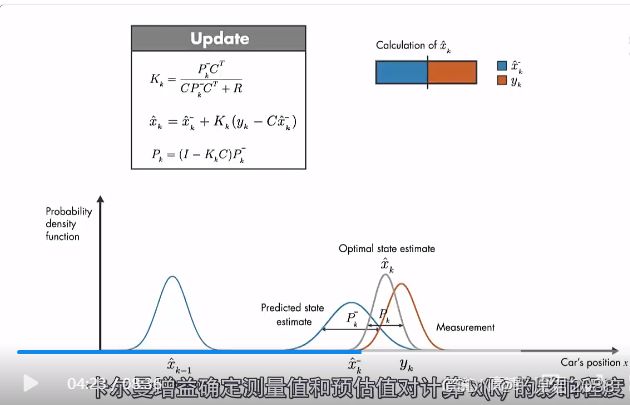如果测量误差误差小，则测量结果y的贡献大。如果预估值的误差小，则预估值对下一个时刻的预估状态贡献大。这样最终的预估值结果就是前一个时刻的预估值和当前测量值的综合，具体表现就是如下图中间那个介于两者之间灰色的高斯分布。该概率的分布方差更小，均值位于两者之间，是一个最优预估。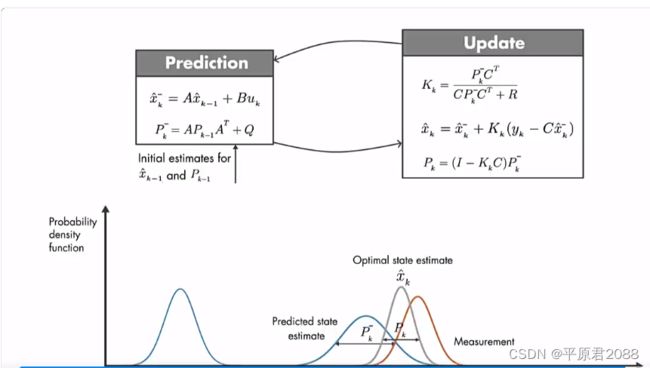
可以举极端情况来说明，假设测量协方差R为0，则预估值就是只有测量值y做出贡献。

反过来如果预估协方差P为0，则最优预估的贡献只来自于预估值。

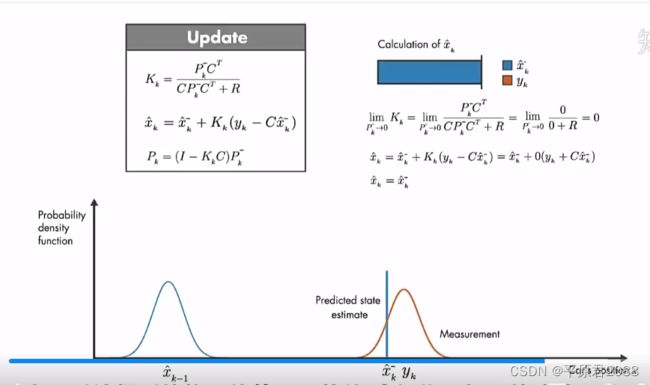
所以这个卡尔曼滤波的增益K设置得相当巧妙，它用来调节预估值和当前测量值对于最优估计的贡献的权重。并且和两者对应的误差方差相关：那个方差越小（误差越小）则那个贡献越大。这样就让最优估计更靠谱。
这样你在上述汽车比赛中，就可在ECU(行车电脑)中运行一个预估模型，然后根据上面的公式把得到的测量值y不断进行更新，同时计算预估值和测量值的概率密度，不断迭代，得到下一个时刻的最优位置预估，从而控制车辆的速度和位置。
上面实际是自己设计一个预估数学模型，然后和测量值y结合，使用卡尔曼滤波得到最优估计。当然了卡尔曼滤波可以看做是多传感器融合的一种算法。你可以增加额外的传感器IMU,来通过多个传感器的你的自动驾驶对位置估算的精度。如下图橙色所示。

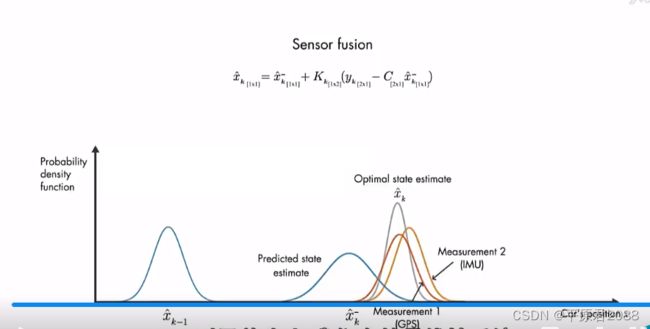
这时就存在多个y,计算方法还是和前面一样，最后结果就是把预估模型和几个测量方差概率密度函数相乘，得到最优预估。
当然我们上面讲的只是线性系统，但是现实中大量存在非线性的系统，这时如果想用卡尔曼滤波器该如何处理呢？下面将进行讲解。

6、非线性状态估计器

6.1、扩展卡尔曼滤波（EKF)

前面的卡尔曼滤波适用于线性系统。但是大量的系统是非线性的，这里这里用过程函数f()和观测函数g()来表示，进行非线性化。当然了观测误差和预估误差这里表示为线性叠加方式，但是很多也是非线性叠加的。
高斯分布经过线性变换后还是高斯分布。

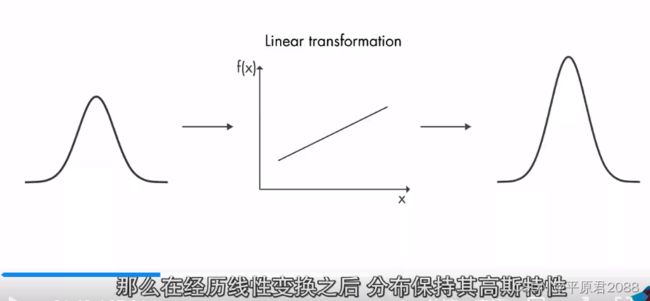
但是高斯分布经过非线性系统变换后就不是高斯分布了。

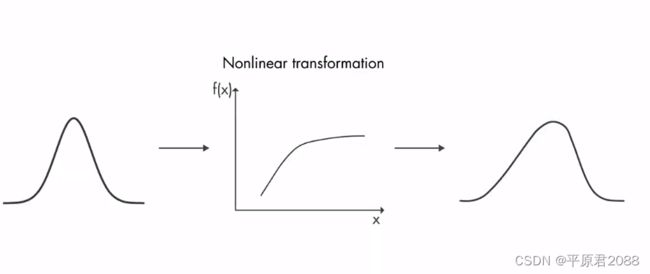
扩展卡尔曼滤波就是把非线性函数在当前原状态的平均值附近进行线性化。

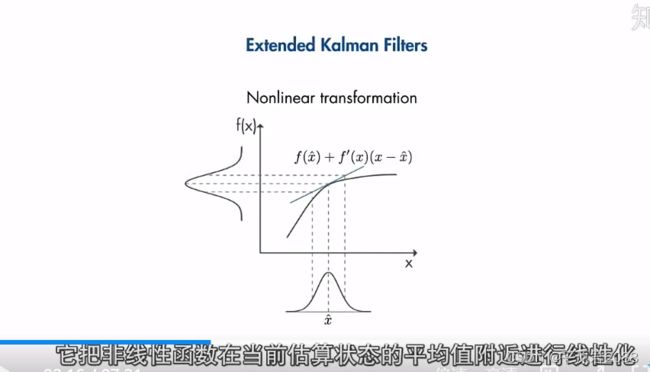
在每个时间步执行线性化，然后将得到的雅克比矩阵用于预测和更新卡尔曼滤波器算法的状态。

下面是按照高翔博士讲的内容，对扩展卡尔曼滤波重新讲解一遍。
卡尔曼滤波实际是把运动时候的内部传感器（例如里程计数器）和外部观测传感器（例如GPS）的融合。需要注意的是，卡尔曼滤波仅适用于线性系统。当系统是非线性，但是可以用线性近似的时候，就可以用扩展卡尔曼滤波了。
如果果将高斯分布作为输入，输入到一个非线性函数中，得到的结果将不再符合高斯分布，也就将导致卡尔曼滤波器的公式不再适用。但是我们进行了一阶线性近似，所以就考虑假设变换后的随机变量仍旧是正态分布。因此我们需要将上面的非线性函数转化为近似的线性函数求解。
我们已经知道非线性滤波主要体现在运动模型以及观测模型都是非线性的，比如：
u^k是输入量，w^k是噪声，y_j是路标（3D点），v^k是观测噪声，z_k,j是像素(例如相机的2D图像)。
如果没有运动方程，只有观测数据，则是纯粹视觉的SLAM,例如没有IMU、GPS等。
然后把路标y和x合并,则方程式简化如下：


区别就是在工作点附近的一阶泰勒展开，得到是的雅克比矩阵。


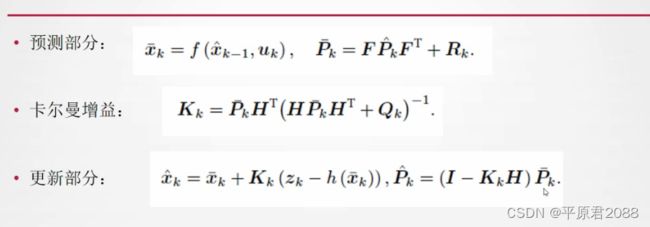
但是EKF有如下缺点：

• 由于复杂的倒数，很难计算出雅克比矩阵。
• 如果雅克比矩阵是数值方式则计算量很大。
• 扩展卡尔曼只适用于可微分练习的模型，因为系统不可微分时候雅克比矩阵不存在。
• 如果系统是高度非线性的则扩展卡尔曼滤波不是最优方法，如下图：
  

6.2、无迹卡尔曼滤波（UKF)

可以用UKF（无迹卡尔曼滤波器）解决上面扩展卡尔曼滤波的问题。

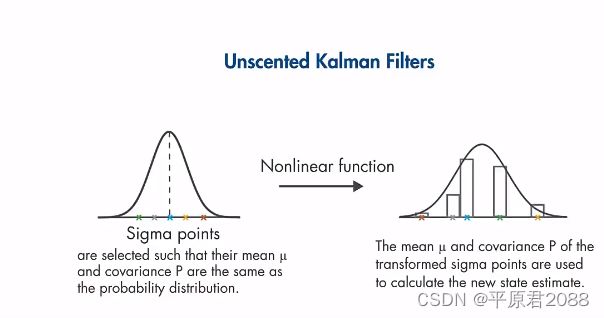
UKF不像EKF那样近似非线性函数，而是近似概率分布。
UKF通过选择一组最小的采样点，让他们的均值和协方差与该概率分布相同。这些点叫西格玛点，围绕着均值对称分布。然后每个西格玛点通过非线性模型计算，并计算非线性变换后输出点的均值和方差，计算经验高斯分布，用来计算新的状态。
在卡尔曼滤波中使用状态转移函数计算误差协方差P，然后用测量值进行更新。然而在UKF中不使用此方法，而是以经验值获取。

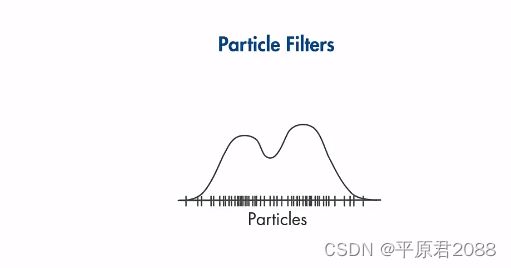
6.3、粒子滤波器(PF)

它使用的样本采样点称为粒子，采样点可以随意分布。和UKF的显著区别是粒子滤波器可以任意分布，不限于高斯分布假设。为了表示任意分布，所需要的粒子数目要远多于UKF的粒子数。

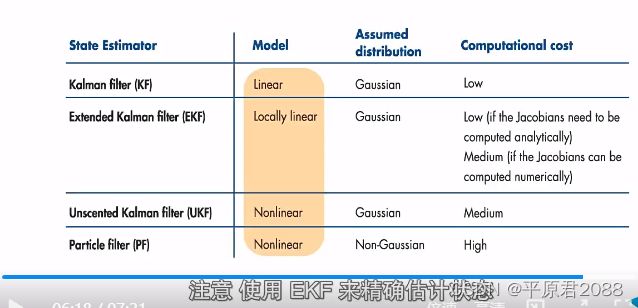
7、比较

8、总结

参考

卡尔曼滤波：从入门到精通
如何通俗并尽可能详细地解释卡尔曼滤波？