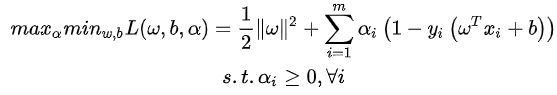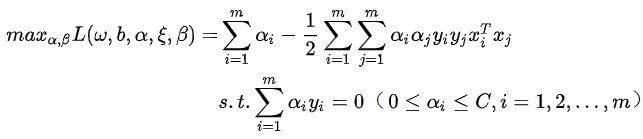机器学习面试

评估指标

分类问题：

准确率 - accuracy、精确率 - precision、召回率 - recall、F1值 - F1-score、ROC曲线下面积 - ROC-AUC （area under curve）、PR曲线下面积 - PR-AUC

回归问题：MAE、MSE、RMSE

优化方法

梯度下降、批梯度下降、随机梯度下降、

momentum、Adagrade、RMSProp、Adam

激活函数

sigmoid和softmax、tanh、Relu和Leaky Relu

损失函数

分类损失：

0-1损失、交叉熵损失(log对数损失)、合页损失

回归损失：

平均绝对值误差-MAE(L1损失)、均方误差-MSE(L2损失)、Huber 损失

过/欠拟合问题

过拟合：增加数据、正则化、Dropout、BN

欠拟合：

样本不平衡

欠采样/过采样、树模型、阈值调整、适合的评价指标

特征选择方法

过滤方法：覆盖率、皮尔森相关系数

嵌入方法：正则化项、输出特征重要性权重

梯度消失/梯度爆炸

本质上是因为神经网络的更新方法，梯度消失是因为反向传播过程中对梯度的求解会产生sigmoid导数和参数的连乘，sigmoid导数的最大值为0.25，权重一般初始都在0，1之间，乘积小于1，多层的话就会有多个小于1的值连乘，导致靠近输入层的梯度几乎为0，得不到更新。梯度爆炸是也是同样的原因，只是如果初始权重大于1，或者更大一些，多个大于1的值连乘，将会很大或溢出，导致梯度更新过大，模型无法收敛。

从反向传播推导到梯度消失and爆炸的原因及解决方案（从DNN到RNN，内附详细反向传播公式推导） - 知乎引言：参加了一家公司的面试和另一家公司的笔试，都问到了这个题！看来很有必要好好准备一下，自己动手推了公式，果然理解更深入了！持续准备面试中。。。 一. 概述：想要真正了解梯度爆炸和消失问题，必须手推反…https://zhuanlan.zhihu.com/p/76772734

梳理常见机器学习面试题 - 知乎16薪的京东零售 算法岗 2022届校招提前批和实习生招聘！！！招聘内推码：C50N 或者发我邮箱：[email protected] 姓名+手机号+邮箱部门直推、直接面试 免笔试 免笔试 免笔试岗位信息：算法工程师、NLP 算法工程师、…https://zhuanlan.zhihu.com/p/82105066

---

模型

LR推导

---

SVM推导

SVM 是一种二类分类模型，它的基本思想是在特征空间中寻找间隔最大的分离超平面。有三种情况：

• 当训练样本线性可分时，通过硬间隔最大化，学习一个线性分类器，即线性可分支持向量机；
• 当训练数据近似线性可分时，引入松弛变量，通过软间隔最大化，学习一个线性分类器，即线性支持向量机；
• 当训练数据线性不可分时，通过使用核技巧及软间隔最大化，学习非线性支持向量机。

目标函数 (硬间隔)：

求解目标函数 (硬间隔)：

用拉格朗日函数，将不等式约束融入目标函数中。

 满足KKT条件，转换成对偶问题。

 先求内部最小值，对 w 和 b 求偏导并令其等于 0 可得：

 将其代入到上式中去可得到：

 此时需要求解  ，利用SMO（序列最小优化）算法：

SMO算法的基本思路是每次选择两个变量  和 ，选取的两个变量所对应的样本之间间隔要尽可能大，因为这样更新会带给目标函数值更大的变化。SMO算法之所以高效，是因为仅优化两个参数的过程实际上仅有一个约束条件，其中一个可由另一个表示，这样的二次规划问题具有闭式解。

软间隔：

允许少量样本分类错误，在目标函数中引入松弛变量   (  为合页损失(hinge loss))，

引入C>0，惩罚参数，C越大说明把错误放的越大。

 其中，

软间隔求解

与硬间隔类似：

上式的拉格朗日函数为：

 满足KKT条件，转换成对偶问题：

先求内部最小值，对 w , b  和  求偏导并令其等于 0 可得： 

 将其代入到上式中去可得到，注意  被消掉了

 此时需要求解  ，同样利用SMO（序列最小优化）算法。

核函数

将两个低维空间中的向量映射到高维空间后的内积

为什么SVM只使用支持向量？

---

随机森林

常见调参：
n_estimators:森林中决策树的个数，默认是10
criterion：度量分裂质量，信息熵或者基尼指数
max_features：特征数达到多大时进行分割
max_depth:树的最大深度
min_samples_split:分割内部节点所需的最少样本数量
bootstrap:是否采用有放回式的抽样方式
min_impurity_split：树增长停止的阀值

XGB

常用调参：

n_estimators:迭代次数，子树的数量
max_depth、min_child_weigh：树深，孩子节点最小样本权重和
gamma、alpha、lambda：后剪枝比例，L1，L2正则化系数
subsample、colsample_bytree：样本采样、列采样
eta:削减已学树的影响，为后面学习腾空间
tree_method：gpu_histGPU 加速

一篇文章搞定GBDT、Xgboost和LightGBM的面试 - 知乎GBDT和XGB基本上是机器学习面试里面的必考题。最近面试了五十场面试，基本三分之二的面试官都问了关于GBDT和XGB的问题。 下面把里面常用的知识点、常见的面试题整理出来 首先来说集成学习 集成学习boosting 串行的…https://zhuanlan.zhihu.com/p/148050748