【图论】—— Bellman-Ford算法和SPFA算法
给定一张有向图,若对于图中的某一条边 ![]() ,有
,有 ![]() 成立,则称该边满足三角形不等式。如果所有边都满足三角形不等式,则
成立,则称该边满足三角形不等式。如果所有边都满足三角形不等式,则 ![]() 数组就是所求的最短路。
数组就是所求的最短路。
Bellman-Ford算法
![]() 表示的是一条从 x 出发, 到达 y ,长度为 z 的有向边。
表示的是一条从 x 出发, 到达 y ,长度为 z 的有向边。
首先介绍基于迭代的Bellman-Ford算法,它的流程如下:
- 扫描所有边
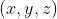 ,若
,若 ![dist[y]> dist[x]+z](http://img.e-com-net.com/image/info8/17b4744b0a9243c6ac2192d475842f49.gif) , 则用
, 则用 ![dist[x]+z](http://img.e-com-net.com/image/info8/7497e7e57ce343ce90c740937b7d784c.gif) 更新
更新 ![dist[y]](http://img.e-com-net.com/image/info8/bee5cde83ca24134810116f611236974.gif)
- 重复上述操作,直到没有更新操作发生。
Bellman-Ford算法的时间复杂度是 ![]()
通过Bellman-Ford算法我们可以求解有边数限制的最短路问题。
例题:AcWing 853. 有边数限制的最短路
算法步骤 :
- 初始化 dist 数组为正无穷, dist[1] = 0
- (外重循环)循环 i 从 1 到 n ,遍历 n 次表示:是不经过超过 i 条边到达终点的最短距离
- (内重循环)循环 i 从 1 到 m, 遍历 m 条边,把所有的边都进行松弛操作:
每次取出两点以及以及连接他们的权重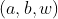
用以下公式更新最短距离:![dist[b] = min(dist[b], dist[a] + w)](http://img.e-com-net.com/image/info8/231fd97928fc4565bb1769d292356dbd.gif)
注意点:
- 需要把dist数组进行一个备份,这样防止每次更新的时候出现串联
- 由于存在负权边,所以 return -1 的条件是
![dist[n] > 0x3f3f3f3f/2](http://img.e-com-net.com/image/info8/1aaccc6c0962434f8d5d4d59a08ff5cb.gif)
代码实现 :
#include
#include
using namespace std;
const int N = 510, M = 10010;
struct Edge
{
int a, b, w;
}e[M]; // 存下每一条即可
int dist[N];
int back[N]; // 备份数组放置串联
int n, m, k;
void bellman_ford()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for(int i = 0; i < k; i ++ ) // 不超过k条边
{
memcpy(back, dist, sizeof back);
for(int j = 0; j < m; j ++ ) // 遍历所有边
{
int a = e[j].a, b = e[j].b, w = e[j].w;
dist[b] = min(dist[b], back[a] + w);
}
}
}
int main()
{
cin >> n >> m >> k;
for(int i = 0; i < m; i ++ )
{
int a, b, w;
scanf("%d%d%d", &a, &b, &w);
e[i] = {a, b, w};
}
bellman_ford();
if(dist[n] > 0x3f3f3f3f / 2) puts("impossible");
else cout << dist[n] << endl;
return 0;
} SPFA算法
SPFA算法在国际上通称为“队列优化的“Bellman-Ford算法”。
SPFA算法的流程如下:
- 建立一个队列,起初队列中只含有起点1
- 取出头结点 x ,扫描它的所有出边
,若
,则使
用
用来更新。同时若y不再队列中,则将y入队
在任意时刻,该算法的队列都保持了该拓展的节点。每次入队都相当于完成了一次 dist 数组的更新操作,使其满足三角不等式。一个节点可能会入队、出队多次。最终,图中所有的结点全部收敛到全部满足三角不等式的状态。
这个队列避免了对Bellman-Ford算法中不需要拓展的多余结点的冗余扫描,在随机图上的运行效率为 ![]() 级别,其中 k 是一个很小的常数。
级别,其中 k 是一个很小的常数。
代码实现:SPFA求最短路
#include
#include
#include
#include
using namespace std;
const int N = 1e6 + 10;
int n, m;
int h[N], e[N], w[N], ne[N], idx;
int dist[N];
bool st[N];
void add(int a, int b, int c)
{
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++ ;
}
void spfa()
{
memset(dist, 0x3f, sizeof dist);
queue q;
dist[1] = 0;
st[1] = true;
q.push(1);
while(q.size())
{
int t = q.front();
q.pop();
st[t] = false;
for(int i = h[t]; ~i; i = ne[i])
{
int j = e[i];
if(dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
if(!st[j])
{
q.push(j);
st[j] = true;
}
}
}
}
}
int main()
{
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c);
}
spfa();
if(dist[n] == 0x3f3f3f3f) puts("impossible");
else printf("%d",dist[n]);
return 0;
}

