scikit-learn机器学习笔记——KMeans聚类
scikit-learn机器学习笔记——KMeans聚类
- KMeans步骤
- KMeans API
- KMeans性能评估指标
-
- Kmeans性能评估指标API
- KMeans应用实例
KMeans步骤
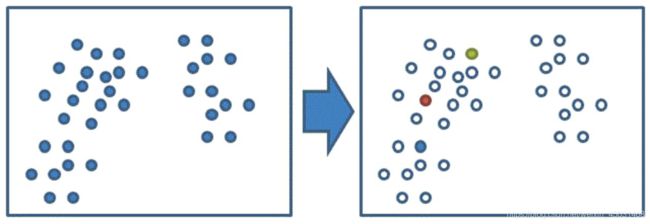
1、随机设置K个特征空间内的点作为初始的聚类中心;
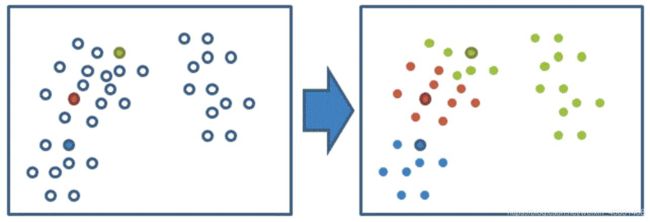
2、对于其他每个点计算到K个中心的距离,未知的点选择最近的一个聚类 中心点作为标记类别;
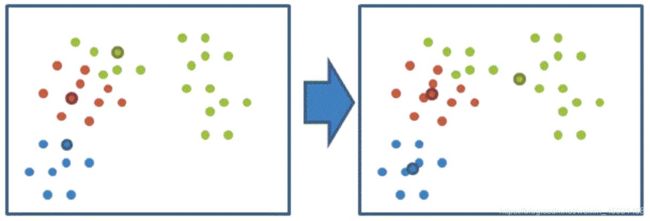
3、接着对着标记的聚类中心之后,重新计算出每个聚类的新中心点(平均值);
4、如果计算得出的新中心点与原中心点一样,那么结束,否则重新进行 第二步过程。
KMeans API
• sklearn.cluster.KMeans(n_clusters=,init=‘k-means++’)
• k-means聚类
• n_clusters:开始的聚类中心数量
• init:初始化方法,默认为’k-means ++’
• labels_:默认标记的类型,可以和真实值比较(不是值比较)
KMeans性能评估指标
轮廓系数:
s c i = b i − a i max ( b i , a i ) \begin{aligned} &\text { } s c_{i}=\frac{b_{i-} a_{i}}{\max \left(b_{i}, a_{i}\right)} \end{aligned} sci=max(bi,ai)bi−ai
注 : 对于每个点 i i i 为已聚类数据中的样本, b i b_{i} bi 为 i i i 到其它族群的所有样本的平均 距离, a i a_{i} ai 为 i i i 到本身族的距离平均值。
最终计算出所有的样本点的轮廓系数平均值。
如果 s c i s c_{i} sci 小于0,说明 a i a_{i} ai 的平均距离大于最近的其他族。 聚类效果不好。
如果 s c i s c_{i} sci 越大,说明 a i a_{i} ai 的平均距离小于最近的其他族。 聚类效果好。
轮廓系数的值是介于 [-1,1],越趋近于1代表内聚度和分离度都相对较优。
Kmeans性能评估指标API
• sklearn.metrics.silhouette_score(X, labels)
• 计算所有样本的平均轮廓系数
• X:特征值
• labels:被聚类标记的目标值
KMeans应用实例
from sklearn.cluster import KMeans
import pandas as pd
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
from sklearn.metrics import silhouette_score
aisles = pd.read_csv('./aisles.csv')
prior = pd.read_csv('./order_products__prior.csv')
orders = pd.read_csv('./orders.csv')
products = pd.read_csv('./products.csv')
mg1 = pd.merge(aisles, products, left_on='aisle_id',right_on='aisle_id')
mg2 = pd.merge(mg1, prior, left_on='product_id', right_on='product_id')
mg3 = pd.merge(mg2, orders, left_on='order_id', right_on='order_id')
cross = pd.crosstab(mg3['user_id'], mg3['aisle'])
print(cross.head(5))
print(cross.shape)
pca = PCA(n_components=0.9)
pca_cross = pca.fit_transform(cross)
print(pca_cross.shape)
X_train = pca_cross[:300]
km = KMeans(n_clusters=3)
km.fit(X_train)
pre = km.predict(X_train)
colors = ['orange', 'red', 'blue']
colr = [colors[i] for i in pre]
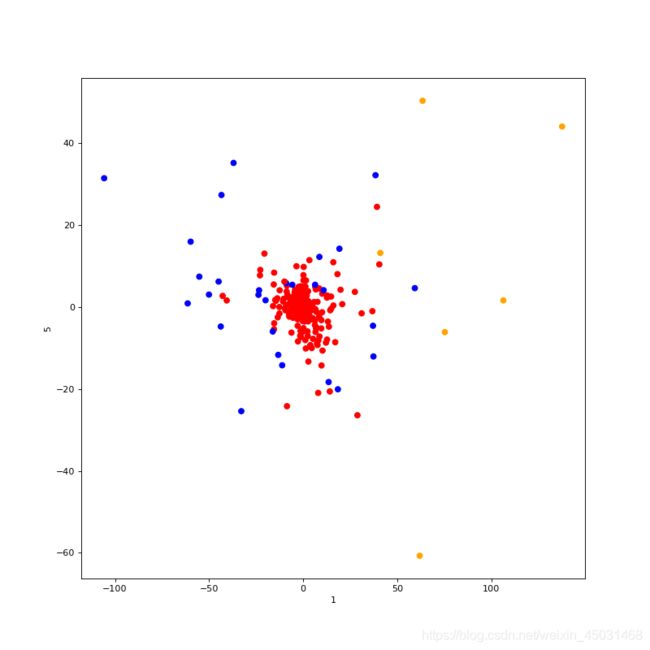
plt.figure(figsize=(10,10), dpi=80)
plt.scatter(X_train[:,1], X_train[:,5], color=colr)
plt.xlabel('1')
plt.ylabel('5')
plt.show()
score = silhouette_score(X_train, pre)
print("平均轮廓系数:", score)
aisle air fresheners candles asian foods ... white wines yogurt
user_id ...
1 0 0 ... 0 1
2 0 3 ... 0 42
3 0 0 ... 0 0
4 0 0 ... 0 0
5 0 2 ... 0 3
[5 rows x 134 columns]
(206209, 134)
(206209, 27)
平均轮廓系数: 0.656079899994259