集体智慧学习编程—— 学习笔记一
学习目标:
1、利用博客资源自我创建数据集;
2、利用皮尔逊相关度描述单个数据之间的紧密度;
3、对从新浪博客爬取的博客进行分类;
4、绘制树状图。
一、利用博客资源创建数据集:
我这里选取的是新浪博客,例如http://roll.finance.sina.com.cn/blog/blogarticle/cj-bkks/inde_1.shtml, 其中url中数字1是页码。基于这个规律,可以抓取很多很多博客来充实数据集。
为了实现博客的抓取,这里我写了一个小爬虫,因为这不是学习的重点,这里就直接上代码了,我都写了注释的:
注意,我的运行环境是python2.7.
# -*- coding: utf-8 -*-
import urllib
from bs4 import BeautifulSoup
import codecs
import jieba
from collections import Counter
#获取当页所有博客的url,以list的方式返回
def get_all_urls(url):
content = urllib.urlopen(url).read()
soup = BeautifulSoup(content, 'lxml') #利用beautifsoup进行html的解析
url_list = list()
for item in soup.find_all('ul', class_ = 'list_009'):
for i in item.find_all('li'): url_list.append(i.a['href'])
return url_list
#输入博客的url,返回博客内容
def get_content(url):
text = urllib.urlopen(url).read()
soup = BeautifulSoup(text, 'lxml')
content = soup.find('div', class_ = 'articalContent').get_text()
return content
words_list = list() #标记词列表
dd = dict()
for i in range(1, 20):
page = 'http://roll.finance.sina.com.cn/blog/blogarticle/cj-bkks/inde_' + str(i) + '.shtml'
url_list = get_all_urls(page)
for i in range(len(url_list)):
url = url_list[i]
content = get_content(url).strip()
filename = str(i) + '.txt'
file = codecs.open(filename, 'w', encoding = 'utf-8') #打开文档文件,存入每一篇博客内容
file.write(content)
file.close
for words in jieba.cut(content, cut_all = False): #利用结巴分词,对中文分词,获取标记词列表
words_list.append(words)
print i
i = i + 1
d = Counter(words_list) #对标记词列表中进行统计处理,Counter返回一个字典,key是标记词,value是出现的次数
l = list() #对字典进行‘排序’
for k,v in d.items():
l.append((v,k))
l.sort(reverse = True)
file = codecs.open('frequency.txt', 'w', encoding = 'utf-8')
for item in l:
if item[0] > 4 and item[0] < 80: #去除出现频率过高或者过低的词,可以自己改动了。最后存入frequency.txt文档
file.write(item[1] + '\r\n')
此时在你python程序运行的文件夹中就会出现很多txt文本文件:
二、利用皮尔逊相关度描述单个数据之间的紧密度:
一般用欧几里德距离和皮尔逊相关度来评价数据之间的相似程度,或者是紧密度。相比较而言,欧几里德距离更加直观,因此一般而言也采用的更多一点,如果是比较简单的情况下。但是这里我采用的是后者,因为可能会有些博客字数较少(很多),使得这些博客包含更少(更多)的词汇,这样使得欧几里德距离会很大。皮尔逊相关法从直观的意义上来讲,是两数据拟合直线的比较,数据点更多只是意味着拟合直线更加精确,因此可以很好的纠正这种误差。这里代表每篇博客的特征是一个对标记词统计后的list。
这里贴出皮尔逊相关法的代码:(http://lobert.iteye.com/blog/2024999,大家也可以看看这篇文章)
def distance(item1, item2):
sum1 = sum(item1)
sum2 = sum(item2)
sum1sq = sum([pow(v, 2) for v in item1])
sum2sq = sum([pow(v, 2) for v in item2])
psum = sum([item1[i] * item2[i] for i in range(len(item1))])
num = psum - (sum1 *sum2 / len(item1))
den = sqrt(sum1sq - pow(sum1, 2)/len(item1)) * (sum2sq - pow(sum2, 2)/ len(item1))
if den == 0 : return 0
else: return 1 - num/den
三、对从新浪博客爬取的博客进行分类:
我们现在已经获得了标记词、每篇博客的内容以及评价博客之间相关关系的方法,接下来我们就来对博客进行分级聚类。
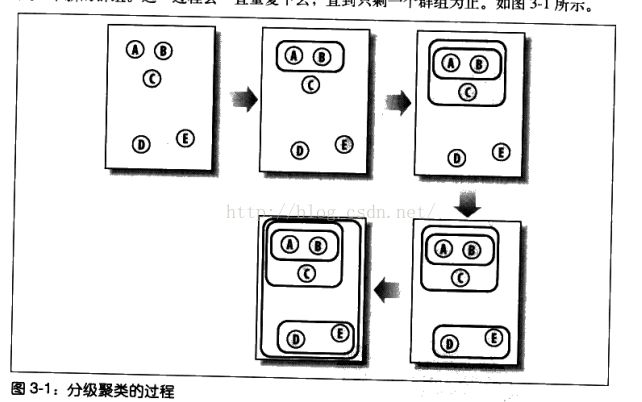
分级聚类是通过不断将最相似的群组两两合并,来构造出一个群组的层级结构,如下图:
因为我们是对博客进行分类,这里把上图中的A,B,C,D,E看成是5篇博客。首先利用皮尔逊相关度来两两评价博客之间的紧密度,然后找出紧密度最小的两篇博客,这里是AB。将AB博客的特性list合并(相加求平均值),组成一个新“博客”,然后对AB,C,D,E一共4篇博客两两计算紧密度,找出紧密度最小的一组博客。重复上述过程,直至将所有博客聚类成一组。对上述最终结果进行可视化处理,即可用树状图来表示:
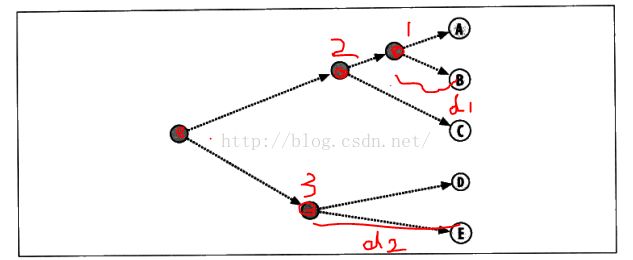
树状图可以非常直观地来显示我们分级聚类的结果。节点间的距离代表了之间的紧密度。如:d1是节点1与A、B的距离;d2是节点3与D、E之间的距离。虽然节点1和节点2都仅有一个分支,但是d2大于d1,意味着AB之间的紧密度比DE之间的紧密度更加亲密,也就是皮尔逊相关度更高。
接下来我们对每篇博客进行描述,因此建立了一个类:
class cluster:
def __init__(self, w_list = None, left = None, right = None, node_id = 0, distance = 0.0):
self.w_list = w_list #特征list
self.node_id = node_id #节点id
self.left = left #左节点
self.right = right #右节点
self.distance = distance #离左右节点的距离
例如对上图中节点1的描述:w_list是A、B博客特征list的平均值,left是A博客,right是B博客,distance是d1的长度。若来描述A,则left和rigth都是None。然后读取我们抓取的每一篇博客,并创建cluster类,组成cluster_list。
words_list = []
cluster_list = list()
file = codecs.open('frequency.txt', 'r') #打开标记特性词的文档
for line in file:
line.strip()
words_list.append(line) #标记特征词的list
for i in range(100): #打开每一篇博客
filename = str(i) + '.txt'
try:
file = codecs.open(filename, 'r')
content = file.read()
l = []
for word in words_list:
l.append(content.count(word)) #每一个标记词在这篇博客中出现的次数
cluster_list.append(cluster(w_list = l, node_id = i)) #为这篇博客创建类并append到cluster_list中
except: break
然后我们进行分级聚类:
def clustering(cluster_list):
k = -1
while(len(cluster_list) > 1):
dmin = distance(cluster_list[0].w_list, cluster_list[1].w_list)
for i in range(len(cluster_list)): #两两比较,找出最小的
for j in range(i + 1, len(cluster_list)):
dis = distance(cluster_list[i].w_list, cluster_list[j].w_list)
if dis < dmin or dis == dmin:
dmin = dis
cluster1 = cluster_list[i]
cluster2 = cluster_list[j]
l = [(cluster1.w_list[i] + cluster2.w_list[i])/2.0 for i in range(len(cluster1.w_list))]
newcluster = cluster(w_list = l, left = cluster1, right = cluster2, node_id = k, distance = dmin) #将紧密度最高的两个cluster进行合并重组
cluster_list.append(newcluster) #将合并后的cluster添加如cluster_list
cluster_list.remove(cluster1)
cluster_list.remove(cluster2) #移除紧密度最高的两个cluster
k = k - 1 #若node_id为负数,则表示这不是叶节点
return cluster_list[0]
补充:当然了,也可以利用PIL来画树状图。如果大家是win7 64位的系统,推荐大家去http://www.lfd.uci.edu/~gohlke/pythonlibs/进行下载,下载pillow这个包。这个网站上的库都是已经编译好了的,下载后直接安装即可。绘图也不是很麻烦,在绘图时,我突然意识到cluster类中定义left和right的巧妙之处。如果大家有时间也可以画画这个树状图,由于不是学习的主要内容这里就不详细再说了~效果应该大致是这样的:
祝大家学习愉快!
我是一只小蜗牛,看我来慢慢爬上python这座山峰!