煤炭价格预测：基于matlab的时间序列分析（主要流程+完整代码）

案例简介

结合秦皇岛港动力煤价格的历史数据(附件1)，以及问题1中的影响煤炭价格的主要因素，建立煤炭价格预测模型，分别以天、周、月为单位，预测未来31天、35周、36个月的煤炭价格。

时间序列简介

平稳时间序列{xt}

确定性序列:若序列x(n)在任意时刻n时的值能够被精确地确定(或是被预测)，那么，我们说x(n)是一个确定性的序列，如我们熟知的正弦序列、周期脉冲序列等。

平稳时间序列：时间序列行为不随时间改变
一组数列如下表示

数列示意图

ARIMA=AR+MA+INTEGRATER

自回归AR：利用自身历史值预测

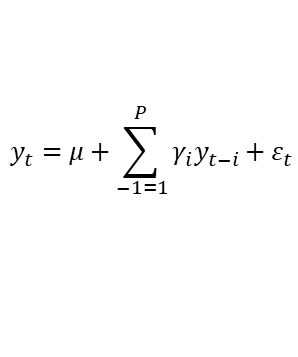
移动平均MA：关注自回归模型中的误差项

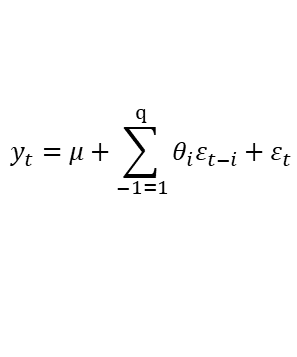
_当前值， 常数项，_误差（白噪音），阶数, ——人为定义，相关系数_,_——求解

整合INTEGRATER：差分法平稳化处理：计算时间序列中t时刻与t-1时刻的差值，从而得到一个新的、更平稳的时间序列。

实例应用

数据平稳化

单位根检验
ADF
KPSS

###代码

y_h_adf = adftest(Y)
y_h_kpss = kpsstest(Y)

输出 y_h_adf = 1；y_h_kpss =0通过检验

*一阶差分：d=1

模型选择——确定p、q

ACF/PACF图法（不推荐）

代码


PACF最后一个在蓝线外（即阈值外）的Lag值就是p值；ACF最后一个在蓝线外（即阈值外）的Lag值就是q值。

根据最佳lags值确定

为了确定最好的滞后，用不同的滞后选择拟合几个模型。这里，适合所有p = 1…，4, q = 1，…、4的组合(共16款)。存储每个拟合模型的对数似然目标函数和系数数目。
下面展示示例

LOGL = zeros(4,4); % Initialize
PQ = zeros(4,4);
for p = 1:4
    for q = 1:4
        Mdl = arima(p,0,q);
        [EstMdl,~,logL] = estimate(Mdl,Y,'Display','off');
        LOGL(p,q) = logL;
        PQ(p,q) = p + q;
     end
end

计算每个拟合模型的BIC。模型中的参数数为p + q + 1(对于AR和MA系数，以及常数项)。在数据集中观测的次数是100。

LOGL = reshape(LOGL,16,1);
PQ = reshape(PQ,16,1);
[~,bic] = aicbic(LOGL,PQ+1,100);
reshape(bic,4,4)

ans = 4×4

108.6241 105.9489 109.4164 113.8443
99.1639 101.5886 105.5203 109.4348
102.9094 106.0305 107.6489 99.6794
107.4045 100.7072 102.5746 102.0209

---

在输出的BIC矩阵中，行对应AR度( p )，列对应MA度( q )，值越小越好。

代码

函数

Arima：创建单变量自回归综合移动平均(ARIMA)模型
Estimate：拟合自回归积分滑动平均(ARIMA)模型
log L：优化的对数似然目标函数值，作为数值标量返回。
Aicbic：计算信息标准，评估模型的适足性
aic：最小化信息量准则
=−2()+2
L 表示模型的极大似然函数， K 表示模型参数个数。
bic：贝叶斯信息准则，最小越好
=−2()+()
N表示样本容量

模型检验

代码

预测

函数

Forecast：预测ARIMA或ARIMAX模型响应或条件方差

【预测值（最小均方差），均方差】=forecast（arima模型，步长，初始数据）

代码

结果

单步预测

代码

结果

完整代码

只需要更改数据，就可以完成你的预测！
来，试试看

Y=[417 421 421 435 450 457 470 469 467 459 447 442 445 448 453 458 462 467 479 490 497 505 520 578 618 603 595 595 615 690 830 925 865 870 870 875 808 580 595 598 570 558 558 578 585 580 568 565 570 575 600 630 650 720 780 805 765 685 680 705 760 755 755 745 730 745 798 803 780 775 765 765 793 818 838 848 853 835 830 830 845 855 845 830 793 780 765 770 783 780 763 680 643 628 630 630 640 640 635 630 625 625 625 620 615 610 608 603 588 565 548 535 533 540 555 575 598 600 600 573 540 530 530 535 535 530 515 495 475 475 475 495 503 505 510 510 500 485 455 433 405 415 410 410 400 395 385 370 365 365 370 375 375 385 385 385 385 395 400 420 465 490 560 610 700 672 650 621 610 605 635 655 620 565 585 625 645 630 645 725 710 675 690 710 750 730 655 595 595 655 700 680 655 625 625 635 675 647.5 632.5 595 585 592.5 602.5 627.5 625 620 615 595 610 595 580 582.5 587.5 577.5 552.5 552.5 552.5 562.5 572.5 572.5 552.5 510 475 ]
%Y为2006/7/3 - 2020/4/30的秦皇岛动力煤历史价格
plot(Y)

figure
autocorr(Y)
figure
parcorr(Y)
%ACF和PACF图

y_h_adf = adftest(Y)
y_h_kpss = kpsstest(Y)
%平滑性检验,yd1_h_adf =1，yd1_h_kpss =0，通过检验

Yd1 = diff(Y);
% 一阶差分，结果平稳。如果依旧不平稳的话，再次求差分，直至通过检验
yd1_h_adf = adftest(Yd1)
yd1_h_kpss = kpsstest(Yd1)
Yd1=Yd1'
Y=Y'
%Yd2转换成列向量



LOGL = zeros(4,4); % Initialize
PQ = zeros(4,4);
for p = 1:4
    for q = 1:4
        Mdl = arima(p,1,q);
        [~,~,logL] = estimate(Mdl,Yd1,'Display','off');
        LOGL(p,q) = logL;
        PQ(p,q) = p + q;
     end
end

LOGL = reshape(LOGL,16,1);
PQ = reshape(PQ,16,1);
[~,bic] = aicbic(LOGL,PQ+1,100);

a=reshape(bic,4,4)
%reshape 重构数组

a_max=max(a(:));
[x,y]=find(a==min(a(:)));

%找最佳lags值 x=2，y=1，即对应ARMA（2，1）模型

Mdl = arima(x, 1, y);  %第二个变量值为1，即一阶差分
EstMdl = estimate(Mdl,Y);
[res,~,logL] = infer(EstMdl,Y);   %res即残差

stdr = res/sqrt(EstMdl.Variance);
figure('Name','残差检验')
subplot(2,3,1)
plot(stdr)
title('Standardized Residuals')
subplot(2,3,2)
histogram(stdr,10)
title('Standardized Residuals')
subplot(2,3,3)
autocorr(stdr)
subplot(2,3,4)
parcorr(stdr)
subplot(2,3,5)
qqplot(stdr)
%上图为残差检验的结果图。
% Standardized Residuals是查看残差是否接近正态分布，理想的残差要接近正态分布；
% ACF和PACF检验残差的自相关和偏自相关，理想的结果应该在图中不存在超出蓝线的点；
% 最后一张QQ图是检验残差是否接近正太分布的，理想的结果中蓝点应该靠近红线。

% Durbin-Watson 统计是计量经济学分析中最常用的自相关度量
diffRes0 = diff(res);  
SSE0 = res'*res;
DW0 = (diffRes0'*diffRes0)/SSE0 % Durbin-Watson statistic，
% 该值接近2，则可以认为序列不存在一阶相关性。

%% 5.预测
step = 20; %预测步数为20
[forData,YMSE] = forecast(EstMdl,step,'Y0',Y);   
lower = forData - 1.96*sqrt(YMSE); %95置信区间下限
upper = forData + 1.96*sqrt(YMSE); %95置信区间上限

figure()
plot(Y,'Color',[.7,.7,.7]);
hold on
h1 = plot(length(Y):length(Y)+step,[Y(end);lower],'r:','LineWidth',2);
plot(length(Y):length(Y)+step,[Y(end);upper],'r:','LineWidth',2)
h2 = plot(length(Y):length(Y)+step,[Y(end);forData],'k','LineWidth',2);
legend([h1 h2],'95% 置信区间','预测值',...
	     'Location','NorthWest')
title('Forecast')
hold off

⭐以上只涉及时间序列预测很基础的部分。更深的理论分析可以参考关于时间序列分析的书籍。matlab中有很多帮助分析简化步骤的函数，对于初学者而言是个特别棒的工具

参考资料

知乎：https://zhuanlan.zhihu.com/p/69630638
书籍：matlab在时间序列分析中的应用