深入理解梅尔刻度、梅尔滤波器组和梅尔时频谱图
前情提要
短时傅里叶变换公式
S ( m , k ) = ∑ n = 1 N − 1 x ( n + m H ) w ( n ) e − i 2 π k N n S(m,k) = \sum_{n=1}^{N-1} x(n+mH)w(n)e^{-i2 \pi \frac{k}{N} n} S(m,k)=n=1∑N−1x(n+mH)w(n)e−i2πNkn
其中,m是当前滤波器的序号,表征了当前的时间段,k是当前频率的序号,表征了当前正在对哪一频率的 e − i 2 π k N n e^{-i2 \pi \frac{k}{N} n} e−i2πNkn 信号,寻找最佳的振幅和初相,w(n)是窗函数。更多关于短时傅里叶变换的知识,请参考深入理解傅里叶变换(四)。
本文要讲解的梅尔时频谱图,需要有时频谱图的知识,也可参考深入理解傅里叶变换(四)。
梅尔刻度
人耳对音高(pitch)的感知是非线性的,当声音频率线性增加时,我们不会感觉音高也是线性增加的。为了将人耳对音高的线性感知刻画出来,我们需要梅尔刻度,梅尔刻度本质上是关于频率的函数,将赫兹(Hz)映射为梅尔(mel):
m = 2595 l o g 10 ( 1 + f 700 ) = 1127 l n ( 1 + f 700 ) m = 2595 log_{10}(1+\frac{f}{700}) = 1127 ln(1+\frac{f}{700}) m=2595log10(1+700f)=1127ln(1+700f)
从公式可见,对数部分可以以自然对数为底数,也可以以10为底数,不同的底数对应不同的系数,要确定当前的系数,只需要代入(1000Hz, 1000mel)即可。
我们不仅好奇,既然人耳对音高的感知是非线性的,为什么梅尔刻度会过(1000Hz, 1000mel)这个点呢?原因是人耳对低频部分的感知是近似线性的,这个低频部分大概是0Hz~1000Hz,因此梅尔刻度也过(0Hz, 0mel)点,梅尔刻度图上也可看出该低频部分是近似线性的:

从梅尔刻度到赫兹的映射如下:
f = 700 ( 1 0 m 2595 − 1 ) = 700 ( e m 1127 − 1 ) f = 700(10^{\frac{m}{2595}}-1) = 700(e^{\frac{m}{1127}}-1) f=700(102595m−1)=700(e1127m−1)

现在,当梅尔刻度线性增加,赫兹呈现对数增加,人耳对这样变化的音高的感知是线性的。
梅尔时频谱图
梅尔时频谱图(Mel spectrogram)是同时考虑了三个要素,而绘制出来的:
- 对一段音频的时、频、谱信息同时呈现
时频谱图就是干这个的。 - 对响度(loudness)的度量,要与人耳对响度的感知线性相关
可以将振幅的平方转成分贝来实现。 - 对音高的度量,要与人耳对音高的感知线性相关
这就需要利用梅尔刻度得到梅尔滤波器组,对原始的时频谱图进行滤波来实现了。
梅尔滤波器组
使用梅尔滤波器组的步骤有三:
- 选定滤波器组的个数 n m e l s n_{mels} nmels
个数取决于我们要研究的问题,常用40、60、90、128,现在就取一个小一点的数:6,方便读图。 - 建立滤波器组
分为4个步骤:- 确定要进行滤波的频率范围,即选取最小频率 f l f_{l} fl 和最大频率 f h f_{h} fh ,通常最小频率选为0,最大频率选为奈奎斯特频率 s r 2 \frac{s_r}{2} 2sr,然后把这两个频率值转为梅尔刻度 m l m_{l} ml 和 m h m_{h} mh 。
- 将 m l m_{l} ml 和 m h m_{h} mh 连成一条线,然后在这条线上,均等地取 n m e l s n_{mels} nmels 个点,得到序列 { m 1 , m 2 , . . . , m n m e l s } \left \{ m_1,m_2,...,m_{n_{mels}} \right \} {m1,m2,...,mnmels}。由于此时采用了梅尔刻度,所以人耳对这些点对应的音高是线性感知的。
- 把这些点都转成赫兹,得到序列 { f 1 , f 2 , . . . , f n m e l s } \left \{ f_1,f_2,...,f_{n_{mels}} \right \} {f1,f2,...,fnmels}。注意在转成赫兹时,需要对这些点进行舍入,使这些点在 { 0 , 1 n f f t s r , 2 n f f t s r , . . . , n f f t / 2 n f f t s r } \left \{0,\frac{1}{n_{fft}} s_r,\frac{2}{n_{fft}} s_r,...,\frac{n_{fft}/2}{n_{fft}} s_r \right \} {0,nfft1sr,nfft2sr,...,nfftnfft/2sr} 一共 ( 1 + n f f t 2 ) (1+\frac{n_{fft}}{2}) (1+2nfft) 个频率上,能一一对应。用数学语言表述:
∀ f i , f i ∈ { 0 , 1 n f f t s r , 2 n f f t s r , . . . , n f f t / 2 n f f t s r } , i = 1 , 2 , . . . , n m e l s \forall f_i, f_i \in \left \{0,\frac{1}{n_{fft}} s_r,\frac{2}{n_{fft}} s_r,...,\frac{n_{fft}/2}{n_{fft}} s_r \right \} ,i=1,2,...,n_{mels} ∀fi,fi∈{0,nfft1sr,nfft2sr,...,nfftnfft/2sr},i=1,2,...,nmels - 根据序列 { f 1 , f 2 , . . . , f n m e l s } \left \{ f_1,f_2,...,f_{n_{mels}} \right \} {f1,f2,...,fnmels} 绘制下图:
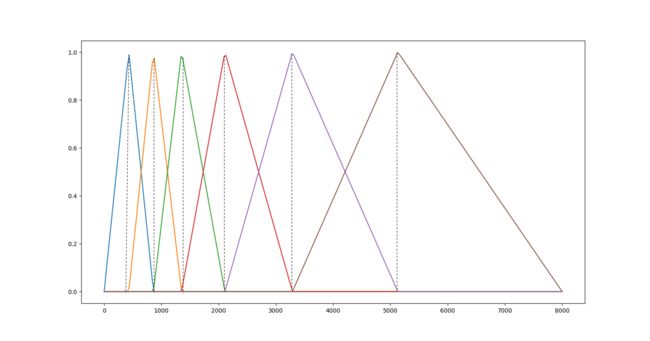
图中共有 n m e l s n_{mels} nmels 个顶点,这些顶点的横坐标为 { f 1 , f 2 , . . . , f n m e l s } \left \{ f_1,f_2,...,f_{n_{mels}} \right \} {f1,f2,...,fnmels},纵坐标都为1,第一个三角形的左顶点为 f l f_{l} fl,上顶点为 f 1 f_{1} f1,右顶点为 f 2 f_{2} f2;第二个三角形的左顶点为 f 1 f_{1} f1,上顶点为 f 2 f_{2} f2,右顶点为 f 3 f_{3} f3,以此类推,直至最后个三角形的左顶点为 f m e l s − 1 f_{mels-1} fmels−1,上顶点为 f m e l s f_{mels} fmels,右顶点为 f h f_{h} fh。
三角形的纵坐标的意义是:对应横坐标频率的权重值。梅尔滤波器组可表示为一个二维矩阵,shape为 [ n m e l s , 1 + n f f t 2 ] [n_{mels},1+\frac{n_{fft}}{2}] [nmels,1+2nfft]。
注意,一个梅尔滤波器,对于三角形外的频率也是有权重的,只不过都为0。
- 对时频谱图滤波
时频谱图也可以表示为一个二维矩阵,shape为 [ 1 + n f f t 2 , f r a m e s ] [1+\frac{n_{fft}}{2},frames] [1+2nfft,frames],如果还记得线性代数的话,记梅尔滤波器组为M,时频谱图为Y,那么滤波的计算结果就是M和Y的矩阵乘积,即第一个矩阵的列数和第二个矩阵的行数相同时,才能进行的运算,运算结果的shape为【第一个矩阵的行数,第二个矩阵的列数】,即 [ n m e l s , f r a m e s ] [n_{mels},frames] [nmels,frames]。
演示
读取一段音频,使用短时傅里叶变换,得到普通的时频谱图,然后绘制梅尔滤波器组,值得注意的是,librosa的梅尔滤波器组函数还带有权重归一化功能,即对一个三角形滤波器的每个权重,都除以该三角形的面积,如果不希望进行该归一化,设置参数 norm=None,即 melfb = librosa.filters.mel(sr=sr, n_fft=N_FFT, n_mels=N_MELS, norm=None)。
import librosa
import librosa.display
import matplotlib.pyplot as plt
import numpy as np
if "__main__" == __name__:
debussy_path = r"16 - Extracting Spectrograms from Audio with Python\audio\debussy.wav"
signal, sr = librosa.load(path=debussy_path, sr=16000)
N_FFT = 512
N_MELS = 6
stft = librosa.stft(y=signal,
n_fft=N_FFT,
hop_length=sr // 100,
win_length=sr // 40)
freq = librosa.fft_frequencies(sr=sr, n_fft=N_FFT)
power, phase = librosa.magphase(stft, power=2)
melfb = librosa.filters.mel(sr=sr, n_fft=N_FFT, n_mels=N_MELS)
plt.plot(freq, np.transpose(melfb))
plt.show()

直接矩阵乘积,然后将振幅的平方转为分贝,绘制梅尔时频谱图,注意一定要先滤波,再转分贝。
import librosa
import matplotlib.pyplot as plt
import librosa.display
import numpy as np
if "__main__" == __name__:
# m = np.linspace(0, 2600, 2600 + 1)
# f = 700 * (np.exp(m / 1127) - 1)
# plt.plot(m, f)
# plt.xlabel("Mel Frequency(mel)")
# plt.ylabel("Frequency(Hz)")
debussy_path = r"16 - Extracting Spectrograms from Audio with Python\audio\debussy.wav"
signal, sr = librosa.load(path=debussy_path, sr=16000)
N_FFT = 512
N_MELS = 6
stft = librosa.stft(y=signal,
n_fft=N_FFT,
hop_length=sr // 100,
win_length=sr // 40)
freq = librosa.fft_frequencies(sr=sr, n_fft=N_FFT)
power, phase = librosa.magphase(stft, power=2)
melfb = librosa.filters.mel(sr=sr, n_fft=N_FFT, n_mels=N_MELS)
# plt.plot(freq, np.transpose(melfb))
melspec = np.matmul(melfb, power)
melspec_db = librosa.power_to_db(melspec)
# plt.subplot(2, 1, 1)
librosa.display.specshow(melspec_db,
sr=sr,
n_fft=N_FFT,
hop_length=sr // 100,
win_length=sr // 40,
x_axis="s",
y_axis="mel")
plt.colorbar(format="%+2.f db")
plt.show()
import librosa
import matplotlib.pyplot as plt
import librosa.display
import numpy as np
if "__main__" == __name__:
# m = np.linspace(0, 2600, 2600 + 1)
# f = 700 * (np.exp(m / 1127) - 1)
# plt.plot(m, f)
# plt.xlabel("Mel Frequency(mel)")
# plt.ylabel("Frequency(Hz)")
debussy_path = r"16 - Extracting Spectrograms from Audio with Python\audio\debussy.wav"
signal, sr = librosa.load(path=debussy_path, sr=16000)
N_FFT = 512
N_MELS = 6
stft = librosa.stft(y=signal,
n_fft=N_FFT,
hop_length=sr // 100,
win_length=sr // 40)
freq = librosa.fft_frequencies(sr=sr, n_fft=N_FFT)
power, phase = librosa.magphase(stft, power=2)
melfb = librosa.filters.mel(sr=sr, n_fft=N_FFT, n_mels=N_MELS)
# plt.plot(freq, np.transpose(melfb))
melspec = np.matmul(melfb, power)
melspec_db = librosa.power_to_db(melspec)
plt.subplot(2, 1, 1)
librosa.display.specshow(melspec_db,
sr=sr,
n_fft=N_FFT,
hop_length=sr // 100,
win_length=sr // 40,
x_axis="s",
y_axis="mel")
plt.colorbar(format="%+2.f db")
S = librosa.feature.melspectrogram(y=signal,
sr=sr,
n_fft=N_FFT,
hop_length=sr // 100,
win_length=sr // 40,
n_mels=N_MELS)
S_dB = librosa.power_to_db(S)
plt.subplot(2, 1, 2)
librosa.display.specshow(S_dB,
sr=sr,
n_fft=N_FFT,
hop_length=sr // 100,
win_length=sr // 40,
x_axis="s",
y_axis="mel")
plt.colorbar(format="%+2.f db")
np.testing.assert_array_almost_equal(S_dB, melspec_db)
plt.show()
下一节讲MFCC,梅尔频率倒谱系数(Mel Frequency Cepstrum Coefficient, MFCC)。

