利用python进行pid仿真控制
一、控制对象:二阶震荡环节
1. 控制系统框图如下
1.2 初始条件
y ( 0 ) = 0 u ( 0 ) = 0 e ( 0 ) = 0 r = 1 y(0)=0\quad u(0)=0\quad e(0)=0\quad r=1 y(0)=0u(0)=0e(0)=0r=1
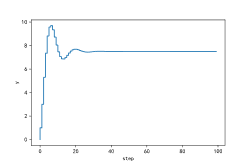
1.3 测试结果
受控系统阶跃响应曲线
二、python实现
1. 传递函数
from numpy import *
from matplotlib.pyplot import *
class Transfer: # 传递函数类
def __init__(self,num, den): # 初始化传递函数分子和分母
self.num = array(num, dtype=float); self.den = array(den[1:], dtype=float)
# 初始化历史输入和历史输出
self.x = array([0]*len(num), dtype=float); self.y = array([0]*(len(den)-1), dtype=float)
self.overflow = False # 判断是否发散震荡
def __call__(self, x):
if not self.overflow:
self.x = roll(self.x, 1); self.x[0] = x # 历史输入串入新数据
y = self.num @ self.x - self.den @ self.y # 计算输出
self.y = roll(self.y, 1); self.y[0] = y # 历史输出串入新数据
if y > 1e3: self.overflow = True
return y
else: return nan
2.PID
class PID:
def __init__(self,Kpid, pid_method=None): # 初始化PID类
# 初始化PID,历史误差
self.Kpid = array(Kpid, dtype=float); self.err = array([0]*3, dtype=float)
self.y = 0; self.overflow = False
self.q = array([Kpid[0]*(1 + Kpid[1] + Kpid[2]), -Kpid[0]*(1 + 2*Kpid[2]), Kpid[0]*Kpid[2]], dtype=float) # 计算误差系数q
self.pid_method = pid_method if pid_method != None else lambda q,err: q @ err # 选择PID方法
def __call__(self, err):
if not self.overflow:
self.err = roll(self.err, 1); self.err[0] = err # 历史误差串入新数据
self.y += self.pid_method(self.q, self.err) # 计算输出
if self.y > 1e3:
self.overflow = True
return self.y
else: return nan
3.响应参数计算
def draw(y, save=None, titleName=None): # 绘制输出阶梯图
step(range(len(y)), y)
if save != None: savefig(save)
def is_stable(y): # 判断系统是否稳定
if max(abs(y)) > 1e2: return False
dy = diff(y)
return sum(dy[int(len(dy)*0.8):]<1e-3) / (len(dy) - int(len(dy)*0.8)) > 0.8
def over_shoot(y): # 计算输出超调量
return abs(max(y) -1)
def idx_adjust(y): # 计算输出调整时间
dy = diff(y); dy_stable = (dy < 1e-3) & (dy > -1e-3)
idx = len(dy_stable) - 1
while dy_stable[idx]:
idx -= 1
if idx < 0: break
while abs(1 - y[idx]) < 2e-2:
idx -= 1
return idx + 1
4.测试类
class Analysor: # 系统pid参数测试类
def __init__(self, num, den, r, t_len): # 初始化系统的分子和分母,给定值和仿真时间
self.num = num; self.den = den; self.r = r
self.t_len = t_len; self.record = []; self.y = None
def view(self, kpid): # 仿真给定pid时系统输出
G = Transfer(self.num, self.den); pid = PID(kpid)
self.kpid=kpid; self.q = [kpid[0]*(1 + kpid[1] + kpid[2]), -kpid[0]*(1 + 2*kpid[2]), kpid[0]*kpid[2]]
y = zeros(self.t_len); u = 0; u_out = zeros(self.t_len)
for i in range(self.t_len):
y[i] = G(u)
e = self.r - y[i]
u = pid(e); u_out[i] = u
self.y = y
return y, u_out
def sort(self): # 对系统的pid记录排序
content = ''
for each in sorted(self.record):
content += repr(each)
with open('sort.txt', 'w') as f: f.write(content)
def analyse(self, kpid, auto=True): # 对给定pid值下系统响应曲线分析超调和调整时间
y = self.view(kpid) if auto else self.y
os,ts = (over_shoot(y), idx_adjust(y)) if is_stable(y) else (nan, nan)
return (os, ts)
def pid(self):
print(f'pid:{self.kpid}, q:{self.q}')
5.主程序
num, den = [0, 1, 0.5],[1, -1.5, 0.7]; pid = [0.01825, 1.3 , 3.65 ] # 系统一分子分母系数以及测试最佳pid值
r=1; y = []; t_len = 100
A = Analysor(num,den,r,t_len) # 初始化系统
y, u=A.view(pid) # 仿真最佳pid系统输出曲线,以及控制器输出曲线
draw(y)
draw(u)
print(over_shoot(y),idx_adjust(y))
链接: https://pan.baidu.com/s/1jOcjZcjDxzN8jd1NagXFrQ 提取码: k7as