PID 控制算法原理与 Python 实现
读在线广告智能出价相关的论文时,论文中基于 PID 算法设计了多变量的控制算法,既然遇到了 PID 算法相关的内容,便想着借此契机,简单总结一下 PID 算法,该算法在网上已有较多科普文章,但依旧打算整理一下,加深自己的理解。
PID 算法因为其实现简单且效果拔群的特性,而被广泛使用,比如温度控制元件、无人机飞行姿势、机器人控制等。
在控制系统理论体系中,会根据系统是否有反馈将系统分为开环系统与闭环系统,而 PID 算法是闭环系统中常用的算法,为了方便理解,这里举个具体的例子来解释开环系统与闭环系统:
我开发了一个机器人,在一开始,机器人身上没有安装任何传感器,此时你给机器人一个目标,让它跑到距离它当前位置 10 米远的前方,因为机器人没有环境传感器,即缺乏反馈信息,它在前进时,很可能就会偏离当前目标,如图 1 所示:
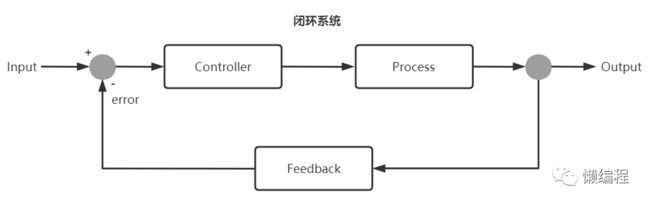
图 1将开环系统的整体结构抽象一下,如图 2 所示:
图 2结合机器人的例子,其中:
Input:机器人接收到一个指令,该指令让机器人前进 10 米
Controller:控制器通过计算得出要前进的方向与距离
Process:机器人执行控制器的计算结果,前进相应的距离
从图 2 可以看出,整个系统是没有反馈的,此时机器人在前进的过程中,很可能就出现图 1 的情况。
我们为机器人添加环境传感器,它现在可以判断自己与目标的方向与距离的,此时,我们将开环系统转变成了闭环系统,其抽象结构为:
图 3在闭环系统中,机器人的例子是这样的:
Input:机器人接收到一个指令,该指令让机器人前进 10 米
Controller:控制器通过计算得出要前进的方向与距离
Process:机器人执行控制器的计算结果,前进相应的距离
Feedback:传感器收集环境信息,比如当前是否偏离了目标,如果偏离了,就将偏离的距离作为 error ,然后再作为 Controller 输入的一部分
在闭环系统下,机器人可以比较好的到达目标位置了,但如果要求机器人尽可能快的到达目标位置呢?
尽可能快背后的要求是,完成任务的时间尽可能短且要准确的到达目的地,不能有偏差,此时我们可以利用 PID 算法去实现这个目标。在闭环系统中,主要就是利用 PID 算法来实现了 Controller 这块,如图 4 所示:
图 4理解 PID 算法思想
举一个经典的例子。
我有一个水缸,希望让水缸中的水位保持在 1 米。
假设现在水缸中,其水位为 0.2 米,此时误差(error)为 0.8 米(1-0.2)。
我知道误差为 0.8 后,开始往水缸里加水,目标是让水缸中的水保持在 1 米。
回到 PID 算法,其中的 P(Proportion)表示比例控制,我们将 PID 算法简化成 P 算法(其不考虑 ID 部分的算法逻辑),其公式为:,其中 表示 时刻下当前的水位, 表示 时刻下当前的误差,而 是个超参数,是需要人通过试验效果来设置的,即我对 K_p 取不同的值,选择一个效果好的,这里设 ,那么在 时,,即这一次操作,我向水缸里添加了 0.4 米的水,现在水缸里的水位是 0.6 米(0.2+0.4),此时误差是 0.4 米(1-0.6),当 时,我再次加水,计算过程为 ,我向水缸里,添加 0.2 米的水,水缸总水量为 0.8 米(0.6+0.2),一直重复这个过程,就可以让水缸里的水保持在 1 米。
整个过程,只有 是我们按经验设置的,其中 的值越大,水缸到达 1 米的过程就越快,比如设 ,那么 ,此时在 的时刻,水缸里的水就加到 1 米了,反之 的越小,到达目标的速度就越慢。
PID 算法,似乎只有 P 算法就可以完成的很好,为啥还要 ID 部分的算法呢?
这是因为现实情况中,这个水缸是会漏水的,接着看这个例子。
依旧假设 ,当水缸里的水有 0.8 米时,计算过程为 ,即我要向水缸里加 0.1 米的水,但水缸每 t 时间段下会漏下 0.1 米的水,即我添加完 0.1 米的水后,因为又漏掉了,此时误差还是 0.2 米,然后因为 P 方法,我还会继续往里加 0.1 米的水,这个过程一直反复,但水缸里的水位将固定在 0.8 米,不再变化。
这种情况便是:稳态误差,顾名思义,误差不会在变小。
在实际生活中,漏水的水缸是存在的,比如通过控制汽车时,会有摩擦阻力(漏水),控制无人机时,会有空气阻力(漏水),各种阻力,都是水缸中漏水的那个口子。
PID 中 I(Integration )算法部分就是为了解决稳态误差的问题,原本的 P 算法加上 I 算法后,其公式为:。
依旧回到水缸的例子,当水位维持 0.8 米时,I 算法会计算出 0 到 t 时刻下误差的积分,误差积分再乘以 这个超参数(也是需要人按具体试验结果进行设置),I 算法获得的值添加到 P 算法中,此时水缸漏水是 0.1 米,而 PI 算法共同计算出的值会大于 0.1 米,水缸水位会慢慢上升到 1 米。
现在还剩 PID 算法中的 D(Differentiation)算法,在实际使用时,D 算法确实是按需使用的,即不用 D 算法,也是常规操作。
D 算法主要的作用就是减少系统在到达目标过程中产生的大量震动,依旧以水缸为例,通过 D 算法,可以防止给水缸加水时,超过 1 米的高度,然后减少水位,又低于1米,然后又加水,又超过1米,这种反复震荡的情况,需要注意,震荡通常都会存在,而D算法目标是减少震荡次数,而不是完全消除震荡。
PID 算法公式拆解
个人认为,深入理解 PID 算法的公式,才是掌握 PID 算法的不二法门,虽然前面通过简单的比喻理解了 PID 算法的思想,但还是有必要讨论一下其公式。
先摘抄一下 PID 算法公式:
公式
上述公式中:
:某个时刻
:某个时刻下的误差
:比例增益
:积分增益
:微分增益
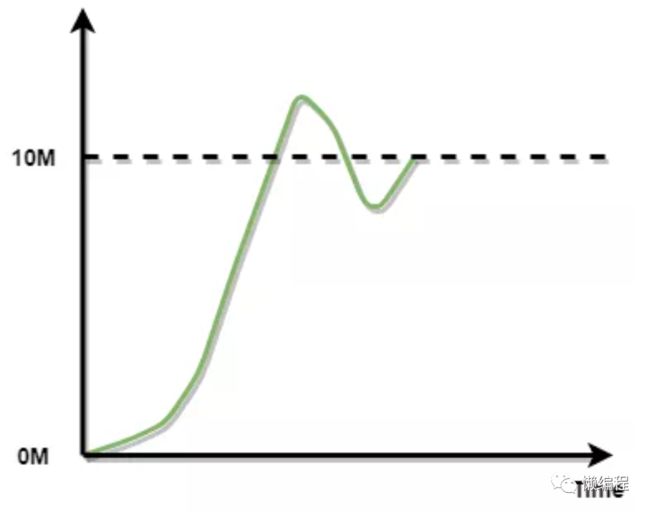
我们以文章一开始提及的,机器人移动到 10 米前的位置为例子,基于 P 算法,机器人从初始位置移动到目标位置时,其距离变化图 5 所示:
图 5可以发现,机器人为了实现尽快到达目标的目的,在一开始距离比较远时,速度在快速加快,从图 5 来看,就是斜率较大的部分,此时机器人快速到达 10M 处,但是因为速度问题,冲过了 10 米,冲过后,基于 Feedback 的误差,机器人将会往回走,经过几次波动后,到达 10 米的目标位置。
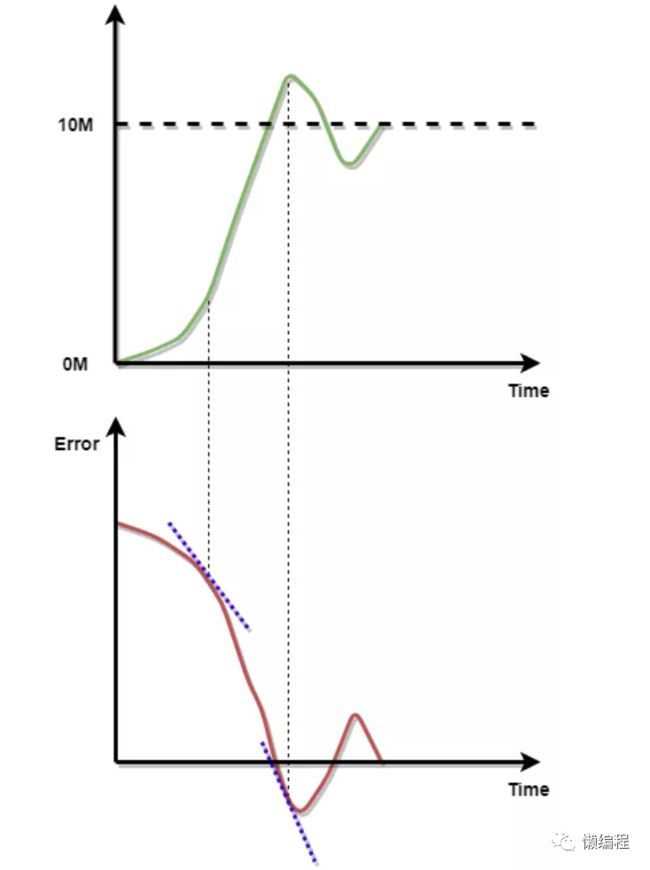
我们将机器人移动过程中,误差变化所对应的函数 也绘制出来,如下图 6 所示:
图 6从图 6 可以看出,P 算法 会基于误差控制机器人移动速度,在第一个虚线处,error 较大且是正数,P 算法会让机器人快速移动,第二虚线处,error 是负数,P 算法会让机器人往回移动。
I 算法()表示误差在一定时间内的积分,通过图画出来,积分就是 函数曲线与 Time 轴之间的面积,如图 7 所示:
图 7I 算法通过积分算法,不断积累误差(面积一直在变大),最终乘以 ,便是 I 算法的部分。
D 算法()是误差的微分处理,它表示 函数在某一点的斜率,如图 8 所示:
图 8从图 8 可知,当斜率变化过快时,D 算法便会获得较大的负数,以抑制输出的上升速度,从而避免机器人在到达目标时,多次震荡。
PID 算法中3 个不同部分相互配合,其直观形式如下 gif 图:
离散化处理
在数字系统中使用 PID 算法时,因为数字系统是离散的(只有 0 和 1),所以我们需要对 PID 算法进行离散化处理,这里的公式变化需要微积分相关的知识。
设系统采样的时间段为 ,将系统获得的误差 序列化为 ,即 时间段下,可以获得 n 个独立的误差,输出也需要由 变化成 .
对于其中第 k 个 () 输出,其公式如下:
公式
(如果不理解,可以尝试从几何角度画图理解一下。)
Python 实现
利用 Python,基于 PID 离散化公式形式,实现 PID 算法,代码如下(代码中给出了关键注释):
import time
class PID:
"""
PID算法实现
"""
def __init__(self, P=0.2, I=0.0, D=0.0, current_time=None):
"""
:param P: P算法超参数
:param I: I算法超参数
:param D: D算法超参数
:param current_time: 当前时刻
"""
self.Kp = P
self.Ki = I
self.Kd = D
# 采样时间段
self.sample_time = 0.00
self.current_time = current_time if current_time is not None else time.time()
self.last_time = self.current_time
self.clear()
def clear(self):
"""
清理系数
"""
self.SetPoint = 0.0
self.PTerm = 0.0
self.ITerm = 0.0
self.DTerm = 0.0
self.last_error = 0.0
self.int_error = 0.0
# 最大的波动值
self.I_max_modify = 20.0
self.output = 0.0
def update(self, feedback_value, current_time=None):
"""
math::
u(k) = K_pe_k + K_i\sum_{j=0}^ke(j)\Delta t + K_d\frac{e(k) - e(k-1)}{\Delta t}
"""
# 误差
error = self.SetPoint - feedback_value
self.current_time = current_time if current_time is not None else time.time()
# 间隔时间
delta_time = self.current_time - self.last_time
if(delta_time >= self.sample_time):
self.ITerm += error * delta_time
# 限制积分项ITerm最大与最小值
if(self.ITerm < -self.I_max_modify):
self.ITerm = -self.I_max_modify
elif(self.ITerm > self.I_max_modify):
self.ITerm = self.I_max_modify
self.DTerm = 0.0
if delta_time > 0:
self.DTerm = (error - self.last_error) / delta_time
# 更新时间
self.last_time = self.current_time
self.last_error = error
# PID结果
self.output = (self.Kp * error) + (self.Ki * self.ITerm) + (self.Kd * self.DTerm)为了判断写的代码是否正确,这里再写一个简单的测试代码,如下:
from pid import PID
import time
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import BSpline, make_interp_spline
def test_pid():
# PID中的超参数
P = 1.2
I = 1
D = 0.001
# 循环次数
L = 50
pid = PID(P, I, D)
pid.SetPoint = 0.0
pid.sample_time = 0.01
feedback = 0
feedback_list = []
time_list = []
setpoint_list = []
for i in range(1, L):
pid.update(feedback)
output = pid.output
if pid.SetPoint > 0:
# 更新feedback
feedback += (output - (1/i))
# 目前只是为了观察
if i > 9:
pid.SetPoint = 1
if i > 30:
pid.SetPoint = 1.2
time.sleep(0.02)
# 为了绘制曲线,记录相应的数值
feedback_list.append(feedback)
setpoint_list.append(pid.SetPoint)
time_list.append(i)
time_sm = np.array(time_list)
# 在指定的间隔内返回均匀间隔的数字
time_smooth = np.linspace(time_sm.min(), time_sm.max(), 300)
# 拟合一条曲线 - 拟合后,曲线才能绘制出来
feedback_smooth = make_interp_spline(time_list, feedback_list)(time_smooth)
plt.plot(time_smooth, feedback_smooth, color='r')
# 拟合目标变化句
plt.plot(time_list, setpoint_list, color='b')
plt.xlim((0, L))
plt.ylim((min(feedback_list)-0.5, max(feedback_list)+0.5))
plt.xlabel('time (s)')
plt.ylabel('PID')
plt.title('TEST PID')
plt.ylim((1-0.5, 1+0.5))
plt.grid(True)
plt.show()
if __name__ == "__main__":
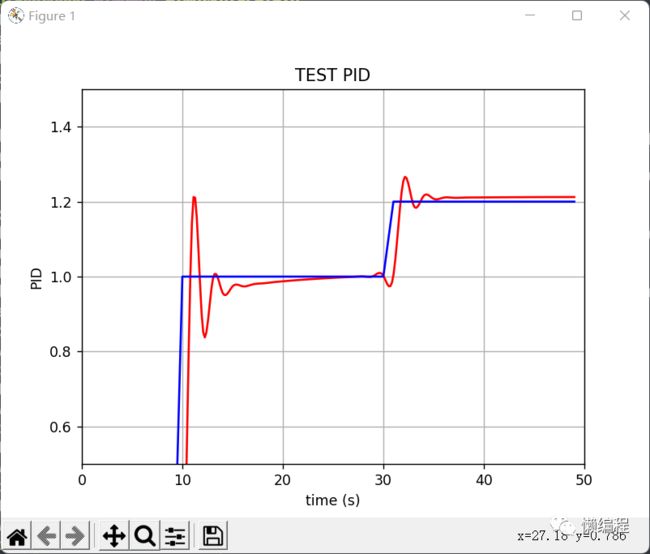
test_pid()为了方便观察,循环 i>9 时,才将目标设置为 1,然后当 i>30 时,将目标修改为 1.2,然后将 PID 算法的结果通过曲线图绘制出来,从而直观的看出,我们实现的 PID 算法,其效果如何,最终效果如下:
从上图可以看出,效果还不错 o (>_<) o
那么关于 PID 算法,就简单讨论到这里,我是二两,我们下篇文章见。