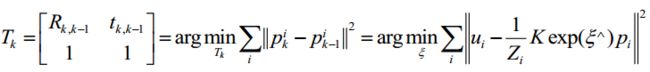【SLAM模块】多视图几何 - 运动估计
[SLAM模块] 多视图几何 - 运动估计
运动估计
运动估计指根据特征点的匹配情况,恢复出两帧间的相机运动,即解算出旋转矩阵R和平移向量t。
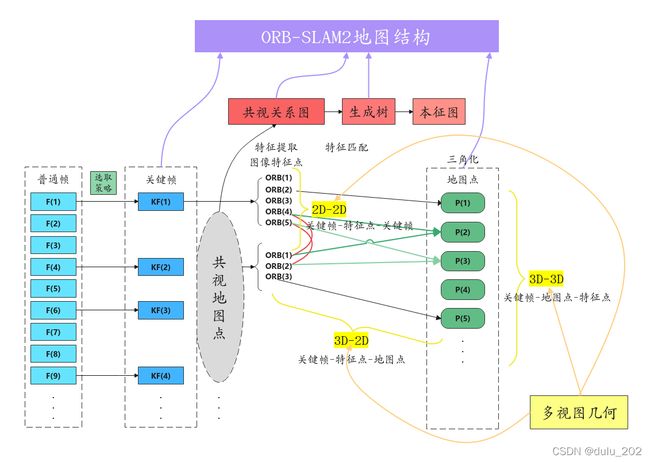
针对特征点匹配的情况,运动估计可分为 2D-2D、3D-2D、3D-3D 三种模型,即多视图几何模型。
其求解方法可以分为几何方法和优化方法。
几何方法:主要是根据对极几何理论得到两帧间的对应关系。
p 2 T K − T t ^ R K − 1 p 1 = p 2 T K − T E K − 1 p 1 = P 2 T E P 1 = p 2 T F p 1 = 0 \mathbf{p}_{2}^{T}\mathbf{K}^{-T}\hat{t}R\mathbf{K}^{-1}\mathbf{p}_{1} =\mathbf{p}_{2}^{T}\mathbf{K}^{-T}E\mathbf{K}^{-1}\mathbf{p}_{1} = \mathbf{P}_{2}^{T}E\mathbf{P}_{1} =\mathbf{p}_{2}^{T}F\mathbf{p}_{1} =0 p2TK−Tt^RK−1p1=p2TK−TEK−1p1=P2TEP1=p2TFp1=0
E = t ^ R E = \hat{t}R E=t^R, F = K − T E K − 1 F = \mathbf{K}^ {-T}E\mathbf{K}^{-1} F=K−TEK−1
优化方法:主要是构建两帧间的重投影误差并使其最小,从而得到帧间变换矩阵。
多视图几何
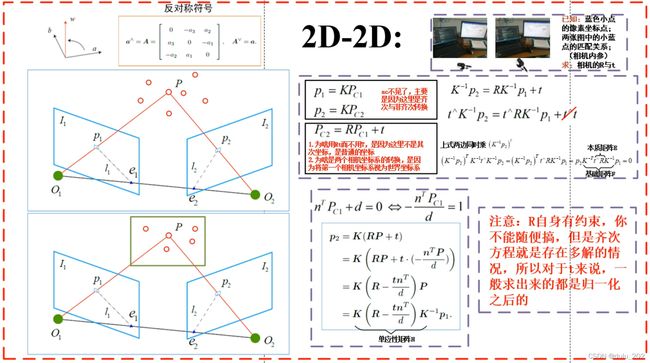
2D-2D
2D-2D 主要是针对单目相机的初始化过程,在不知道空间中3D点的情况下(如未进行初始化)通过两帧间匹配的特征点进行帧间相机运动估计。
涉及到对极几何中基础矩阵(F),本质矩阵(E)或单应性矩阵(H)的相关理论及其分解,通常在图像的特征匹配中难免会有“外点”,可以采用随机采样一致(RANSAC)得到最大“内点”子集的 E 或 H。
F的分解
F = K − T E K − 1 F = \mathbf{K}^ {-T}E\mathbf{K}^{-1} F=K−TEK−1
// 计算基础矩阵
Mat fundamental_matrix;
fundamental_matrix = findFundamentalMat(img_1_points, img_2_points, CV_FM_8POINT);
cout << "-- fundamental_matrix is " << endl << fundamental_matrix << endl;
E的分解(3x3)
E = t ^ R E = \hat{t}R E=t^R,E的自由度为5,8点法求解,奇异值SVD分解恢复出相机的运动R,t,有四个可能的解,但只有一个深度为正。根据线性方程接出来的E,可能不满足E的内在性质-它的奇异值不一定为特定的形式。
// 计算本质矩阵
Point2d principal_point(325.1, 249.7); //相机焦点
int focal_length = 521; //相机焦距
Mat essential_matrix;
essential_matrix = findEssentialMat(img_1_points, img_2_points, focal_length, principal_point);
cout << "-- essential_matrix = " << endl << essential_matrix << endl;
// 从本质矩阵中恢复旋转和平移信息.
recoverPose(essential_matrix, img_1_points, img_2_points, R, t, focal_length, principal_point);
cout << "-- R = " << endl << R << endl;
cout << "-- t = " << endl << t << endl;
H的分解(9x9)
H的自由度为8,描述的是两个平面间的运动关系,当特征点都集中在同一个平面上,则通过单应性来进行运动估计。H可以用四组(每三组不共线)匹配特征点采用直接线性变换法(DLT)算出。通过数值法和解析法分解得到相应的旋转矩阵R和平移向量t以及n、d、k,返回四组进行8选1。
// 计算单应矩阵
Mat homography_matrix;
homography_matrix = findHomography(img_1_points, img_2_points, RANSAC, 3);
cout << "-- homography_matrix = " << endl << homography_matrix << endl;
存在的问题
-
单目视觉的尺度不确定性
对t进行归一化;令初始化时所有的特征点平均深度为1;固定一个尺度 -
初始化的纯旋转问题
单目初始化不能只有纯旋转,必须有一定程度的平移。如果相机发生纯旋转,会导致t为零,得到的E也为零,这将导致无法求解R。 -
多于8对点的情况
工程中给定的点数多于8对,可以计算一个最小二乘解。方程构成一个超定方程,可以通过最小化一个二次型来求。 -
存在误匹配的情况
使用随机采样一致性(RANSAC)来求,适用于很多带错误数据的情况,可以处理带有错误匹配的数据。RANSAC 随机采样一致,RANSAC主要解决样本中的外点问题,可以去除错误匹配,最多可处理50%的外点情况。 RANSAC通过反复选择数据中的一组随机子集来达成目标。被选取的子集被假设为局内点,并用下述方法进行验证: N — 样本点个数, K — 求解模型需要最少的点的个数 1. 随机采样K个点 2. 对该K个点拟合模型 3. 计算其它点到拟合模型的距离,小于一定阈值,当作内点,统计内点个数 4. 重复M次,选择内点数最多的模型 5. 利用所有的内点重新估计模型(可选)
三角测量
定义:得到运动R,t后,求解特征点的空间3D位置、估计地图点的深度。
方法:左乘后,先求s2再求s1,由于噪声的存在,更常见的是求最小二乘解而不是零解。
问题:解得深度的质量与平移相关,平移较大时,在同样的相机分辨率下,三角化测量将更精确,但是平移大时特征匹配可能不成功,而平移较小,三角化精度不够。
// 1. projMatr1:第一个相机位姿(4x3的矩阵)
// 2. projMatr2:第二个相机位姿(4x3的矩阵)
// 3. projPoints1:第一个相机坐标系下的特征点坐标
// 4. projPoints2:第二个相机坐标系下的特征点坐标
void triangulatePoints(InputArray projMatr1,
InputArray projMatr2,
InputArray projPoints1,
InputArray projPoints2,
OutputArray points4D)
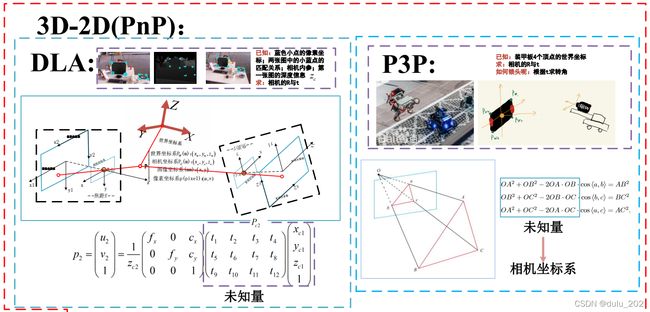
3D-2D
PnP(perspective-n-point)就是求解 3D 到 2D 点对运动的方法,描述的是当知道N个3D空间点(三角测量得出的地图点)及其投影位置时(例如单目,已经初始化完毕,知道特征点的3D位置),如何估计相机位姿。
通俗的讲,PnP问题就是在已知世界坐标系下N个空间点的真实坐标以及这些空间点在图像上的投影,如何计算相机所在的位姿。
已知量是空间点的真实坐标和图像坐标,未知量(求解量)是相机的位姿。
双目或者深度相机可以直接使用PnP。对PnP的求解有 DLT、 P3P、EPnP、 UPnP以及非线性优化方法。现在常用的做法是先采用 P3P 得到初始解,然后构建重投影误差,使之最小化。使用李代数上的扰动模型分析其导数,并通过高斯牛顿等优化方法得到两帧间的相对变换,具体做法又叫作捆集优化(bundle adjustment, BA),在编程上一般采用General Graph Optimization(G2O) 等优化库实现。
代数解法
DLT
直接线性变换,直接构建一个12个未知数的 [R|t] 增广矩阵(先不考虑旋转矩阵的自由度只有3),因此最少通过6对匹配点即可实现对矩阵 [R|t] 12个未知数的线性求解(每一个3D点到归一化平面的映射给出两个约束)。当匹配点大于6对时,也可以使用SVD等方法对超定方程求最小二乘解。对于旋转矩阵R,必须针对DLT估计的T左边3x3的矩阵块,寻找一个最好的旋转矩阵对它进行近似(将3x3矩阵空间投影到SE(3)流形上),使用QR分解完成。
P3P
仅使用3对匹配点,还需要一对验证点,以从可能的解中选出正确的那一个,对数据要求较少。一旦3D点在相机坐标系下的坐标能够算出,就能够得到3D-3D的对应点,把PnP问题转换为ICP问题。利用三角形相似性质,求解投影点a、b、c在相机坐标系下的3D坐标,最后把问题转换成一个3D到3D的位姿估计问题。
缺点:
-
P3P只利用3个点的信息,当给定的配对点多于3组时,难以利用更多的信息。
-
如果3D点或2D点受噪声影响,或者存在误匹配,则算法失效。
EPnP
需要4对不共面的(对于共面的情况只需要3对)3D-2D匹配点,是目前最有效的PnP求解方法。
空间中任意3D点的坐标可以用4个不共面的3D点坐标的权重表示。
从地图点中选出4个控制点 c 1 \mathbf{c}_{1} c1、 c 2 \mathbf{c}_{2} c2、 c 3 \mathbf{c}_{3} c3、 c 4 \mathbf{c}_{4} c4以及1个对应的参考点 p i \mathbf{p}_{i} pi,4个控制点与1个参考点通过加权和的方式关联。
利用控制点和参考点的加权关系在世界坐标系和相机坐标系中不变的性质,通过构造投影点的投影方程,但方程又不直接求参考点的坐标,而是巧妙地运用参考点和控制点的加权和关系间接求出控制点的坐标,即求出地图点在相机坐标系下的坐标值,然后利用ICP算法找到地图点在世界坐标系与相机坐标系的变换关系求位姿。
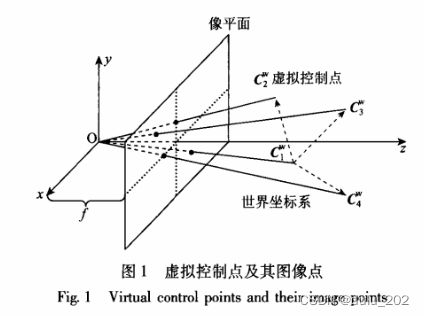
通常选取世界坐标下的四个控制点坐标为 C w = [ 0 , 0 , 0 , 1 ] T , [ 1 , 0 , 0 , 1 ] T , [ 0 , 1 , 0 , 1 ] T , [ 0 , 0 , 1 , 1 ] T Cw = \mathbf{[0,0,0,1]}^{T},\mathbf{[1,0,0,1]}^{T},\mathbf{[0,1,0,1]}^{T},\mathbf{[0,0,1,1]}^{T} Cw=[0,0,0,1]T,[1,0,0,1]T,[0,1,0,1]T,[0,0,1,1]T ;通过 n 个 3D 点在相机平面的投影关系,以及与这四个控制点的权重关系,构建一个12x12方阵,求得其零空间特征向量,可以得到虚拟控制点的相机平面坐标,然后使用 POSIT 算法即可求出相机位姿。
通常在用EPnP求得四对点下的封闭解后,可以将该解作为非线性优化的初值,优化提高精度。
// 1. objectPoints - 世界坐标系下的控制点的坐标,在这里可以使用vector的数据类型
// 2. imagePoints - 图像坐标系下对应的控制点的坐标,在这里可以使用vector的数据类型
// 3. cameraMatrix - 相机的内参矩阵
// 4. distCoeffs - 相机的畸变系数
// 5. rvec - 输出的旋转向量,使坐标点从世界坐标系旋转到相机坐标系
// 6. tvec - 输出的平移向量,使坐标点从世界坐标系平移到相机坐标系
// 7. flags - 默认使用CV_ITERATIV迭代法
void solvePnP(InputArray objectPoints,
InputArray imagePoints,
InputArray cameraMatrix,
InputArray distCoeffs,
OutputArray rvec,
OutputArray tvec,
bool useExtrinsicGuess=false,
int flags = CV_ITERATIVE)
// 1. _opoints 参考点在世界坐标系下的点集;float or double
// 2. _ipoints 参考点在相机像平面的坐标;float or double
// 3. _cameraMatrix 相机内参
// 4. _distCoeffs 相机畸变系数
// 5. _rvec 旋转矩阵
// 6. _tvec 平移向量
// 7. useExtrinsicGuess 若果求解PnP使用迭代算法,初始值可以使用猜测的初始值(true),也可以使用解析求解的结果作为初始值(false)。
// 8. iterationsCount Ransac算法的迭代次数,这只是初始值,根据估计外点的概率,可以进一步缩小迭代次数;(此值函数内部是会不断改变的),所以一开始可以赋一个大的值。
// 9. reprojectionErrr Ransac筛选内点和外点的距离阈值,这个根据估计内点的概率和每个点的均方差(假设误差按照高斯分布)可以计算出此阈值。
// 10. confidence 此值与计算采样(迭代)次数有关。此值代表从n个样本中取s个点,N次采样可以使s个点全为内点的概率。
// 11. _inliers 返回内点的序列。为矩阵形式
// 12. flags 最小子集的计算模型;
// SOLVEPNP_ITERATIVE(此方案,最小模型用的EPNP,内点选出之后用了一个迭代);
// SOLVE_P3P(P3P只用在最小模型上,内点选出之后用了一个EPNP)
// SOLVE_AP3P(AP3P只用在最小模型上,内点选出之后用了一个EPNP)
// SOLVE_EPnP(最小模型上&内点选出之后都采用了EPNP)
// 返回值: 成功返回true,失败返回false;
bool solvePnPRansac(InputArray _opoints,
InputArray _ipoints,
InputArray _cameraMatrix,
InputArray _distCoeffs,
OutputArray _rvec,
OutputArray _tvec,
bool useExtrinsicGuess = false,
int iterationsCount = 100,
float reprojectionError = 8.0,
double confidence = 0.99,
OutputArray _inliers = noArray(),
int flags = SOLVEPNP_ITERATIVE)
通常解法
在SLAM中,通常的做法是先使用P3P/EPnP等方法估计相机位姿,然后构建最小二乘问题对估计值进行调整。先采用P3P得到初始解,然后构建重投影误差,使之最小化。
优化解法
BA
把PnP问题构建成一个定义于李代数上的非线性最小二乘问题,把相机位姿和空间点位置放在一起优化,最小化重投影误差。
重投影误差
在计算机视觉中,经常会用到重投影误差(Reprojection error)。比如在计算平面单应矩阵和投影矩阵的时候,往往会使用重投影误差来构造代价函数,然后最小化这个代价函数,以优化单应矩阵或者投影矩阵。之所以使用重投影误差,是因为它不光考虑了单应矩阵的计算误差,也考虑了图像点的测量误差,所以其精度会更高。
最小化重投影误差问题(Bundle Adjustment问题)— 可以将位姿T 和三维特征点 P 同时优化
如下图所示,我们通过特征匹配知道,观测值 P1 和 P2 是同一个空间点 P 的投影,P 的投影 P2’ 与观测值 P2 之间有一定的距离,也就是重投影误差。于是我们调整相机的位姿 T, 使这个距离变小,由于这个调整需要考虑很多个点,所以最后每个点的误差通常不会精确到0。
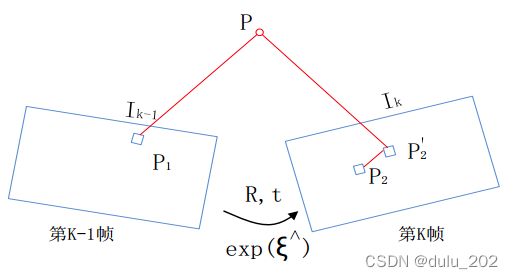
考虑到 n n n 个三维空间点 P P P 和它们的投影点 p p p,**我们希望计算位姿 T T T,用李代数表示为 ** ξ \xi ξ。假设某空间点 P i = [ X i , Y i , Z i ] T \mathbf{P}_{i} = \mathbf{[\mathbf{X}_{i}, \mathbf{Y}_{i}, \mathbf{Z}_{i}]}^{T} Pi=[Xi,Yi,Zi]T,其投影的像素坐标 u i = [ u i , v i ] T \mathbf{u}_{i} = \mathbf{[\mathbf{u}_{i}, \mathbf{v}_{i}]}^{T} ui=[ui,vi]T。
写成矩阵形式就是: s i u i = K e x p ( ξ ) P i \mathbf{s}_{i}\mathbf{u}_{i} = Kexp(\xi)\mathbf{P}_{i} siui=Kexp(ξ)Pi
由于相机位姿未知以及观测点的噪声,该等式存在一个误差。我们将误差求和,构建最小二乘问题,然后寻找做好的相机位姿,使它最小化:

用高斯牛顿法/列文伯格-马夸尔特方法求解。
总结:
在SLAM中优化求解相机运动位姿时(3D-2D),会用到重投影误差,重投影误差是将像素坐标(观测到的投影位置)P2 与3D点 P 按照当前估计的位姿 T 进行投影得到位置 P2’ 相比较得到的误差。然后使用李代数上的扰动模型分析其导数,并通过高斯牛顿等优化方法得到两帧间的相对变换。
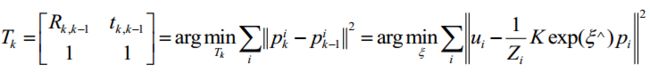
//todo 顶点重置函数
virtual void setToOriginImpl() override{
_estimate = Sophus::SE3d();
}
//todo 顶点更新函数
//! 顶点的更新通过内置的oplusImpl函数实现更新
virtual void oplusImpl(const double *update) override{
Eigen::Matrix update_se3;
update_se3 << update[0], update[1], update[2], update[3], update[4], update[5];
_estimate = Sophus::SE3d::exp(update_se3) * _estimate;
}
//todo 边的误差计算函数
virtual void computeError() override{
//* error = ui - 1/Zi * K * T * Pi
const VertexPose *v = static_cast(_vertices[0]); //^ 顶点
Sophus::SE3d T = v->estimate(); //^ 待估计参数
Eigen::Vector3d pos_pixel = _K * (T * _pos3d); // 将3D地图点按照当前的位姿T进行投影得到像素点
pos_pixel /= pos_pixel[2]; // 归一化
_error = _measurement - pos_pixel.head<2>();
}
//todo 边计算雅克比矩阵
//! 误差关于顶点的偏导数定义在边里的雅克比矩阵J上
virtual void linearizeOplus() override{
const VertexPose *v = static_cast(_vertices[0]); //^ 顶点
Sophus::SE3d T = v->estimate(); //^ 待估计参数
Eigen::Vector3d pos_cam = T * _pos3d; // 相机坐标下的地图点
double fx = _K(0, 0);
double fy = _K(1, 1);
double cx = _K(0, 2);
double cy = _K(1, 2);
double X = pos_cam[0];
double Y = pos_cam[1];
double Z = pos_cam[2];
double Z2 = Z * Z;
_jacobianOplusXi
<< -fx / Z, 0, fx * X / Z2, fx * X * Y / Z2, -fx - fx * X * X / Z2, fx * Y / Z,
0, -fy / Z, fy * Y / (Z * Z), fy + fy * Y * Y / Z2, -fy * X * Y / Z2, -fy * X / Z;
}
3D-3D
3D-3D 主要是激光 SLAM 采用迭代最近点(ICP)求解。在 VSLAM 中,可以在 RGB-DSLAM 中使用,但由于 RGB-D相机的限制,仅仅适用室内,而且适用小的场景。这是由于深度的估计不准,导致误差比 3D-2D 大。直观的感觉是, 相机得到的 3D 位置误差较大(相机方向性好, 距离信息误差大), 3D-2D 只使用一次深度信息,但是 3D-3D 采用两次深度信息,导致计算的精确度降低,所以在普通相机中一般回避 3D-3D 的方式。
代数解法
定义第i对点的误差项: e i = p i − ( R p i ′ + t ) \mathbf{e}_{i}=\mathbf{p}_{i} - (R\mathbf{p}_{i}^{'}+t) ei=pi−(Rpi′+t)
构建最小二乘问题,求使误差平方和达到最小值的 R , t R,t R,t: m i n R , t 1 2 ∑ i = 1 n ∣ ∣ ( p i − ( R p i ′ + t ) ) ∣ ∣ 2 2 \underset{R,t} {min} \frac{1}{2}\sum\limits_{i=1}^{n}\mathbf{||(\mathbf{p}_{i} - (R\mathbf{p}_{i}^ {'}+t))||}^{2}_{2} R,tmin21i=1∑n∣∣(pi−(Rpi′+t))∣∣22
ICP求解步骤
1. 计算两组点的质心位置p,p':
p = 1 n ∑ i = 1 n ( p i ) p = \frac{1}{n}\sum\limits_{i=1}^{n}(\mathbf{p}_{i}) p=n1i=1∑n(pi) , p ′ = 1 n ∑ i = 1 n ( p i ′ ) p' = \frac{1}{n}\sum\limits_{i=1}^{n}(\mathbf{p}_{i}^{'}) p′=n1i=1∑n(pi′)
Point3f p1, p2;
int N = pts1.size();
for(int i = 0; i < N; i++){
p1 += pts1[i];
p2 += pts2[i];
}
p1 = Point3f(Vec3f(p1) / N);
p2 = Point3f(Vec3f(p2) / N);
2. 计算每个点的去质心坐标:
q i = p i − p \mathbf{q}_{i} = \mathbf{p}_{i} - p qi=pi−p, q i ′ = p i ′ − p ′ \mathbf{q}_{i}^{'} = \mathbf{p}_{i}^{'} - \mathbf{p}^{'} qi′=pi′−p′
vector q1(N), q2(N);
for(int i = 0; i < N; i++){
q1[i] = pts1[i] - p1;
q2[i] = pts2[i] - p2;
}
3. 根据以下优化问题计算旋转矩阵:
R ∗ = arg m i n R 1 2 ∑ i = 1 n ∣ ∣ q i − R q i ′ ∣ ∣ 2 \mathbf{R}_{*} = \arg \underset{R} {min} \frac{1}{2}\sum\limits_{i=1}^{n}\mathbf{||\mathbf{q}_{i} - R\mathbf{q}_{i}^{'}||}^{2} R∗=argRmin21i=1∑n∣∣qi−Rqi′∣∣2
SVD求解R
3.1 定义矩阵W
W = ∑ i = 1 n q i q i ′ T W = \sum\limits_{i=1}^{n}\mathbf{q}_{i}\mathbf{q}_{i}^{'T} W=i=1∑nqiqi′T
Eigen::Matrix3d W = Eigen::Matrix3d::Zero();
for(int i = 0; i < N; i++){
W += Eigen::Vector3d(q1[i].x, q1[i].y, q1[i].z) * Eigen::Vector3d(q2[i].x, q2[i].y, q2[i].z).transpose();
}
3.2 对W进行SVD分解(W是一个3x3的矩阵)
W = u ε v T W = u\varepsilon\mathbf{v}^{T} W=uεvT
Eigen::JacobiSVD svd(W, Eigen::ComputeFullU | Eigen::ComputeFullV);
Eigen::Matrix3d U = svd.matrixU();
Eigen::Matrix3d V = svd.matrixV();
3.3 W满秩时,R为(其中U和V为对角矩阵)
R = u v T R = u\mathbf{v}^{T} R=uvT
如果此时R的行列式为负,则取-R作为最优值。
Eigen::Matrix3d R_ = U * (V.transpose());
if (R_.determinant() < 0) {
R_ = -R_;
}
4. 根据R计算t:
t ∗ = p − R p ′ \mathbf{t}_{*} = p-Rp' t∗=p−Rp′
Eigen::Vector3d t_ = Eigen::Vector3d(p1.x, p1.y, p1.z) - R_ * Eigen::Vector3d(p2.x, p2.y, p2.z);
非线性优化解法
以迭代的方式去找最优解
构建最小二乘问题,求使误差平方和达到最小值的 R , t R,t R,t: m i n R , t 1 2 ∑ i = 1 n ∣ ∣ ( p i − ( R p i ′ + t ) ) ∣ ∣ 2 2 \underset{R,t} {min} \frac{1}{2}\sum\limits_{i=1}^{n}\mathbf{||(\mathbf{p}_{i} - (R\mathbf{p}_{i}^ {'}+t))||}^{2}_{2} R,tmin21i=1∑n∣∣(pi−(Rpi′+t))∣∣22
//todo 顶点重置函数
//! 设置初始值
virtual void setToOriginImpl() override{
_estimate = Sophus::SE3d();
}
//todo 顶点更新函数
//! 更新方式
//! 顶点的更新通过内置的oplusImpl函数实现更新
virtual void oplusImpl(const double *update) override{
Eigen::Matrix update_se3;
update_se3 << update[0], update[1], update[2], update[3], update[4], update[5];
_estimate = Sophus::SE3d::exp(update_se3) * _estimate;
}
// 误差计算函数
virtual void computeError() override{
//* error = pi - T * Pi'
const VertexPose *v = static_cast(_vertices[0]); //^ 顶点
Sophus::SE3d T = v->estimate(); //^ 待估计参数
_error = _measurement - T * _point;
}
// 计算雅克比矩阵
//! 误差关于顶点的偏导数定义在边里的雅克比矩阵J上
virtual void linearizeOplus() override{
const VertexPose *v = static_cast(_vertices[0]); //^ 顶点
Sophus::SE3d T = v->estimate(); //^ 待估计参数
Eigen::Vector3d xyz_trans = T * _point;
_jacobianOplusXi.block<3, 3>(0, 0) = -Eigen::Matrix3d::Identity();
_jacobianOplusXi.block<3, 3>(0, 3) = Sophus::SO3d::hat(xyz_trans); //* 为向量到反对称矩阵
}
在唯一解的情况下,只要能找到极小值解,那么这个极小值就是全局最优值,不会出现局部极小而非全局最小的情况。ICP求解可以任意选定初始值,这是已知匹配点时求解ICP的一大好处。在激光情况下,匹配点未知,将指定最近点为匹配点,此时问题非凸,极小值不一定为最小值。
可以混合使用PnP和ICP优化,对于深度已知的特征点,建模它们的3D-3D误差;对于深度未知的特征点,则建模2D-3D的重投影误差,于是,可以将所有的误差放在同一个问题中考虑。
IterativeClosestPoint icp;
// 设置输入点云和目标点云
icp.setInputCloud (cloud_source);
icp.setInputTarget (cloud_target);
// 设置最大对应距离为5cm(超过距离阈值的对应关系将被忽略)
icp.setMaxCorrespondenceDistance (0.05);
// 设置最大迭代次数(标准 1)
icp.setMaximumIterations (50);
// 设置两次变换矩阵之间的差值 (标准 2)
icp.setTransformationEpsilon (1e-8);
// 设置均方误差 (标准 3)
icp.setEuclideanFitnessEpsilon (1);
// 执行对齐
icp.align (cloud_source_registered);
// 获取目标点云与注册的目标点云一致的转换
Eigen::Matrix4f transformation = icp.getFinalTransformation ();
文中代码gitee链接:https://gitee.com/neu-real-lxj/slam_-moudle/tree/master/slam_moudle
视觉SLAM的一些模块实现,包括特征提取、特征匹配、三角化、点云配准、VO、相关库的操作等,本文的具体代码都在其中,希望点个小心心,谢谢!
感谢沈航洪恺临老哥的SLAM讲解视频,受益匪浅,文中2D-2D,3D-2D的图片摘自老哥的visio,视频链接:https://www.bilibili.com/video/BV1Rh411o7Jb?spm_id_from=333.999.0.0