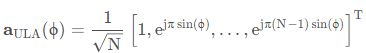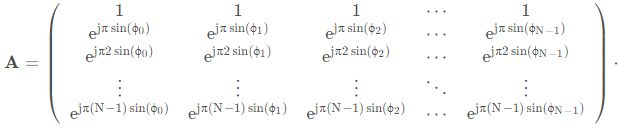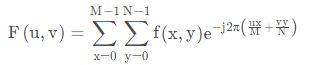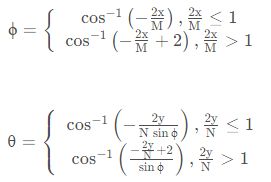MIMO信道估计中的码本

         在MIMO信道估计等问题中， 往往需要使用码本， 而最常用的就是DFT码本。 本文介绍了为何DFT码本可以如此适用于作为信道估计的码本。首先会从ULA 阵列天线入手， 然后拓展到UPA 平面天线。

1 DFT矩阵

离散变换（DFT）可以写为：

       （1）

 X [ k ] 代表的是频域第 k个频点的值（响应），x[n] 是时域的第 n个信号, N是总采样数。
我们可以有下式的DFT矩阵F：

                                （2）

由(1)可知：

 

简而言之， 对时域信号左乘DFT矩阵， 即可得到频域信号。

 注意： F是正交矩阵，这个可以通过等比数列求和公式得到。

2 ULA的响应向量

对于共N个天线， 天线间隔为半波长的阵列， 其响应向量可以表示为：

响应向量为 入射角度 ϕ 的函数

3 DFT 码本

那么， 我们可以把 N个不同入射角度对应的响应向量合写在一个矩阵中， 如下：

 （3）

如果我们令 那么比较(2) 和 (3)， 可知A=F.但需要注意: sin ⁡ ( ϕ ) ∈ [-1, 1] 所以有些值是取不到的。 同时也有： 因此，我们应该令，

此时 A = F 仍成立。 同时， 我们可以倒推出所有 

 这里，A 就是基于 DFT矩阵得到的 DFT码本。A 的每一列代表了一个入射角度的对应天线响应。 其最大的特点是， 每一个入射角度的天线响应之间互相正交（DFT矩阵的性质）。码本覆盖了空间0~180度的范围（对应sin值从-1到1），分辨力（最小间隔）为：

     简单总结一下：DFT码本相当于将0-180度的空间， 对应到sin值-1到1的空间。 再将-1到1按等间隔划分N个码字， 即可得到正交的码本。 当然，由于三角函数的性质， 对cos值这样划分也有类似的结论。

 4 使用码本画出空间方向图

通过上面的分析， 我们知道， 其实想生成一个正交码本的核心在于相邻码字间的sin值间隔为2/N即可， 不要求从哪个开始，哪个结束。 因此我们可以把A中的列按从sin值-1到1从小到大排序如下， 此时A仍是正交矩阵：

N = 64;
% columns
t = -1 : 2 / N : (N-1) / N;
% rows
g = 0 :(N-1);
A = exp(1j * pi * g' * t);

这里t中就不会出现超过-1或1的情况， 且对应的弧度制是从小到大顺序排列的， 这样的A 更合适。假设我们的波束成形(不管是发送或是接收）向量为其对应的空间方向图（在空间每个角度上的能量响应）可以表示为：

 5 UPA天线响应

      除了ULA， 实际中平面天线阵列（UPA）的应用更为广泛。 UPA的天线响应则与两个参数相关： 入射水平角 θ和仰角 ϕ. UPA的响应公式可以表示为：

 P 和 Q 代表了UPA共有P行，Q列天线。 对应的UPA建模如图：

图中， 我们以中心的接收端UPA的左下角的天线作为第一行第一列元素。 θ发送UPA（图中右下角的小UPA）投影到xy平面后与x轴的夹角, ϕ是与z轴负半轴的夹角。

 简单理解这个响应公式：由于相位与距离成反比。 那么p行的天线相对于第一行的天线， 与发射UPA的距离是增加的， 那么相位就是减小的。 如果第一行第一列天线的相位我们归一化为1作为初始相位， 那么第p行天线的相位就是一个负值。 而信道H通常被我们写为就是我们想求的UPA天线响应。 但是对于不同的建模方式， 如， 以左上角第一个元素为第一行第一列进行建模， 那么结果就不一样了。 包括对θ和 ϕ 的不同定义，也会使最后的建模结果有所不同。但万变不离齐总，核心都是基于相位与距离成反比这一点上。 

二维DFT

二维DFT的公式如下：

（5）

 其中 u = 0 , … , M − 1 ，v=0,…,N−1.

令

可将其列化为g=vec(G). 同时也可将F列化为f， 那么存在二维DFT矩阵T, 使得 f = Tg。根据(5)式， 可以得到T的第k行第j列的元素如下：（k对应于f的第k个元素， 也就是F的第u行第v列，即第j列对应于g的第j个元素， 也就是G的第x行第y列， 

 T矩阵有两个性质：

           第k行和第k列完全相等。
           列与列，行与行之间均正交。

而第二个性质， 就是我们用来设计正交码本的思路：

二维DFT对应的UPA码本

回顾一下两个式子， 二维DFT矩阵T：

 UPA的响应式子：

 

通过变量代换，可以有：

通过改变x,y的值， 我们就可以得到多个对应不同θ 和ϕ的码字， 且互相之间是正交的。 同样的， 我们有

 加一个2保证使其在[-1,1]范围内。

 假设我们现在有波束成形矩阵W，想获取其在各个角度上的响应， 只需要计算：

 代表了第k个码字（方向）上的响应， 可通过k算出其对应的x和y值。如，k = 2就代表x = 2 , y = 0 (所有数从0开始计算）。
那么:

 需要注意的是， 在求θ的时候， 某个码字有一定概率是不对应一个有意义的θ 。因为时， θ是没有意义的。 但为了正交性， 我们没有舍弃这些无意义的码字。

矩阵的列，只要保证间隔分别是2/M和1/N。

事实上， 我们的目的只是为了设计出的码字能尽量均匀地分割整个角度空间， 并彼此之间互相正交。 而类似DFT的形式， 可以做到这一点。 这一节我们脱离DFT， 仅从ULA， UPA的天线响应本身， 来设计正交的码本。 

 参考：

混合波束成形| MIMO系统的DFT码本_B417科研笔记的博客-CSDN博客_dft码本