代码随想录训练营第4天|LeetCode :24.两两交换链表中的节点 19.删除链表的倒数第N个节点 、 面试题 02.07. 链表相交、 142.环形链表II
参考
代码随想录
题目一:LeetCode 24.两两交换链表中的节点
一、按照自己的思路求解
这个题似乎不难,但是做的时候还是花了一些时间,把自己的思路记录一下。先给出代码,再解释一下:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* swapPairs(ListNode* head) {
//链表为空或者只有一个节点则直接返回
if(head == nullptr || head->next == nullptr) return head;
ListNode* pHead = head->next;
ListNode *cur1,*cur2;
//初始化
ListNode* tmp = head;
while(tmp != nullptr && tmp->next != nullptr)
{
cur1 = tmp;
cur2 = tmp->next;
tmp = cur2->next;
//交换
cur2->next = cur1;
cur1->next = tmp;
if(tmp != nullptr && tmp->next != nullptr)
cur1->next = tmp->next;
}
return pHead;
}
};
这里需要用到三个指针,两个指针cur1和cur2指向要交换的两个节点,tmp指向下一个待交换的两个节点中的第一个节点,这也是单链表的特点,当要改变某一个节点的指向的时候,要先记录一下该节点的下一个节点。
- 先判断链表的长度,链表至少有两个节点才进行交换,否则直接返回
if(head == nullptr || head->next == nullptr) return head;
- 交换后的链表的头节点是确定的,即原来的头节点的下一个节点,先保存头节点
ListNode* pHead = head->next;
- 定义三个指针,并对初始化tmp指针,cur1和cur2不用初始化,在接下来的while循环中每次交换两个节点之前都会根据tmp指针来对cur1和cur2进行赋值
ListNode *cur1,*cur2;
//初始化
ListNode* tmp = head;
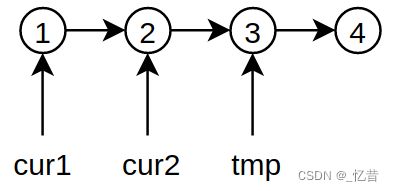
- while循环的开始先赋值cur1和cur2,分别指向两个待交换的两个节点
cur1 = tmp;
cur2 = tmp->next;
tmp = cur2->next;
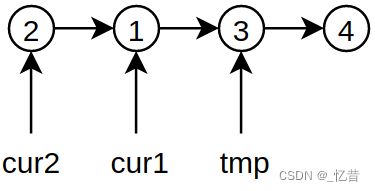
- 交换cur1和cur2指向的节点,交换的结果如下图所示
//交换
cur2->next = cur1;
cur1->next = tmp;
- 如果后面还要继续交换的话,需要先更改当前cur1的下一个节点
if(tmp != nullptr && tmp->next != nullptr)
cur1->next = tmp->next;

这样就可以循环了,当tmp节点为空或者下一个节点为空,那么不再继续交换,所以循环的条件是tmp != nullptr && tmp->next != nullptr。
二、参考代码随想录的实现方法
代码随想录给出的代码如下:
class Solution {
public:
ListNode* swapPairs(ListNode* head) {
ListNode* dummyHead = new ListNode(0); // 设置一个虚拟头结点
dummyHead->next = head; // 将虚拟头结点指向head,这样方面后面做删除操作
ListNode* cur = dummyHead;
while(cur->next != nullptr && cur->next->next != nullptr) {
ListNode* tmp = cur->next; // 记录临时节点
ListNode* tmp1 = cur->next->next->next; // 记录临时节点
cur->next = cur->next->next; // 步骤一
cur->next->next = tmp; // 步骤二
cur->next->next->next = tmp1; // 步骤三
cur = cur->next->next; // cur移动两位,准备下一轮交换
}
return dummyHead->next;
}
};
看了一下,似乎没有特别之处,没有用什么特别的方法,相比之下感觉自己的代码更好理解哈哈。
小结
这个题说难不难,说简单也不简单,做的时候一定要画图理解,涉及到的指针较多,不画图很容易出错。在改变链表中某一个节点的下一个节点时,一定要先保存原来的节点。
题目二:LeetCode 19.删除链表的倒数第N个节点
一、按照自己的想法实现
这个题难点似乎是在倒数上,如果是正数那就是链表的遍历,找到删除的节点,然后删除即可。既然会删除正数的第N个点,那就把倒数转化为正数,问题就解决了。具体做法是先遍历一边链表,得到链表的长度,然后简单相减就可以得到正数的第几个点了。整体来说这个题不难,写完代码也是一次就过,还是挺开心的哈。代码如下:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode* cur = head;
int size = 0;
//遍历链表,获取长度
while(cur != nullptr)
{
cur = cur->next;
size++;
}
//把倒数转化为正数,注意题目中的倒数从1开始,这里的正数从0开始
int index = size - n;
//添加虚拟头节点,方便操作
ListNode* dummyNode = new ListNode(0,head);
//找到要删除的节点的上一个节点
cur = dummyNode;
while(index--) cur = cur->next;
//删除节点
ListNode* tmp = cur->next;
cur->next = cur->next->next;
delete tmp;
head = dummyNode->next;
delete dummyNode;
return head;
}
};
二、参照代码随想录的实现方法
虽然上面自己的方法也能一次通过,但是必须遍历两次。代码思想录给出的方法使用了双指针法。具体做法是让fast指针向移动 n步,然后fast指针和slow指针再一起移动,当fast指针到最后的时候slow指针就指向了要删除节点的上一个节点(之前也一直在强调,删除某一个节点,指针应该指向该节点的上一个节点)。这个实现思路还是非常有启发性的,看了思路之前自己再写一遍:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode* dummyNode = new ListNode(0,head);
ListNode* fast = dummyNode;
ListNode* slow = dummyNode;
int i = n ;
while(i--) fast = fast->next;
while(fast->next != nullptr)
{
fast = fast->next;
slow = slow->next;
}
ListNode* tmp = slow->next;
slow->next = slow->next->next;
delete tmp;
return dummyNode->next;
}
};
小结
本题不用双指针法也能做出来,但是双指针法确实要更优一些,提供另外一种定位倒数节点的方法,只需要遍历一遍就可以了。
题目三:LeetCode 面试题 02.07. 链表相交
一、按照自己的想法实现
这个题也不难,又是一把过哈哈哈,终于直到为啥今天四个题,原来都是简单题。看题目中给出的图,相交部分都是从后面开始的(也只能是这样,如果前面相交再分开,那么最后一个交点指向两个节点?显然不行),而单链表只能从前往后遍历。这题思路还是挺多的,这里说一下我想到的一些方法:
这里补充一个点,一开始以为比较两个节点的值就可以判断是不是同一个节点,但是这种方法是错的,不同的节点也可以有相同的值,所以正确的是比较地址。
- 反转链表。想到这个方法是因为昨天刚做了链表的反转,分别把两个链表反转,然后就可以从前往后遍历,比较每个节点的地址,第一个地址不想等的那两个节点之前的那个节点就是答案。题目中说要保持原来的数据结构,所以如果用这种方法的话需要重新建立两个链表,显得有些复杂
- 既然我们需要从后往前找第一个地址不相等的点,那就可以分别遍历连个链表,把每个节点的地址存储到数组中,然后从后往前遍历数组进行比较就可以了
- 上面第二种方法先将地址放入数组,然后再从后往前遍历,根据这个顺序就很容易可以想到用栈来代替数组,因为我们需要的就是先进后出。这种方法的思想和第二种一种,只是用栈来替代数组
上面三种比较起来,第三种比较容易,代码实现如下:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
if(headA == nullptr || headB == nullptr) return nullptr;
stack<ListNode*> stack1,stack2;
ListNode* cur1 = headA;
ListNode* cur2 = headB;
while(cur1 != nullptr)
{
stack1.push(cur1);
cur1 = cur1->next;
}
while(cur2 != nullptr)
{
stack2.push(cur2);
cur2 = cur2->next;
}
ListNode* p = nullptr; //指向第一个相交的节点
while(!stack1.empty() && !stack2.empty() && stack1.top() == stack2.top())
{
p = stack1.top(); // 或者 p = stack2.top();
stack1.pop();
stack2.pop();
}
return p;
}
};
二、参照代码随想录的实现方法
代码随想录里给出的思路是将两个链表“右对齐”,然后两个指针分别从较短的链表头节点处开始遍历,如下图所示:
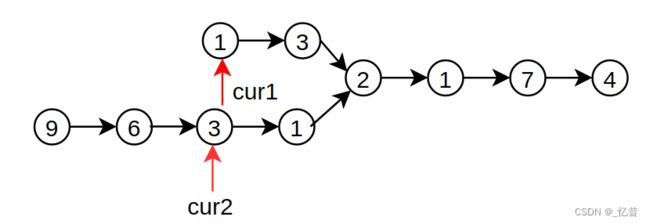
清楚了这个思路之后,代码实现就简单了,代码实现如下:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
if(headA == nullptr || headB == nullptr) return nullptr;
int size_A = 0,size_B = 0;
//遍历链表A,得到其长度
ListNode* cur_A = headA;
while(cur_A != nullptr)
{
cur_A = cur_A->next;
size_A++;
}
//遍历链表B,得到其长度
ListNode* cur_B = headB;
while(cur_B != nullptr)
{
cur_B = cur_B->next;
size_B++;
}
//计算长度差
int delta = abs(size_A - size_B);
//对齐
cur_A = headA;
cur_B = headB;
if(size_A > size_B)
while(delta--) cur_A = cur_A->next;
else
while(delta--) cur_B = cur_B->next;
//找交点
ListNode* p = nullptr;
while(cur_A != cur_B)
{
cur_A = cur_A->next;
cur_B = cur_B->next;
}
if(cur_A == cur_B) p = cur_A;
return p;
}
};
代码随想录的代码就不在这里给出了,具体可点击这里查看。
小结
这个题不难,自己想到的方法也可以实现,但是空间复杂度是O(n),时间复杂度还可以。代码随想录给出的方法代码看着繁琐,但是清楚思路之后就很简单了,空间复杂度为O(1)。
题目四:LeetCode 142.环形链表II
一、按照自己的想法实现
这个题之前做过,还有一些想象,难点在于数学推动,代码随想录给出的推倒不是很理解,这里按照自己的想法推倒一下。
首先判断是否有环,用两个指针fast和slow,两个指针都从头节点开始往后移动,fast指针每次移动两个节点,slow指针每次移动1个节点(理论上只要两个指针的移动速度不一样就可以了),这样如果有环的话这两个指针一定会在环内相遇,所以有环无环的判断还是挺简单的,难点在于入环节点,推倒如下:
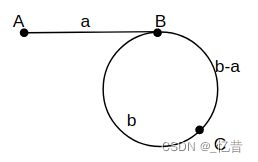
假设A为头节点,AB = a , 环的长度为b,设fast指针的移动速度v1 = 2,slow指针的移动速度v2 = 1。当slow指针到达B点时移动了距离a,此时fast指针移动了2a,减去AB段的距离,fast指针在环内移动了距离a,两个和指针在环内相遇u时满足下面的公式:
(a+2t) - t = mb , m = 1,2,3,..
其中m表示fast指针和slow指针第几次重合。(这个问题就是高中物理里的追击相遇问题)
取 m = 1,化简上面的公式:
t = b - a
上面的时间两个指针第一次重合的时间(从slow指针在B点开始移动时开始计时),因此可以得到两个指针第一次重合的位置距离B点顺时针b-a位置处(图中的C点),这样从C点顺时针到B点的距离为a,这个距离和A点到B点的距离相等,这样值只要让两个指针分别从A点和C点出发,每次移动一个节点,两个指针相遇的位置就是环的入口节点。推倒出这个结论之后代码实现就很简单了。代码如下:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
if(head == nullptr || head->next == nullptr) return nullptr;
ListNode* slow = head->next;
ListNode* fast = head->next->next;
while(fast != nullptr && fast->next != nullptr && slow != fast)
{
slow = slow->next; //每次移动一个节点
fast = fast->next->next; //每次移动两个节点
}
if(fast == nullptr || fast->next == nullptr) return nullptr;
//找环的入口
slow = head;
while(slow != fast)
{
slow = slow->next; //每次移动一个节点
fast = fast->next; //每次移动一个节点
}
return slow;
}
};
在写的时候遇到一些问题,这里记录一下:
- 初始化
ListNode* slow = head->next;
ListNode* fast = head->next->next;
初始化的时候两个指针就要移动了,不能都指向head,否则在第一个while循环处就直接跳过了。
- 第一个while循环条件
因为fast指针每次移动两个节点,所以需要同时判断fast和fast->next是否等于nullptr,且顺序不能颠倒。 - if(fast == nullptr || fast->next == nullptr) return nullptr
这里也需要对fast和fast->next进行判断缺一不可。
二、参考代码随想录的实现方法
上面的方法其实就是因为之前看过代码随想录的方法,在求解思路上一致,在数学推倒上不太明白代码随想录的推倒,所以自己推倒了一下,最终的结论是一样的。代码随想录给出的代码如下:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode* fast = head;
ListNode* slow = head;
while(fast != NULL && fast->next != NULL) {
slow = slow->next;
fast = fast->next->next;
// 快慢指针相遇,此时从head 和 相遇点,同时查找直至相遇
if (slow == fast) {
ListNode* index1 = fast;
ListNode* index2 = head;
while (index1 != index2) {
index1 = index1->next;
index2 = index2->next;
}
return index2; // 返回环的入口
}
}
return NULL;
}
};
小结
本题的代码实现不难,难点在于数学推倒,即怎么判断环的入口,只要能推倒出结论,代码实现就很简单了。
今日小结
今天有四个题,相对来说都不是很难。对链表的操作有时候涉及到很多指针,画图可以帮助理解链表的变化过程,有时候甚至需要先画图来确定处理过程,然后再转化为代码,两两交换那题就是如此,所以说在对链表的操作过程中画图是非常重要的。今天的题到此结束,明天终于可以休息一天了。照 这样的进度到后面不熟悉的部分肯定要跟不上了。