python实现k-means聚类算法(python实现)
k-means聚类算法是最经典的聚类算法,本文数据采用500二维条数据集
分为四个类
计算欧式距离模块在这里插入代码片
def getDistance(v1,v2):
# dis = np.sqrt(np.sum(np.square(v1 - v2))) #计算两个数据之间的欧式距离
dis = sqrt(sum(power(v1 - v2,2))) #v1,v2是两个数据点的坐标 (x1-x2)的平方+(y1-y2)的平方开根号得到距离
# dis = sqrt(power(v1 - v2, 2))
return dis
处理数据文件模块
def getDistance(v1,v2):
# dis = np.sqrt(np.sum(np.square(v1 - v2))) #计算两个数据之间的欧式距离
dis = sqrt(sum(power(v1 - v2,2))) #v1,v2是两个数据点的坐标 (x1-x2)的平方+(y1-y2)的平方开根号得到距离
# dis = sqrt(power(v1 - v2, 2))
return dis
初始化质心模块
def innitCentroid(dataSet,k):
return random.sample(dataSet,k) #初始化质心
计算每个类别的质心模块
def getCentroid(cenList,cenDiction): #计算每个类别中的质心
newcen = list()
for i in range(len(cenList)):
newcen.append(mean(array(cenDiction[i]),0).tolist()) #对于每个类别 计算所有坐标的平均值
print('新的质心',newcen)
return newcen
计算聚类模块
def minDistance(dataSet,cenList): #计算最小聚类,获得新的分类
cenDiction = {}
for item in dataSet:
mind = float("inf") #最大数 表示无穷大数
flag = 0
aitem = array(item) #list类型不能对数据进行运算 所以转换为array类型
for i in range(len(cenList)): #对于每个质心 计算每个数据点到质心的距离
acen = array(cenList[i])
if getDistance(aitem,acen) < mind:
mind = getDistance(aitem,acen)
# print(mind)
flag = i
if flag not in cenDiction.keys(): #如果质心不再分类字典的keys()中 加入
cenDiction[flag] = []
cenDiction[flag].append(item)
# print(cenDiction)
return cenDiction
计算方差模块
def getDeviation(cenList,cenDiction): #计算均方差
sum = 0
for i in range(len(cenList)):
item = cenList[i]
aitem = array(item)
for data in cenDiction[i]:
adata = array(data)
sum = sum + getDistance(aitem,adata)
return sum
显示图片模块
def showplot(cenList,cenDiction,newnum,oldnum):
colormark = ['or','og','ob','ok','oy','ow'] #o表示圆 d表示菱形
cenmark = ['dr','dg','db','dk','dy','dw']
plt.figure('k-means聚类')
for i in range(len(cenList)):
plt.plot(cenList[i][0],cenList[i][1],cenmark[i])
for item in cenDiction[i]:
plt.plot(item[0],item[1],colormark[i])
if abs(newnum - oldnum) < 0.0001:
plt.savefig("k-means.png")
plt.show()
第一次迭代
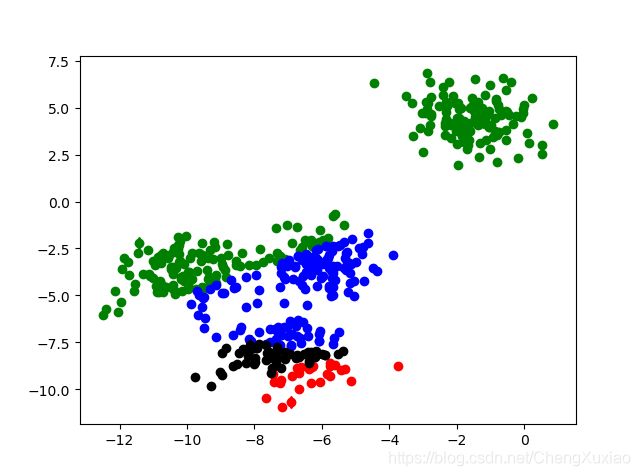
新的质心 [[-6.3204742186881715, -9.315093760527636], [-5.686493501230958, 0.34266093128677], [-6.632153415413944, -4.653307380704366], [-7.431619373196795, -8.30175325544197]]
第二次迭代效果图
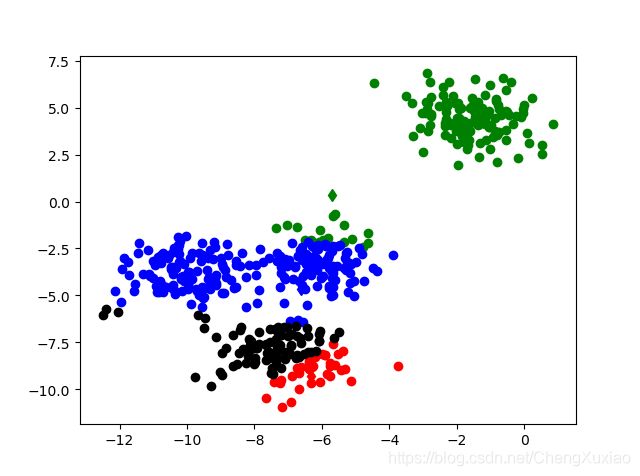
新的质心 [[-6.1893099419358695, -9.006325255392968], [-2.08113110707828, 3.6587271216146133], [-8.17711209582964, -3.6407743206173073], [-7.696088659673251, -7.691135694294057]]
…
不断的迭代下去
得到最后结果
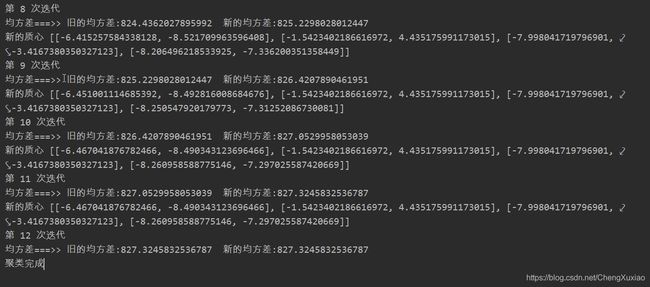
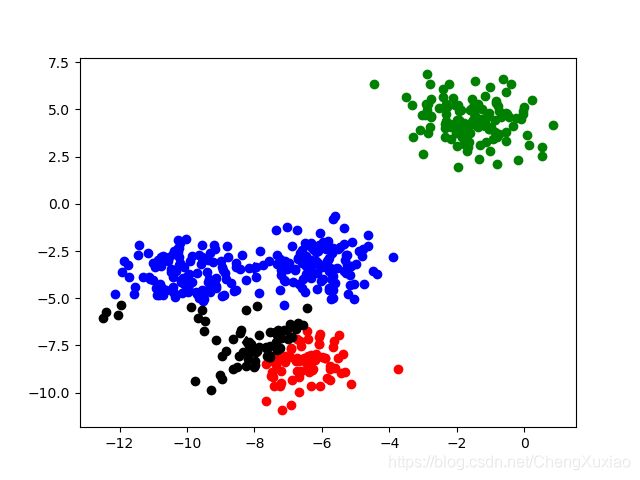
从上图的结果看出,划分为三个类比较好,效果如下:
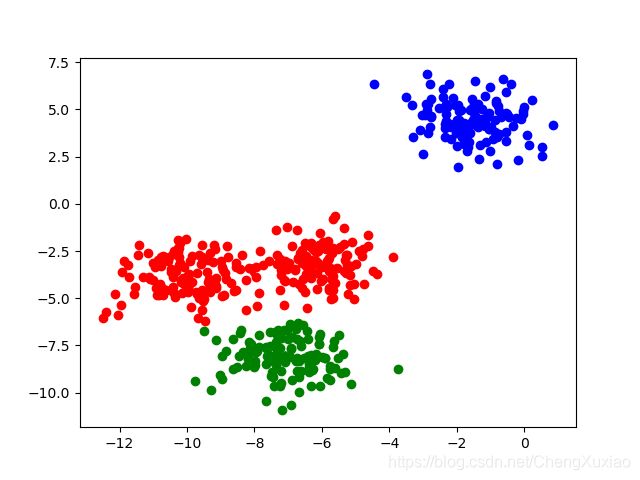
需要源码和数据的朋友,下载链接如下:
源码和数据下载链接