学习笔记(6)——感知机分类与序列标注
- 一、分类问题
-
- 1 定义
- 2 应用
- 二、线性分类模型
- 三、感知机算法
- 四、基于感知机的人名性别分类
- 五、结构化预测问题
-
- 1 定义
- 2 结构化预测与学习流程
- 六、线性模型的结构化感知机算法
-
- 1 结构化感知机算法
- 2 与感知机算法比较
- 3 结构化感知机与序列标注
- 七、基于结构化感知机的中文分词
隐马弥可夫模型能捕捉的特征仅限于两种: (1)前一个标签是什么;(2)当前字符是什么。
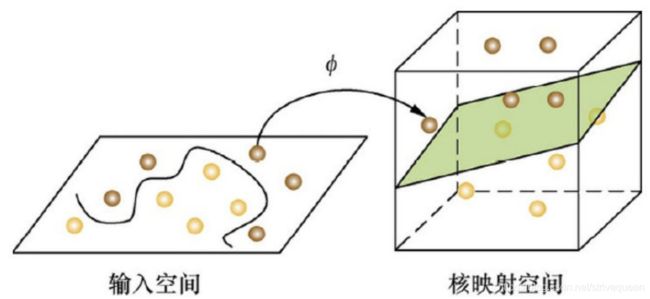
为了利用更多的特征,线性模型( linear model ) 应运而生。线性模型由两部分构成: 一系列用来提取特征的特征函数 φ,以及相应的权重向量 w。
本文将深入讲解感知机算法的原理,以及在分类和序列标注上的应用。在序列标注应用部分,我们将实现基于感知机的中文分词器。由于感知机序列标注基于分类,并且分类问题更简单,所以我们先学习分类问题。
一、分类问题
1 定义
分类指的是预测样本所属类别的一类问题。二分类也可以解决任意类别数的多分类问题(one vs rest)。
- 将类型class1看作正样本,其他类型全部看作负样本,然后就可以得到样本标记类型为该类型的概率 p1。
- 然后再将另外类型class2看作正样本,其他类型全部看作负样本,同理得到 p2。
- 以此循环,可以得到该待预测样本的标记类型分别为类型 class i 时的概率 pi,最后取 pi 中最大的那个概率对应的样本标记类型作为我们的待预测样本类型。
- 总之还是以二分类来依次划分,并求出最大概率结果。
2 应用
在NLP领域,绝大多数任务可以用分类来解决。文本分类天然就是一个分类问题。关键词提取时,对文章中的每个单词判断是否属于关键词,于是转化为二分类问题。在指代消解问题中,对每个代词和每个实体判断是否存在指代关系,又是一个二分类问题。在语言模型中,将词表中每个单词作为一种类别,给定上文预测接下来要出现的单词。
二、线性分类模型
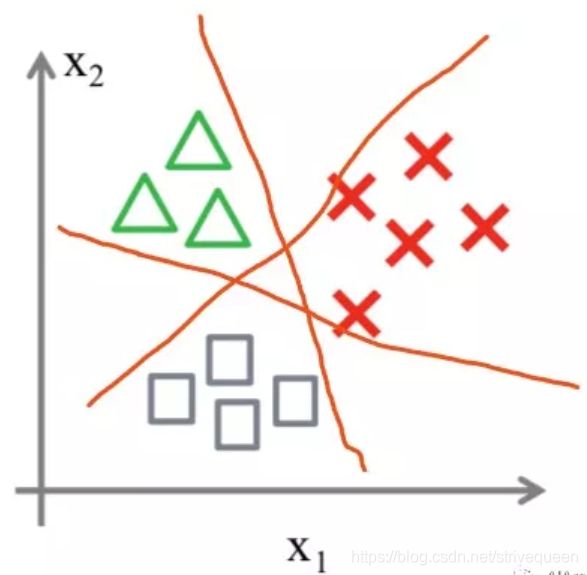
线性模型是传统机器学习方法中最简单最常用的分类模型,用一条线性的直线或高维平面将数据一分为二。

直线将平面分割为两部分,分别对应男女。对于任何姓名,计算它落入哪个区域,就能预测它的性别。这样的区域称为决策区域,它们的边界称为决策边界。二维空间中,如果决策边界是直线,则称为线性分类模型: Y = Wx + b。
推广到 D 维空间,分离超平面的方程为:
∑ i = 1 D w i x i + b = 0 \sum_{i=1}^{D} w_{i} x_{i}+b=0 i=1∑Dwixi+b=0
其中,w 是权重,b 偏置(截距),可以写成向量的形式:
w = [ w 1 , ⋯ , w D , b ] x = [ x 1 , ⋯ , x D , 1 ] y ^ = sign ( w ⋅ x ) = { − 1 , w ⋅ x ⩽ 0 1 , w ⋅ x > 0 \begin{array}{l} \boldsymbol{w}=\left[w_{1}, \cdots, w_{D}, b\right] \\ x=\left[x_{1}, \cdots, x_{D}, 1\right] \\ \hat{y}=\operatorname{sign}(\boldsymbol{w} \cdot \boldsymbol{x})=\left\{\begin{array}{cl} -1, & \boldsymbol{w} \cdot \boldsymbol{x} \leqslant 0 \\ 1, & \boldsymbol{w} \cdot \mathbf{x}>0 \end{array}\right. \end{array} w=[w1,⋯,wD,b]x=[x1,⋯,xD,1]y^=sign(w⋅x)={−1,1,w⋅x⩽0w⋅x>0
三、感知机算法
找出这个分离超平面其实就是感知机算法。感知机算法则是一种迭代式的算法:在训练集上运行多个迭代,每次读入一个样本,执行预测,将预测结果与正确答案进行对比,计算误差,根据误差更新模型参数,再次进行训练,直到误差最小为止。
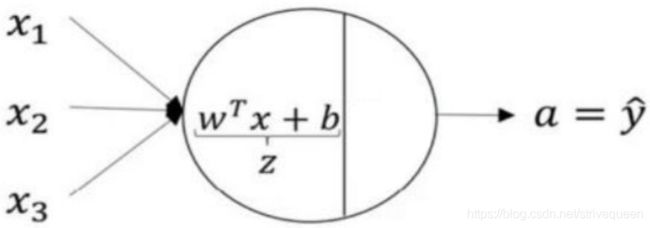
- 损失函数: 从数值优化的角度来讲,迭代式机器学习算法都在优化(减小)一个损失函数( loss function )。损失函数 J(w) 用来衡量模型在训练集上的错误程度,自变量是模型参数 w,因变量是一个标量,表示模型在训练集上的损失的大小。
- 梯度下降: 给定样本,其特征向量 x 只是常数,对 J(w) 求导,得到一个梯度向量 Δw,它的反方向一定是当前位置损失函数减小速度最快的方向。如果参数点 w 反方向移动就会使损失函数减小,叫梯度下降。
- 学习率: 梯度下降的步长叫做学习率。
- 随机梯度下降(SGD): 如果算法每次迭代随机选取部分样本计算损失函数的梯度,则称为随机梯度下降。

假如数据本身线性不可分,感知机损失函数不会收敛,每次迭代分离超平面都会剧烈振荡。这时可以对感知机算法打补丁,使用投票感知机或平均感知机。
投票感知机和平均感知机
投票感知机:每次迭代的模型都保留,准确率也保留,预测时,每个模型都给出自己的结果,乘以它的准确率加权平均值作为最终结果。
投票感知机要求存储多个模型及加权,计算开销较大,更实际的做法是取多个模型的权重的平均,这就是平均感知机。
四、基于感知机的人名性别分类
解决人名性别分类的监督学习流程:
- 标注人名分类语料库
- 利用感知机算法训练线性模型
- 利用线性模型给人名分类,评估准确率。
- 人名性别语料库
1.人名性别语料库
人名性别语料库:cnname。运行下面代码后会自动下载。语料格式为逗号分隔的 .csv,第一列为姓名,第二列为性别:
赵伏琴,女
钱沐杨,男
孙竹珍,女
李潮阳,男
2. 训练
代码详见:classify_name.py
https://github.com/NLP-LOVE/Introduction-NLP/tree/master/code/ch05/classify_name.py
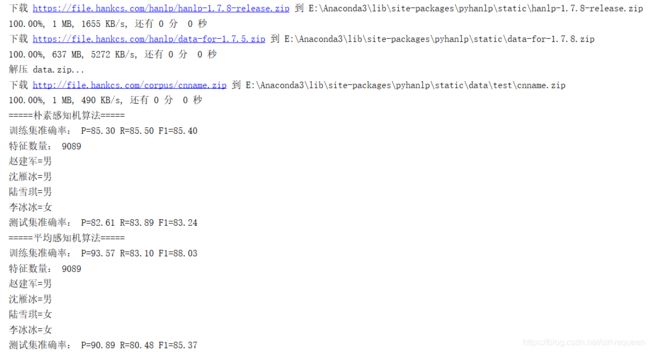
运行结果如下:
五、结构化预测问题
自然语言处理问题大致可分为两类,一种是分类问题,另一种就是结构化预测问题,序列标注只是结构化预测的一个特例,对感知机稍作拓展,分类器就能支持结构化预测。
1 定义
信息的层次结构特点称作结构化。那么结构化预测(structure prediction) 则是预测对象结构的一类监督学习问题。相应的模型训练过程称作结构化学习(structured learning )。分类问题的预测结果是一个决策边界, 回归问题的预测结果是一个实数标量,而结构化预测的结果则是一个完整的结构。
自然语言处理中有许多任务是结构化预测,比如序列标注预测结构是一整个序列,句法分析预测结构是一棵句法树,机器翻译预测结构是一段完整的译文。这些结构由许多部分构成,最小的部分虽然也是分类问题(比如中文分词时每个字符分类为{B,M,E,S} ),但必须考虑结构整体的合理程度。
2 结构化预测与学习流程
结构化预测的过程就是给定一个模型 λ 及打分函数 score,利用打分函数给一些备选结构打分,选择分数最高的结构作为预测输出,公式如下:
y ^ = arg max y ∈ Y score λ ( x , y ) \hat{y}=\arg \max _{y \in Y} \operatorname{score}_{\lambda}(x, y) y^=argy∈Ymaxscoreλ(x,y)
其中,Y 是备选结构的集合。既然结构化预测就是搜索得分最高的结构 y,那么结构化学习的目标就是想方设法让正确答案 y 的得分最高。不同的模型有不同的算法,对于线性模型,训练算法为结构化感知机。
六、线性模型的结构化感知机算法
1 结构化感知机算法
要让线性模型支持结构化预测,必须先设计打分函数。打分函数的输入有两个缺一不可的参数: 特征 x 和结构 y。但之前介绍的线性模型的“打分函数”只接受一个自变量 x。
做法是定义新的特征函数 ϕ(x,y),把结构 y 也作为一种特征,输出新的“结构化特征向量”。新特征向量与权重向量做点积后,就得到一个标量,将其作为分数:
score ( x , y ) = w ⋅ ϕ ( x , y ) \operatorname{score}(x, y)=w \cdot \phi(x, y) score(x,y)=w⋅ϕ(x,y)
打分函数有了,取分值最大的结构作为预测结果,得到结构化预测函数:
y ^ = arg max y ∈ Y ( w ⋅ ϕ ( x , y ) ) \hat{y}=\arg \max _{y \in Y}(w \cdot \phi(x, y)) y^=argy∈Ymax(w⋅ϕ(x,y))
预测函数与线性分类器的决策函数很像,都是权重向量点积特征向量。那么感知机算法也可以拓展复用,得到线性模型的结构化学习算法。
- 读入样本 (x,y),进行结构化预测: y ^ = arg max y ∈ Y ( w ⋅ ϕ ( x , y ) ) \hat{y}=\arg \max _{y \in Y}(w \cdot \phi(x, y)) y^=argmaxy∈Y(w⋅ϕ(x,y))
- 与正确答案相比,若不相等,则更新参数: 奖励正确答案触发的特征函数的权重,否则进行惩罚: w ← w + ϕ ( x ( i ) , y ) − ϕ ( x ( i ) , y ^ ) w \leftarrow w+\phi\left(x^{(i)}, y\right)-\phi\left(x^{(i)}, \hat{y}\right) w←w+ϕ(x(i),y)−ϕ(x(i),y^)
- 还可以调整学习率: w ← w + α ( ϕ ( x ( i ) , y ) − ϕ ( x ( i ) , y ^ ) ) \boldsymbol{w} \leftarrow \boldsymbol{w}+\alpha\left(\phi\left(\boldsymbol{x}^{(i)}, \boldsymbol{y}\right)-\phi\left(\boldsymbol{x}^{(i)}, \hat{\boldsymbol{y}}\right)\right) w←w+α(ϕ(x(i),y)−ϕ(x(i),y^))
2 与感知机算法比较
- 结构化感知机修改了特征向量。
- 结构化感知机的参数更新赏罚分明。
3 结构化感知机与序列标注
上面已经讲了结构化感知机的模型公式,看如何运用到序列标注上,我们知道序列标注最大的结构特点就是标签相互之间的依赖性,对于结构化感知机,就可以使用转移特征来表示:
ϕ k ( y t − 1 , y t ) = { 1 , y t − 1 = s i , H y t = s j i = 0 , ⋯ , N ; j = 1 , ⋯ , N 0 , \phi_{k}\left(y_{t-1}, y_{t}\right)=\left\{\begin{array}{l} 1, \quad y_{t-1}=s_{i}, \mathrm{H} y_{t}=s_{j} \quad i=0, \cdots, N ; j=1, \cdots, N \\ 0, \end{array}\right. ϕk(yt−1,yt)={1,yt−1=si,Hyt=sji=0,⋯,N;j=1,⋯,N0,
其中,Yt 为序列第 t 个标签,Si 为标注集第 i 种标签,N 为标注集大小。
状态特征如下,类似于隐马尔可夫模型的发射概率矩阵,状态特征只与当前的状态有关,与之前的状态无关:
ϕ i ( x i , y i ) = { 1 0 \phi_{i}\left(x_{i}, y_{i}\right)=\left\{\begin{array}{l} 1 \\ 0 \end{array}\right. ϕi(xi,yi)={10
于是,结构化感知机的特征函数就是转移特征和状态特征的合集:
ϕ = [ ϕ k ; ϕ l ] k = 1 , ⋯ , N 2 + N ; l = N 2 + N + 1 , ⋯ \phi=\left[\phi_{k} ; \phi_{l}\right] \quad k=1, \cdots, N^{2}+N ; l=N^{2}+N+1, \cdots ϕ=[ϕk;ϕl]k=1,⋯,N2+N;l=N2+N+1,⋯
基于以上公式,我们统一用打分函数来表示:
score ( x , y ) = ∑ t = 1 T w ⋅ ϕ ( y t − 1 , y t , x t ) \operatorname{score}(\boldsymbol{x}, \boldsymbol{y})=\sum_{t=1}^{T} \boldsymbol{w} \cdot \phi\left(y_{t-1}, y_{t}, \boldsymbol{x}_{t}\right) score(x,y)=t=1∑Tw⋅ϕ(yt−1,yt,xt)
有了打分公式,就可以利用维特比算法求解得分最高的序列。
七、基于结构化感知机的中文分词
代码详见: perceptron_cws.py
https://github.com/NLP-LOVE/Introduction-NLP/tree/master/code/ch05/perceptron_cws.py
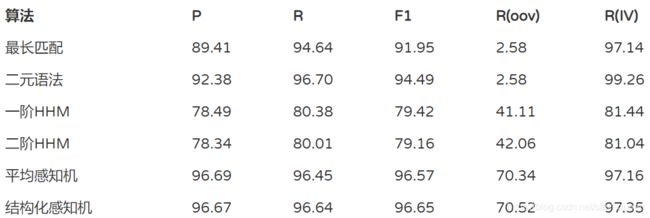
对比各项指标,我们终于将 OOV 提高到了 70% 以上,并且综合 F1 也提高了 96.7%,感知机是截止到这章最好用的算法,完全达到了实用水平,在实际项目中,无非还需要挂载一些领域词库。
参考文献
《自然语言处理入门》——5. 感知机分类与序列标注