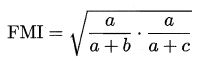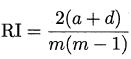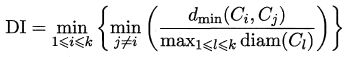《机器学习》周志华--第9章聚类 笔记+习题

https://www.cnblogs.com/hzcya1995/p/13302691.html

9.1聚类任务

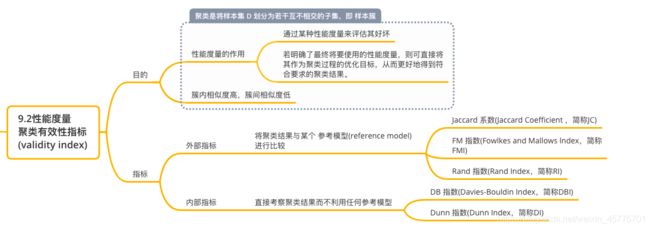
9.2性能度量

基于式 (9.1 ) ~ (9.4)，可导出下面这些常用的聚类性能度量外部指标：

• Jaccard 系数(Jaccard Coefficient ，简称JC)
  
• FM 指数(Fowlkes and Mallows lndex，简称FMI)

• Rand 指数(Rand Index，简称RI)
  
  

基于这四个式子，可导出下面这些常用的聚类性能度量内部指标：

• DB 指数(Davies-Bouldin Index，简称DBI)
• Dunn 指数(Dunn Index，简称DI)
  显然， DBI 的值越小越好，而 DI 则相反，值越大越好。

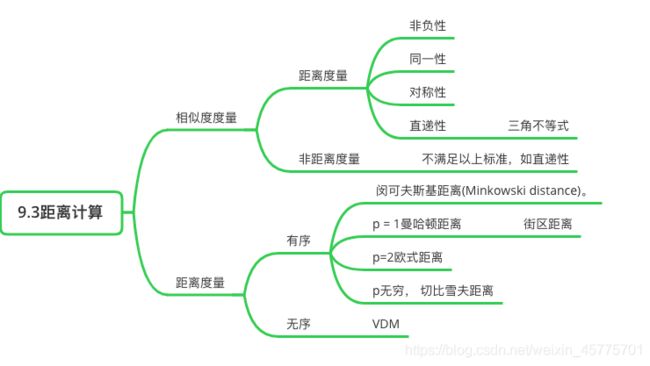
9.3距离计算

距离度量

有序距离

属性经常划分为 连续属性(continuous attribute)，亦称 数值属性(numerical att巾ute)；和 离散属性(categorical attribute)，亦称 列名属性(nominal attribute)。前者在定义域上有无穷多个可能的取值，后者在定义域上是有限个取值。

然而，在讨论距离计算时，属性上是否定了"序"关系更为重要。

无序距离

9.4原型聚类

• k 均值算法
  

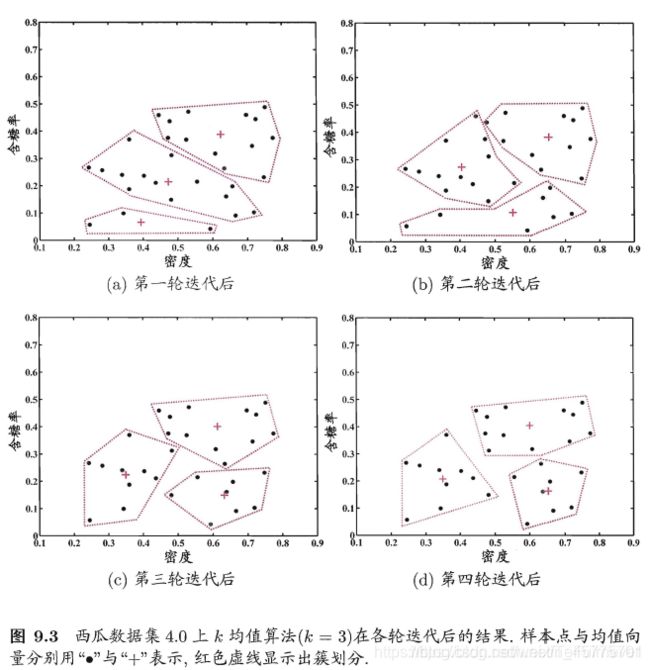
其中第 1 行对均值向量进行初始化，在第 4-8 行与第 9一16 行依次对当前簇划分及均值向量选代更新，若迭代更新后聚类结果保持不变，则在第 18 行将当前簇划分结果返回。

• 学习向量量化
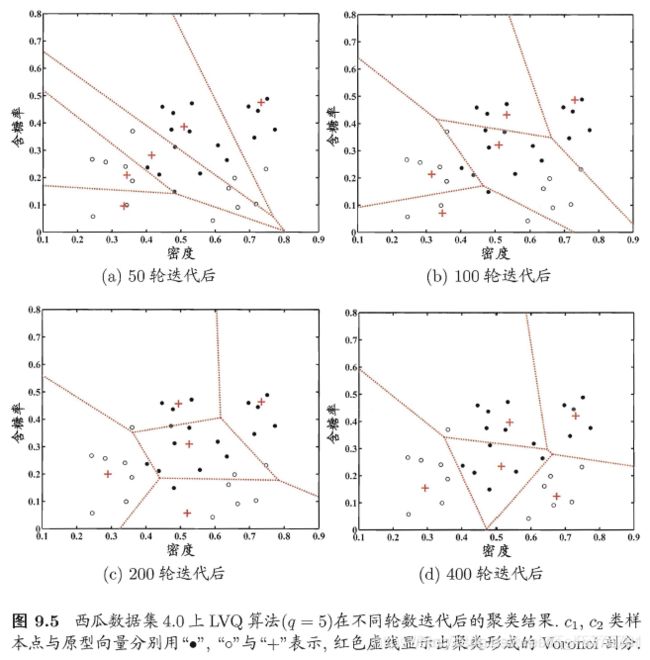
  与 k 均值算法类似，学习向量量化(Learning Vector Quantization，简称LVQ) 也是试图找到一组原型向量来刻画聚类结构， 但与一般聚类算法不同的是， LVQ 假设数据样本带有类别标记，学习过程利用样本的这些监督信息来辅助聚类。
  
  LVQ 算法描述如下图所示：
  
  
  
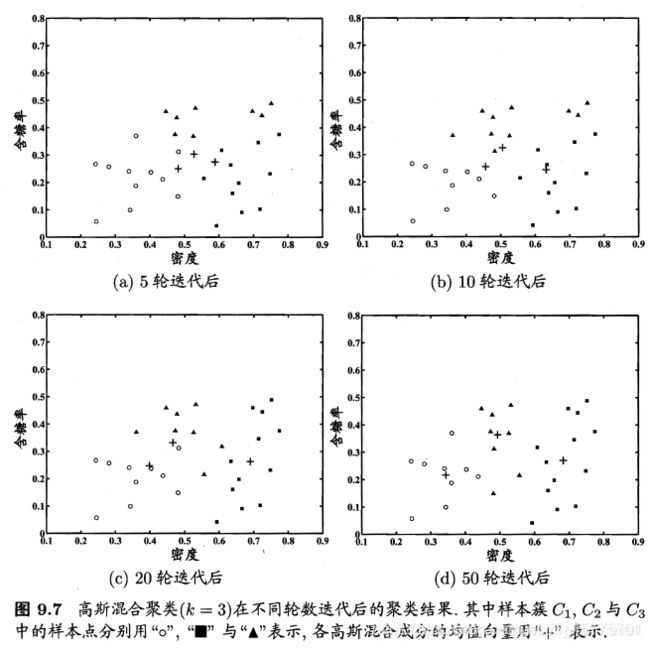
• 高斯混合聚类

高斯混合聚类与 k 均值、LVQ 用原型向量来刻画聚类结构不同，高斯混合(Mixture-of-Gaussian)聚类 采用概率模型来表达聚类原型。

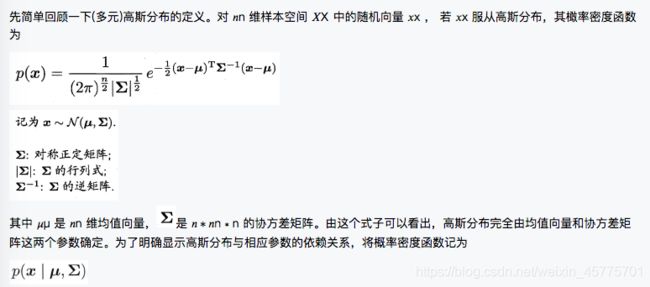
因此，从原型聚类的角度来看，高斯混合聚类是采用概率模型(高斯分布)对原型进行刻画，簇划分则由原型对应后验概率确定。那么模型参数如何求解呢?

可采用极大似然估计，即最大化(对数)似然：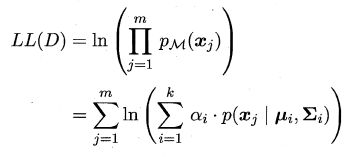
常采用EM 算法进行迭代优化求解。

若参数能最大化似然函数，则由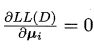
有如下


即每个高斯成分的混合系数由样本属于该成分的平均后验概率确定。

由上述推导即可获得高斯混合模型的 EM 算法。

高斯混合聚类算法描述如下图所示：

9.5密度聚类

简单来说，就是字面意思，核心对象的核心，密度直达的直达，密度可达的可达，密度相连的相连，就好比集合之间的碰撞一下。

基于这些概念， DBSCAN 将"簇"定义为：由密度可达关系导出的最大的密度相连样本集合。形式化地说，给定邻域参数 ， 簇 C 是满足以下性质的非空样本子集：
于是， DBSCAN 算法先任选数据集中的一个核心对象为种子(seed)，再由此出发确定相应的聚类簇，算法描述如下所示：
在第 1-7 行中，算法先根据给定的邻域参数找出所有核心对象；然后在第 10-24 行中，以任一核心对象为出发点，找出由其密度可达的样本生成聚类簇，直到所有核心对象均被访问过为止。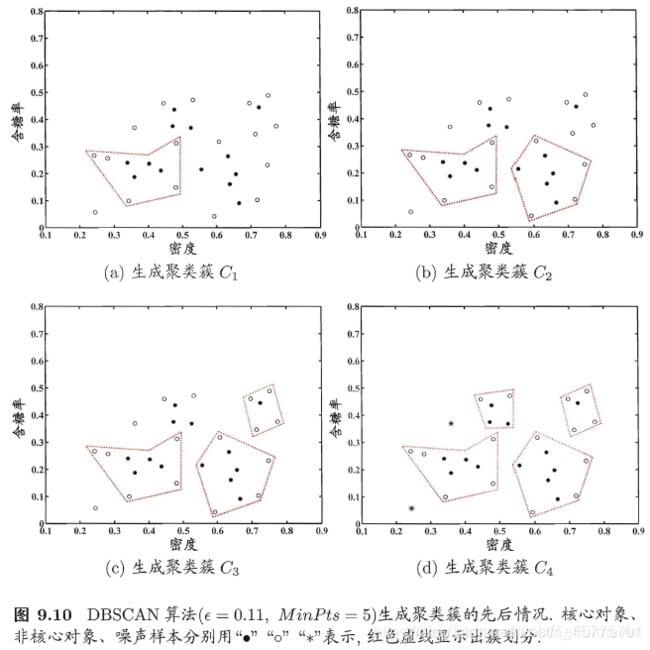

9.6层次聚类

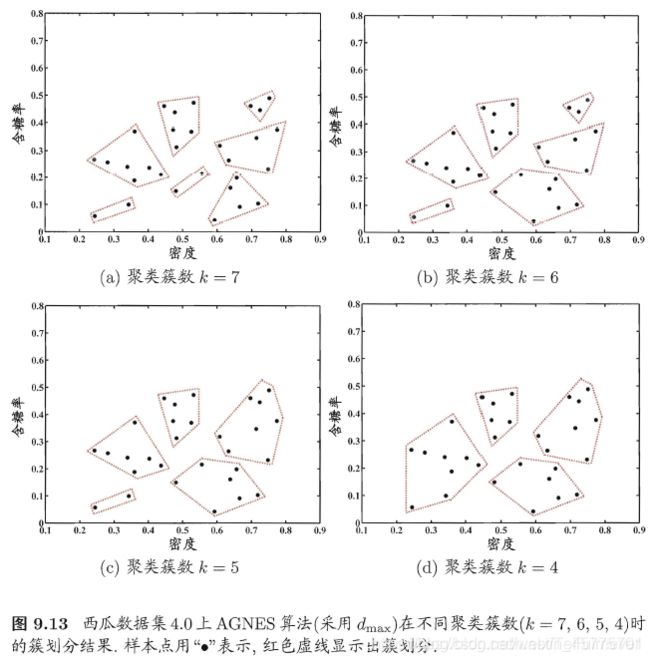
在第 1-9 行，算法先对仅含一个样本的初始聚类簇和相应的距离矩阵进行初始化；然后在第 11-23 行， AGNES 不断合
并距离最近的聚类簇，井对合并得到的聚类簇的距离矩阵进行更新;上述过程不断重复，直至达到预设的聚类簇数。

补充
聚类也许是机器学习中"新算法"出现最多、最快的领域一个重要原因是聚类不存在客观标准;给定数据集7 总能从某个角度找到以往算法未覆盖的某种标准从而设计出新算法。相对于机器学习其他分支来说， 聚类的知识还不够系统化。因此著名教科书 [Mitchell，1997] 中甚至没有关于聚类的章节，但聚类技术本身在现实任务中非常重要！！！

聚类性能度量除上面的内容外，常见的还有：

• F 值 互信息(mutual information) 平均廓宽(average silhouette width)等等

距离计算是很多学习任务的核心技术。间可夫斯基距离提供了距离计算的一般形式，除闵可夫斯基距离之外，内积距离、余弦距离等也很常用。

习题

https://www.cnblogs.com/hzcya1995/p/13302681.html

回顾一下性质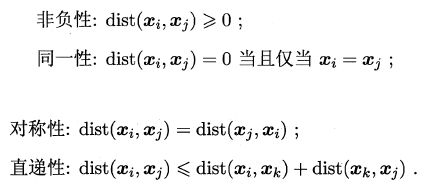
非负性、同一性、对称性很显然都是符合的，关键是直递性了，关于直递性就是闵可夫斯基不等式的证明，具体参考：闵可夫斯基不等式link.

不能，因为 k 均值本身是 NP 问题，而且 9.24 是非凸的（具体证明不太懂），容易陷入局部最优，所以在使用 k 均值时常常多次随机初始化中心点，然后在中心点附近挑选结果最好的一个，即局部最优解，无法找到全局最优解。

代码如下

import numpy as np
import matplotlib.pyplot as plt
from scipy.spatial import ConvexHull


class KMeans(object):
    def __init__(self, k):
        self.k = k

    def fit(self, X, initial_centroid_index=None, max_iters=10, seed=16, plt_process=False):
        m, n = X.shape
        # 没有指定中心点时，随机初始化中心点
        if initial_centroid_index is None:
            np.random.seed(seed)
            initial_centroid_index = np.random.randint(0, m, self.k)
        centroid = X[initial_centroid_index, :]
        idx = None

        # 打开交互模式
        plt.ion()
        for i in range(max_iters):
            # 按照中心点给样本分类
            idx = self.find_closest_centroids(X, centroid)
            if plt_process:
                self.plot_converge(X, idx, initial_centroid_index)
            # 重新计算中心点
            centroid = self.compute_centroids(X, idx)
        # 关闭交互模式
        plt.ioff()
        plt.show()
        return centroid, idx

    def find_closest_centroids(self, X, centroid):
        # 这种方式利用 numpy 的广播机制，直接计算样本到各中心的距离，不用循环，速度比较快，但是在样本比较大时，更消耗内存
        distance = np.sum((X[:, np.newaxis, :] - centroid) ** 2, axis=2)
        idx = distance.argmin(axis=1)
        return idx

    def compute_centroids(self, X, idx):
        centroids = np.zeros((self.k, X.shape[1]))
        for i in range(self.k):
            centroids[i, :] = np.mean(X[idx == i], axis=0)
        return centroids

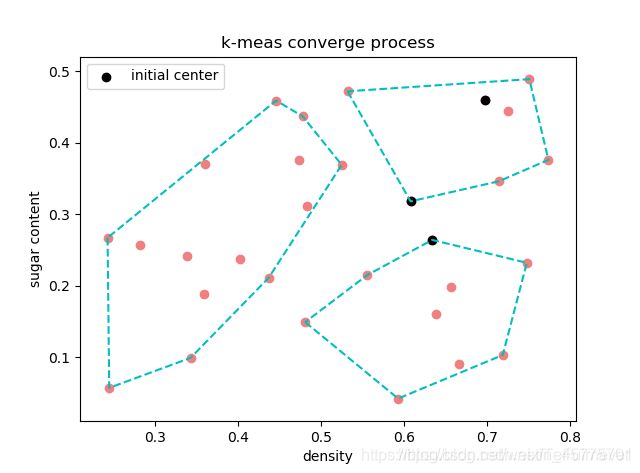
    def plot_converge(self, X, idx, initial_idx):
        plt.cla() # 清除原有图像
        plt.title("k-meas converge process")
        plt.xlabel('density')
        plt.ylabel('sugar content')
        plt.scatter(X[:, 0], X[:, 1], c='lightcoral')
        # 标记初始化中心点
        plt.scatter(X[initial_idx, 0], X[initial_idx, 1], label='initial center', c='k')
        # 画出每个簇的凸包
        for i in range(self.k):
            X_i = X[idx == i]
            # 获取当前簇的凸包索引
            hull = ConvexHull(X_i).vertices.tolist()
            hull.append(hull[0])
            plt.plot(X_i[hull, 0], X_i[hull, 1], 'c--')
        plt.legend()
        plt.pause(0.5)


if __name__ == '__main__':
    data = np.loadtxt('..\data\watermelon4_0_Ch.txt', delimiter=', ')
    centroid, idx = KMeans(3).fit(data, plt_process=True, seed=24)

最小距离由两个簇的最近样本决定，最大距离由两个簇的最远样本决定。具体区别如下：

• 最大距离，可以认为是所有类别首先生成一个能包围所有类内样本的最小圆，然后所有圆同时慢慢扩大相同的半径，直到某个类圆能完全包围另一个类的所有点就停止，并合并这两个类。由于此时的圆已经包含另一个类的全部样本，所以称为全连接。

• 最小距离，可以认为是扩大时遇到第一个非自己类的点就停止，并合并这两个类。由于此时的圆只包含另一个类的一个点，所以称为单连接。

• 原型聚类：输出线性分类边界的聚类算法显然都是凸聚类，这样的算法有：K均值，LVQ；而曲线分类边界的也显然是非凸聚类，高斯混合聚类，在簇间方差不同时，其决策边界为弧线，所以高混合聚类为非凸聚类；

• 密度聚类：DBSCAN是非凸聚类；

• 层次聚类：AGENS是凸聚类。
  
  暂无待补