阳云yy

K近邻（KNN）原理及python实现

文章目录

一、KNN算法原理
二、KNN算法三要素
三、K值的选择
- - - K值的选择方法
    - 交叉验证选取 $k$ 值
四、距离度量的方式
五、分类决策规则
六、KNN算法的优点和缺点
七、python程序实现
- 7.1 电影类别分类
- 7.2 KNN入门学习代码
- 7.3 sklearn实现KNN算法

一、KNN算法原理

K最近邻（K-Nearest Neighbor,KNN）算法核心思想是一个样本与数据集中的 $k$ 个样本最相似，如果这 $k$ 个样本中的大多数属于某一个类别，则该样本也属于这个类别。也就是说，该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。KNN方法在类别决策时，只与极少量的相邻样本有关。 $k$ 通常是不大于20的整数。

我们以下图为例，当要判断绿色实例的类别的时候，我们可以看看它的附近有红色三角形和蓝色矩形，然后在第一个最近邻实线圈内采取多数表决的决策规则，发现绿球周围红色三角形多于蓝色矩形，于是把绿色实例也分类为红色那一类。

二、KNN算法三要素

k值的选取
距离度量的方式
分类决策规则

三、K值的选择

一般根据样本的分布，选择一个较小的值，通过交叉验证选择一个合适的 $k$ 值(通常小于20的整数)
$k$ 值较小，就相当于用较小的区域中的训练实例进行预测，训练误差会减小，只有与输入实例较近或相似的训练实例才会对预测结果起作用，与此同时带来的问题是泛化误差会增大。
$k$ 值较大，就相当于用较大区域中的训练实例进行预测，其优点是可以减少泛化误差，但缺点是训练误差会增大。此时与输入实例较远（不相似的）训练实例也会对预测器作用，使预测发生错误，且K值的增大就意味着整体的模型变得简单。
一个极端的情况是 $k$ = $m$ ，此时完全没有分类，此时无论输入实例是什么，都只是简单的预测它属于在训练实例中最多的类，模型过于简单。

K值的选择方法

从 $k$ 等于训练集中样本数量的平方根开始。比如训练集中有100个案例，则 $k$ 可以从10开始进行进行进一步筛选。
基于各种测试数据测试多个k值，并选择一个可以提供最好分类性能的 $k$ 值。除非数据的噪声非常大，否则大的训练集可以使 $k$ 值的选择不那么重要。
选择一个较大的 $k$ 值，同时用一个权重投票，在这个过程中，认为较近邻的投票比远的投票权重更大。

交叉验证选取 $k$ 值

在许多实际应用中数据是不充足的。为了选择好的模型，可以采用交叉验证方法。交叉验证的基本想法是重复地使用数据，把给定的数据进行切分，将切分的数据组合为训练集与测试集，在此基础上反复进行训练测试以及模型的选择。在实现过程中将采用 sklearn.model_selection.cross_val_score() 实现交叉验证选取 $k$ 值。

四、距离度量的方式

距离度量方式有三种：欧式距离、曼哈顿距离、闵可夫斯基距离。
欧式距离:
$y)=\sqrt{\sum_{k=1}^{n}\left(x_{k}-y_{k}\right)^{2}}$
最常用的就是欧式距离。
曼哈顿距离：
$d(x,y)=\sum\limits_{k=1}^{n}{\left| {{x}_{k}}-{{y}_{k}} \right|}$
闵可夫斯基距离:
$y)=\sqrt{\sum_{k=1}^{n}\left(x_{k}-y_{k}\right)^{2}}D(x, y)=\sqrt[p]{\left(\left|x_{1}-y_{1}\right|\right)^{p}+\left(\left|x_{2}-y_{2}\right|\right)^{p}+\ldots+\left(\left|x_{n}-y_{n}\right|\right)^{p}}=\sqrt[p]{\sum_{i=1}^{n}\left(\left|x_{i}-y_{i}\right|\right)^{p}}$
我们可以发现，欧式距离是闵可夫斯基距离距离在 $p = 2$ 时的特例，而曼哈顿距离是 $p = 1$ 时的特例。

五、分类决策规则

分类决策规则一般使用多数表决法。即如果一个样本在特征空间中的 $k$ 个最相似（即特征空间中最邻近）的样本中的大多数属于某一个类别，则该样本也属于这个类别。
KNN算法的计算过程：
步骤一：输入训练集数据和标签，输入测试数据；
步骤二：计算测试数据与各个训练数据之间的距离；
步骤三：按照距离的递增关系进行排序，选取距离最小的 $K$ 个点；
步骤四：确定前K个点所在类别的出现频率，返回前 $K$ 个点中出现频率最高的类别作为测试数据的预测分类。

六、KNN算法的优点和缺点

KNN算法的优点:

KNN可以用来做分类也可以用来做回归；
可用于非线性分类；
训练时间复杂度比支持向量机之类的算法低，仅为 $O (n)$ ；
KNN与朴素贝叶斯之类的算法比，对数据没有假设，准确度高，对异常点不敏感；
KNN方法主要靠周围有限个邻近的样本，而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为适合；
KNN算法比较适用于样本容量比较大的类域的自动分类，而那些样本容量较小的类域采用这种算法比较容易产生误分；
特别适合于多分类问题（对象具有多个类别标签），KNN要比SVM表现要好。

KNN算法的缺点:

特征数比较多时，计算量很大；
样本各类别数量不平衡时，对稀有类别的预测准确率低；
KD树，球树的模型建立需要大量的内存空间；
预测时需要现算预测点到训练集中所有点的距离，因此预测速度比逻辑回归算法要慢。

七、python程序实现

7.1 电影类别分类

数据推测《唐人街探案》属于那种电影类型。

python代码如下：

import math
# 使用字典构建数据集
movie_data = {"宝贝当家": [45, 2, 9, "喜剧片"],
              "美人鱼": [21, 17, 5, "喜剧片"],
              "澳门风云3": [54, 9, 11, "喜剧片"],
              "功夫熊猫3": [39, 0, 31, "喜剧片"],
              "谍影重重": [5, 2, 57, "动作片"],
              "叶问3": [3, 2, 65, "动作片"],
              "伦敦陷落": [2, 3, 55, "动作片"],
              "我的特工爷爷": [6, 4, 21, "动作片"],
              "奔爱": [7, 46, 4, "爱情片"],
              "夜孔雀": [9, 39, 8, "爱情片"],
              "代理情人": [9, 38, 2, "爱情片"],
              "新步步惊心": [8, 34, 17, "爱情片"]}

# 测试样本  唐人街探案": [23, 3, 17, "？片"]
#下面为求与数据集中所有数据的距离代码：
x = [23, 3, 17]
KNN = []
# 计算唐人街探案到每个点的距离，此处使用的欧氏距离，保留两位小数
for key, v in movie_data.items():
    d = math.sqrt((x[0] - v[0]) ** 2 + (x[1] - v[1]) ** 2 + (x[2] - v[2]) ** 2)
    KNN.append([key, round(d, 2)])

# 输出所用电影到 唐人街探案的距离
print(KNN)

#按照距离大小进行递增排序
KNN.sort(key=lambda dis: dis[1])

#选取距离最小的k个样本，这里取k=5；
KNN=KNN[:5]
print(KNN)

#确定前k个样本所在类别出现的频率，并输出出现频率最高的类别
labels = {"喜剧片":0,"动作片":0,"爱情片":0}
for s in KNN:
    label = movie_data[s[0]]
    labels[label[3]] += 1
labels =sorted(labels.items(),key=lambda l: l[1],reverse=True)
print(labels,labels[0][0],sep='\n')

输出结果：

[('喜剧片', 4), ('动作片', 1), ('爱情片', 0)]

测试代码来源https://blog.csdn.net/saltriver/article/details/52502253

7.2 KNN入门学习代码

链接: https://www.bilibili.com/video/BV1Nt411i7oD?vd_source=46c7da561c57eb4be6a24d9f87da11b1

import csv
import random

# 读取数据
with open("Prostate_Cancer.csv", "r") as file:
    reader = csv.DictReader(file)  # 借用字典读取文件
    # for row in reader:
    #     print(row)
    datas = [row for row in reader]  # 将数据全部读出，放到列表中
    # print(datas)

# 分组：分成两组，一组学习，一组出结果
random.shuffle(datas)  # 打乱列表顺序，便于切割，不产生特殊结果
n = len(datas) // 3
test_set = datas[0: n]  # 测试集
train_set = datas[n:]  # 训练集

# KNN开始
# 计算距离
def distance(d1, d2):
    sums = 0
    for key in ("radius", "texture", "perimeter", "area", "smoothness", "compactness", "symmetry", "fractal_dimension"):
        sums += (float(d1[key]) - float(d2[key])) ** 2
    return sums ** 0.5
    
K = 5

def knn(data):
    # 1、距离
    res = [
        {"result": train["diagnosis_result"], "distance": distance(data, train)}  # 返回结果与调用distance方法来你计算data和train之间的距离
        for train in train_set  # 遍历训练集
    ]

    # print(res)

    # 2、排序--升序
    res = sorted(res, key=lambda item: item["distance"])
    # print(res)
    # 3、提取前K个
    res1 = res[0:K]
    # print(res1)
    # 4、加权平均
    result = {"B": 0, "M": 0}  # 最终的返回结果

    # 总距离
    sum = 0
    for r in res1:
        sum += r["distance"]

    for r in res1:
        result[r["result"]] += 1 - r["distance"]/sum

    if result["B"] > result["M"]:
        return"B"
    else :
        return"M"

# 测试阶段
correct = 0
for test in test_set:
    result = test["diagnosis_result"]
    result1 = knn(test)

    if result == result1:
        correct += 1

print("准确率为：{:.2f}%".format(100 * correct / len(test_set)))

7.3 sklearn实现KNN算法

参考来源链接: https://blog.csdn.net/codedz/article/details/108862498
1. sklearn中的KNN方法

sklearn.neighbors.KNeighborsClassifier(n_neighbors = 5,
                       weights='uniform',
                       algorithm = '',
                       leaf_size = '30',
                       p = 2,
                       metric = 'minkowski',
                       metric_params = None,
                       n_jobs = None
                       )

参数如下：

n_neighbors：这个值就是指 KNN 中的 “K”了。前面说到过，通过调整 K 值，算法会有不同的效果。

weights（权重）：最普遍的 KNN 算法无论距离如何，权重都一样，但有时候我们想搞点特殊化，比如距离更近的点让它更加重要。这时候就需要 weight 这个参数了，这个参数有三个可选参数的值，决定了如何分配权重。参数选项如下：
‘uniform’：不管远近权重都一样，就是最普通的 KNN 算法的形式。
‘distance’：权重和距离成反比，距离预测目标越近具有越高的权重。
自定义函数：自定义一个函数，根据输入的坐标值返回对应的权重，达到自定义权重的目的。

algorithm：在 sklearn 中，要构建 KNN 模型有三种构建方式

暴力法，就是直接计算距离存储比较的那种放松。

使用 kd 树构建 KNN 模型

使用球树构建。

其中暴力法适合数据较小的方式，否则效率会比较低。

如果数据量比较大一般会选择用 KD 树构建 KNN 模型，而当 KD 树也比较慢的时候，则可以试试球树来构建 KNN。参数选项如下：

‘brute’ ：蛮力实现

‘kd_tree’：KD 树实现 KNN

‘ball_tree’：球树实现 KNN

‘auto’：默认参数，自动选择合适的方法构建模型

不过当数据较小或比较稀疏时，无论选择哪个最后都会使用 ‘brute’

leaf_size：如果是选择蛮力实现，那么这个值是可以忽略的，当使用KD树或球树，它就是是停止建子树的叶子节点数量的阈值。默认30，但如果数据量增多这个参数需要增大，否则速度过慢不说，还容易过拟合。
p：和metric结合使用的，当metric参数是"minkowski"的时候，p=1为曼哈顿距离， p=2为欧式距离。默认为p=2。

metric：指定距离度量方法，一般都是使用欧式距离。
‘euclidean’ ：欧式距离
‘manhattan’：曼哈顿距离
‘chebyshev’：切比雪夫距离
‘minkowski’：闵可夫斯基距离，默认参数
n_jobs：指定多少个CPU进行运算，默认是-1，也就是全部都算。

属性如下:
classes_ : 分类器已知的类别标签，返回ndarray标签数组。
effective_metric_： 距离度量，和上述参数中metric参数设定的距离度量一致。
effective_metric_params_：指标函数附加的关键字参数，对于大多数距离指标，将会和metric参数相同，但如果effective_metric_params_属性设置为‘minkowski’，那么也可能包含p参数的值。返回的形式是字典。
outputs_2d_：训练时当y的形状为（n，）或（n，1），则返回False，否则返回True。

方法如下：
fit(X, y)：使用X作为训练数据，y作为标签目标数据进行数据拟合训练。
get_params([deep])：获取参数组成的字典。
kneighbors([X, n_neighbors, return_distance])：找寻一个点的k个邻居。
predict(X)：根据提供的数据去预测它的类别标签。
predict_proba(X)：返回测试数据X的概率估计值。
score(X, y[, sample_weight])：返回给定数据和标签的平均准确度。
set_params(params)：设置估值器的参数。

2. 交叉验证法选取最佳k值

from sklearn.datasets import load_iris
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier

#加载鸢尾花数据集
iris = load_iris()
x = iris.data
y = iris.target
k_range = range(1, 31) # 设置循环次数
k_error = []
#循环，取k从1~30，查看误差效果
for k in k_range:
    knn = KNeighborsClassifier(n_neighbors=k)
    #cv参数决定数据集划分比例，这里是按照5:1划分训练集和测试集
    scores = cross_val_score(knn, x, y, cv=6, scoring='accuracy')
    k_error.append(1 - scores.mean())

#画图，x轴为k值，y值为误差值
plt.plot(k_range, k_error)
plt.xlabel('Value of K in KNN')
plt.ylabel('Error')
plt.show()

输出结果：

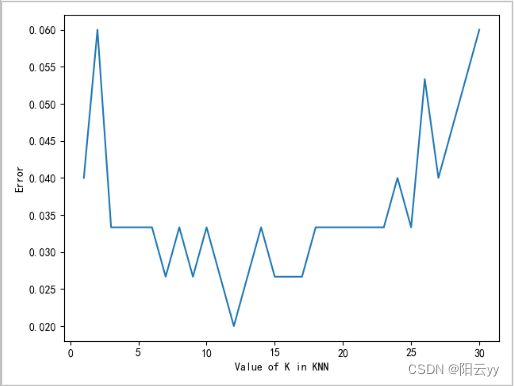
由这个图我们可以看出大致在k=11的时候，损失值是最小的，所以我们选择k = 11进行训练。

3. KNN测试

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn import neighbors, datasets

n_neighbors = 11

# 加载鸢尾花数据集
iris = datasets.load_iris()
# 选择其中的两个特征
X = iris.data[:, :2]
y = iris.target

h = .02 # 网格步长

# 创建色彩图
cmap_light = ListedColormap(['orange', 'cyan', 'cornflowerblue'])
cmap_bold = ListedColormap(['darkorange', 'c', 'darkblue'])

# 在两种权重下绘制图像
for weights in ['uniform', 'distance']:
	# 创建knn分类器实例, 并进行训练拟合
	clf = neighbors.KNeighborsClassifier(n_neighbors, weights = weights)
	clf.fit(X,y)

	 # 绘制决策边界
	x_min, x_max = X[:,0].min() - 1, X[:,0].max() + 1
	y_min, y_max = X[:,1].min() - 1, X[:,1].max() + 1
	xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
						 np.arange(y_min, y_max, h))
	Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
	
	Z = Z.reshape(xx.shape)
	plt.figure()
	plt.pcolormesh(xx, yy, Z, cmap = cmap_light)

	# 绘制训练点
	plt.scatter(X[:, 0], X[:, 1], c = y, cmap = cmap_bold, edgecolor='k', s=20)
	plt.xlim(xx.min(), xx.max())
	plt.ylim(yy.min(), yy.max())
	plt.title('3-Class classification (k = %i, weights = "%s")' % (n_neighbors, weights))

plt.show()