机器学习笔记-K-Means理论及实现

聚类算法

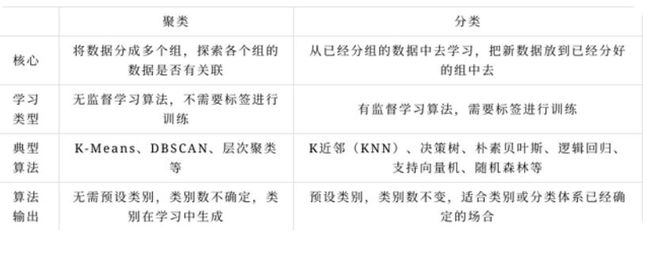
聚类算法与分类算法的区别如下所示：

聚类算法可以应用于寻找优质客户、社区发现、异常点监控等方面。

K-Means简介

K-Means算法是最简单的聚类算法，核心思想是以空间中k个点为中心进行聚类，对最靠近他们的对象归类。通过迭代的方法，逐次更新个聚类中心的值，直至得到最好的聚类结果。K-Means算法的具体过程如下所示：

1. 先从没有标签的元素集合A中随机取K个元素，作为K个子集各自的重心。
2. 分别计算剩下的元素到K个子集中心的距离（主要是欧式距离），根据距离将这些元素分别划归到最近的子集。
3. 根据聚类结果，重新计算重心（计算各个子集中所有元素的平均数）。
4. 将集合A中全部元素按照新的重心然后再重新聚类。
5. 重复第4步，直到聚类结果不再发生变化。

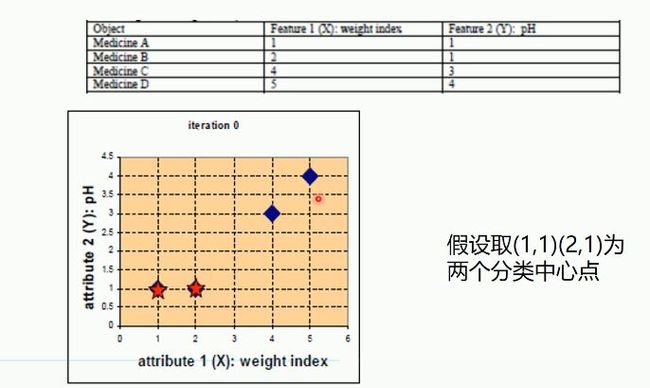
K-Means实例

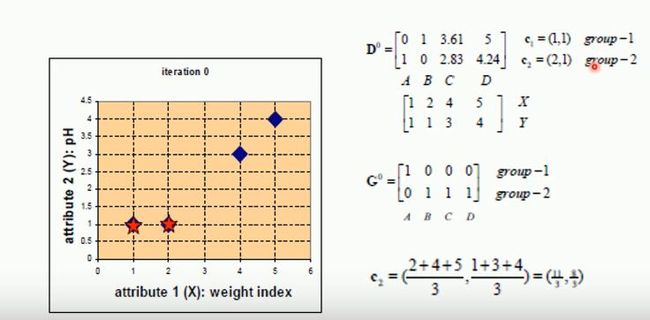
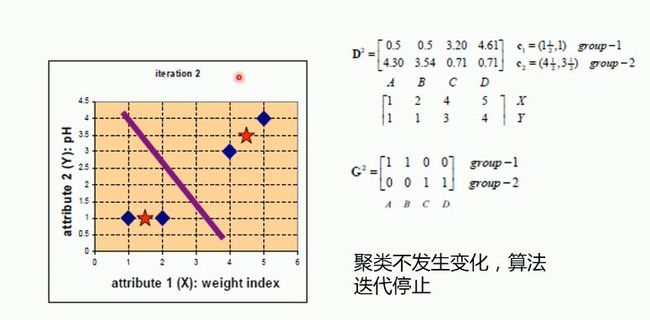
D0为各个点到中心点的距离。

G0为聚类后的结果，A为第一个类别，BCD为第二个类别。聚类完之后重新计算中心点C2 。计算为聚类中心后在重新进行聚类，如下图所示。

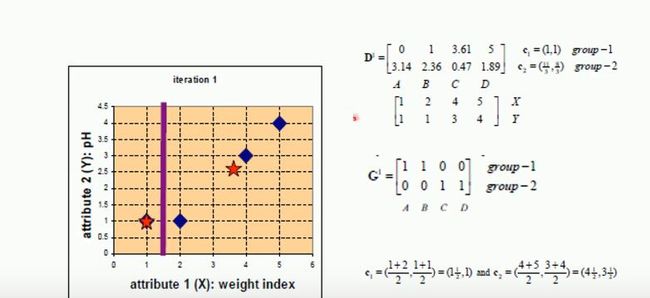
重新聚类后得到AB为第一个类别，CD为第二个类别。再重新计算聚类中心，如下图所示：

得到AB为第一类别，CD为第二类别。聚类中心点不再发生变化，算法迭代停止。

K-Means实现

导包

from sklearn.cluster import KMeans
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')

载入数据、建立模型并训练

#载入数据
data=np.genfromtxt("kmeans.txt",delimiter=" ")
#设置k值
k=4
#训练模型
model=KMeans(n_clusters=k)
model.fit(data)

输出聚类中心并输出预测结果

#分类中心点坐标
centers=model.cluster_centers_
print(centers)
#预测结果 
result=model.predict(data)
print(result)

画图

mark=['or','ob','og','ok']
#化样本点
for i,d in enumerate(data):
    plt.plot(d[0],d[1],mark[result[i]])
#用不同颜色形状来表示各个类别
mark=['*r','*b','*g','*k']
for i,center in enumerate(centers):
    plt.plot(center[0],center[1],mark[i],markersize=20)
plt.show()

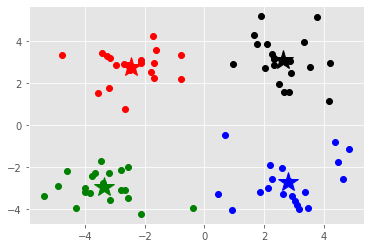
训练结果如下图所示：

画图

# 获取数据值所在的范围
x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1
y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1

# 生成网格矩阵
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
                     np.arange(y_min, y_max, 0.02))

z = model.predict(np.c_[xx.ravel(), yy.ravel()])# ravel与flatten类似，多维数据转一维。flatten不会改变原始数据，ravel会改变原始数据
z = z.reshape(xx.shape)
# 等高线图
cs = plt.contourf(xx, yy, z)
#显示结果
mark=['or','ob','og','ok']
#化样本点
for i,d in enumerate(data):
    plt.plot(d[0],d[1],mark[result[i]])
#用不同颜色形状来表示各个类别
mark=['*r','*b','*g','*k']
for i,center in enumerate(centers):
    plt.plot(center[0],center[1],mark[i],markersize=20)
plt.show()

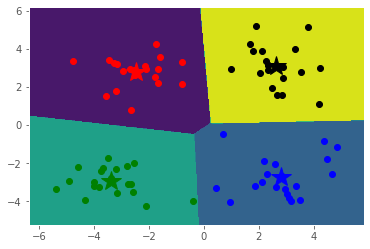
结果如下图所示：

K-Means存在的问题

1、对k个初始质心的选择比较敏感，容易陷入局部最小值。（不同的k值选取得到的结果不同）
2、k值的选择是用户指定的，不同的k得到的结果会有挺大的不同。
3、存在局限性，不能聚类非球形的数据。如下所示：

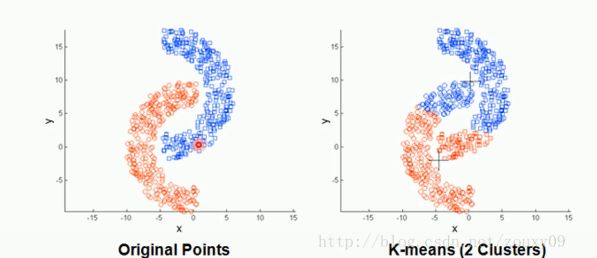
4、数据量较大时，收敛会比较慢。
对于存在的问题一，可以使用多次的随机初始化，计算每一次建模得到的代价函数的值，选取代价函数的最小结果作为聚类结果。其具体实现如下所示：

对于问题二的解决办法主要有两种：肘部法则和根据业务的需求。
使用肘部法则来选择k的值，如下所示：

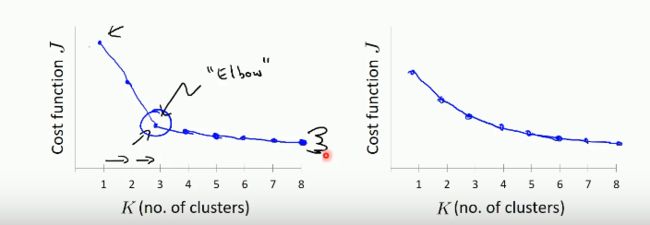
不同的k值得到的代价函数不同，k值越小，代价函数越大。

可视化K-Means

可视化K-Means网站：https://www.naftaliharris.com/blog/visualizing-k-means-clustering/

参考文献：https://baijiahao.baidu.com/s?id=1747494468301648417&wfr=spider&for=pc

参考视频：https://www.bilibili.com/video/BV1Rt411q7WJ?p=62&vd_source=166e4ef02c5e9ffa3f01c2406aec1508