忘掉Xavier初始化吧!最强初始化方法ZerO来了
文 | 小戏
谈及最典型的深度学习模型的训练,脑海里浮现的格式化的套路是什么?给定一个问题,给定一个数据集,弯弯绕绕确定好选择的神经网络的架构,然后上手调参,接下来的工作彷佛像是固定的重复工作,随机初始化参数,迭代训练,评估结果,直到一个模型新鲜出炉。
其实认真反思一下这套流水线的作业方法,其中的随机性主要集中在随机初始化参数上,如果再问一个为什么,为什么我们要随机初始化参数呢?答案可能是因为梯度下降法总是需要给这些权重参数一个值,如果我们延用逻辑回归中令初始权重都为 0 的做法,在梯度下降的过程里将无法对权重带来任何更新。那么一个简单的方式就是随机,但是随机是一个相对模糊的概念,但是显然,无论是理论上还是经验上都可以观察到,随机初始化权重的好坏可以极大的影响神经网络模型的收敛,同时,过大的参数将会导致梯度爆炸,而过小的参数将会导致梯度消失,方差的不合理也会导致神经网络模型难以稳定,因此,一个合理的规范的参数对模型的训练而言变得尤为重要,从而使得各种 Norm 方法在深度学习中扮演着越来越重要的角色。

基于这些经验式的法则,便用于了种种参数随机初始化的方法,诸如 Xavier 初始化,He 初始化等等,这些参数初始化的方式的优势几乎都集中于去稳定一个良好的方差,尽管在很大程度上解决了参数“稳定性”的问题,但是“随机性”的问题仍然存在,随机数种子也不可避免的成为了一种另类的“超参数”。
而今天的这篇文章,则切换了思路,如果可以用一种完全确定的参数初始化方法,去满足这些对于初始权重在信号传播与梯度下降里的要求,那么是不是可以在一举解决参数随机初始化的问题,为模型带来随机初始化参数所不具备的更好的性能呢?这篇 TMLR 的论文提出了一种名为 ZerO 的初始化方法,仅仅使用 0 和 1 做初始化,在抛弃了 Batch Norm 层的情况下仍然可以训练 500 层级别的模型,并且应用于 ResNet 在多个数据集上刷新了 SOTA ,并证明了这种确定性的初始化方法的诸多好处。
论文题目:
ZerO Initialization: Initializing Neural Networks with only Zeros and Ones
论文链接:
https://openreview.net/pdf?id=1AxQpKmiTc
 1. 从恒等初始化开始
1. 从恒等初始化开始
困扰随机初始化方法的很关键的一点在于如何使得神经网络各层参数之间的方差不发生变化,那么一种简单的思路便是让各层之间的权重完全相等,并且使得上一层的输入“完整”的传入下一层,这样方差便不再成为一个需要考虑的问题。那么很自然的,便是将神经网络的权重层初始化为一个单位矩阵,这种初始化方法被称为恒等初始化(Identity Initialization)。在理论上恒等初始化具有相当好的性质,这种性质被称为动力等距(Dynamical Isometry),最早由 Saxe 等人在2014年提出,它描述了当输入输出的雅可比矩阵的奇异值分布全部在 1 附近时,即 (这里 表示输出向量, 表示输入向量)时,神经网络具有稳定的信号传播以及梯度下降的行为,可以期待具有良好的训练表现。显然,单位矩阵 天然的满足动力等距的条件,但是恒等初始化优美的理论推导却都建立在各层的维度是相等的假设之上,但显然在实际中,这种假设有些过强使得它没法真正用于实际工作之中。
从恒等初始化的思想出发,一种显然的改进方式是部分单位矩阵(Partial Identity Matrix),它的定义十分自然,对于行列中“超出”的部分补零即可:

然而,当使用部分单位矩阵在训练诸如 ResNet 等经典结构中时,往往将会出现一种所谓“训练衰减(Training Degeneracy)”的现象,这种现象可以做如下描述:
假设 是一个 层的神经网络,对于 有 ,而对于 ,有 ,对于 有 。这里的 是神经网络的参数矩阵, 具有相同的隐藏层维度 ,输入数据维度为 ,输出数据的维度为 ,此处假设 ,定义余项 ,令 为第 层的激活函数,当初始化 , 时,对于任意 ,将有:
这即表明,无论隐藏层维度有多高,神经网络 的维度仅仅依赖于输入数据的维度 ,从而极大的限制了神经网络的表达能力。
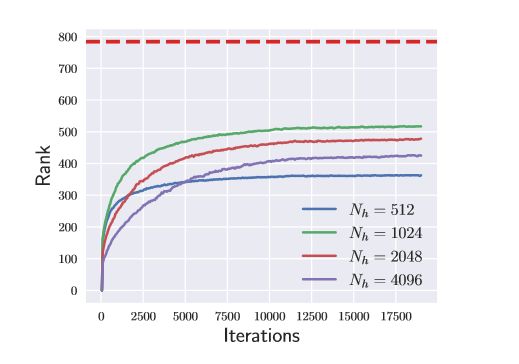
如上图所示,使用部分单位矩阵初始,在 MINST 上使用一个 3 层的神经网络进行训练,红色虚线表示 的维度为 784 ,可以看出,无论 的维度有多大, 的秩在训练过程在始终低于 的维度。
 2. 哈达玛变换与 ZerO
2. 哈达玛变换与 ZerO
为了避免直接使用部分单位矩阵作为初始权重参数进行训练而出现的训练衰减问题,论文作者提出了使用哈达玛变换(Hadamard Transform)来初始化权重参数,熟悉图像的小伙伴也许对哈达玛矩阵并不陌生,哈达玛变换常用作图像与视频编码,哈达玛矩阵是均由+1与-1的元素构成,且满足 。哈达玛矩阵可以通过递归的构造得到,设 ,则有:
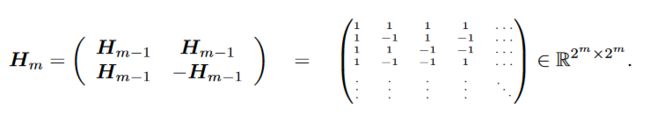
哈达玛变换即使用哈达玛矩阵进行的线性变换,直观上讲,在二维平面中,哈达玛变换可以将标准坐标轴旋转45度,论文作者证明了针对部分单位矩阵应用哈达姆变换,即 ,可以有效的规避训练衰减对神经网络训练带来的伤害,即,当初始化权重为 , 时,对于任意 ,将有:
应用哈达玛变换的权重神奇的打破了训练衰减 ,区别于随机初始化权重,随机初始化权重生效由于构造的一个随机权重矩阵可以被认作按列线性无关的,从而可以认为:
而哈达玛变换从另一个方面规避了训练衰减的问题,本质上来讲,部分单位矩阵的训练衰减主要是源自于“补零”的操作,使得这些位置的输入在激活函数阶段无法生效,从而使得维度被 限制,而哈达玛变换通过将基向量“旋转”,打破了在传递过程中零元素的对称性,从而解决了训练衰减的问题。而这种“旋转”方式的选择显然不止一种,但是作者认为哈达玛变换是最自然的一种选择,以上文中的 MNIST 上训练的三层网络为例,下图展现了哈达玛变换打破训练衰减的直观图例:

通过哈达玛变换解决训练衰减的问题后,结合恒等初始化,作者构建了 ZerO 初始化方法,具体算法步骤如下图所示:

 3. 数值实验
3. 数值实验
这篇论文通过将 ZerO 初始化分别用于 ResNet-18 与 ResNet-50 在 CIFAR-10 与 ImageNet 数据集上进行训练,实验结果如下图所示:
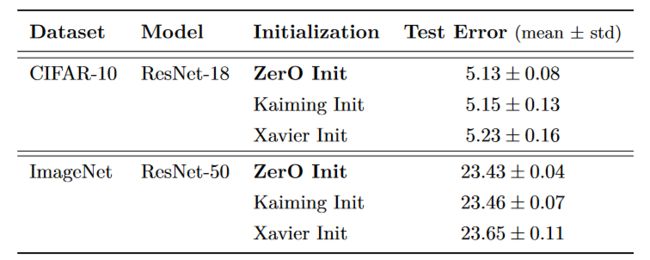
通过对比 Kaiming Init 与 Xavier Init,可以看到在测试误差上 Zero Init 在两个数据集上均取得了更好的效果。
同时,通过将 ZerO 方法与其他权重初始化方法进行对比,在 ResNet-18 与 ResNet-50 网络上,ZerO 方法均取得了更好的表现:

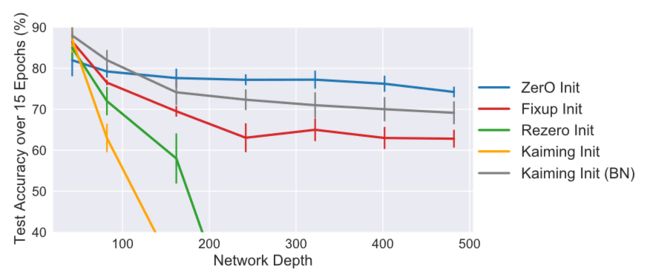
并且,对比其他权重初始化方法,ZerO 方法还可以训练更深的网络,在没有使用 batch normalization 的情况下,在 CIFAR-10 数据集上成功训练出了 500 层深的 ResNet 网络:
最后,作者还将 ZerO 方法成功用于了 Transformer 之中,通过使用 ZerO 初始化多头注意力与前馈层权重,并在多头注意力中将 固定为单位矩阵, 与 固定为零。在 WikiText-2 数据集上,对比标准的权重初始化方法,ZerO 不仅可以训练出 20 层的 Transformer ,并且在大部分情况下表现也优于标准的权重初始化方法。

综合来讲,ZerO 在诸如超参数设置、模型深度等方面均具有其余模型所不具备的优良特性,并且,由于其确定性的权重初始化方法,也使得使用 ZerO 方法训练得到的结果在重复训练的过程中变换程度更低,因此也使得使用 ZerO 方式训练出的模型更具可复现性。
 4. GLRL
4. GLRL
在 ZerO 的性能之外,论文作者在 ZerO 的训练过程中发现了一个更加有趣的现象,被称为低秩的学习轨迹(Low-Rank Learning Trajectory),这点在前面的图表中就已经可以露出端倪:
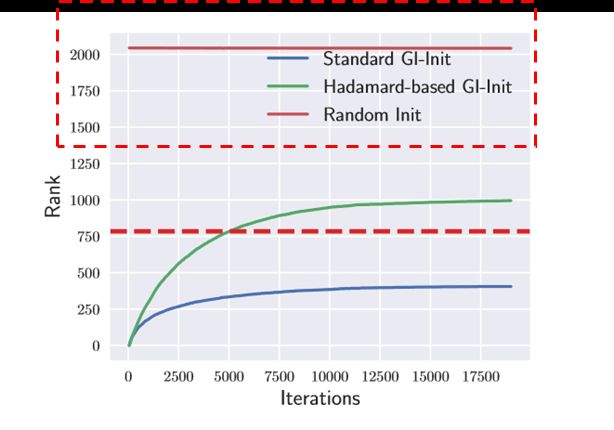
可以看到,使用哈达玛变换作为初始权重的训练过程与使用随机初始化权重的训练过程有很大区别,相较于随机初始化权重一开始就训练一个较为“复杂”(权重秩很大)的网络,ZerO 一开始似乎在训练一个更为“简单”的网络,并在不断的学习过程中逐渐使得网络变得“复杂”。
为了展示这种现象,作者通过定义:
来衡量稳定时的权重矩阵的秩,从而侧面反映网络的复杂度,此处的 表示矩阵的奇异值,通过计算 ZerO 与其他随机初始化方法的稳定秩,可以得到如下图的结果:
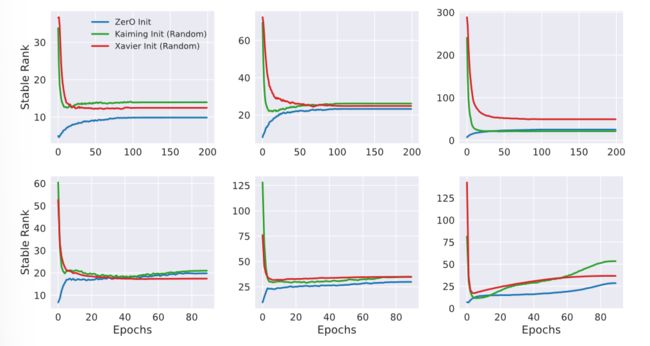
上层图表示 ResNet-18 在 CIFAR-10 的训练结果,下层图表示 ResNet-50 在 ImageNet 的训练结果,从左到右分别提取了 ResNet 第二、三、四组残差块的第一层卷积,可以看到,ZerO 初始化具有明显的低秩学习的特征。
论文作者指出,这是第一次在实际算例中观察到这种贪心的低秩学习(greedy low-rank learning,GLRL)现象,GLRL 是一种梯度下降的理论特征,它展现了当初始化权重为无穷时,梯度下降隐含地偏好于简单的解决方案,即在梯度下降过程中,偏好以权重矩阵的秩递增的顺序在解空间中搜索,在低秩空间无法找到最小值后,才转去高秩空间进行搜索。
GLRL 现象可以帮助解释基于梯度下降法的神经网络卓越的泛化能力以及经常收敛到低秩的全局或局部最优解之中。然而在理论推导中假设初始化权重为无穷大,这在实际中无法应用与观察,但是,ZerO 成功证明了 GLRL 现象不仅仅存在于初始权重无穷的假设之中,同时也在恒等初始化之中有类似的效果。
 4. 结论与思考
4. 结论与思考
针对深度神经网络的理论研究如火如荼,这篇论文事实上从某种程度上讲是在这些神经网络理论的指导下的探索之作,在恒等初始化动力等距的优良性质下利用哈达玛变换将其进行扩展,在得到了一个表现优异的初始化方法的基础上,还验证了 GLRL 现象在现实中的存在。
尽管就目前而言,神经网络的理论研究还不如物理学一样有一座“坚硬的大厦”,但是从这篇论文可以看出它已然可以在高点为我们的工作提出一点建议与指导,其实与其麻木的将深度学习模型的训练作为流水线上的拧螺丝安螺帽,不如从这种固定的“套路”中跳出来看看这整个工厂各个机器实际的运营运转的方式方法,这或许需要亿点点数学思维,但这又何尝不是学习神经网络这样一个未知黑盒的乐趣所在呢?
边学语言学边学NLP~
作品推荐
千呼万唤始出来——GPT-3终于开源!
NLP哪个细分方向最具社会价值?
吴恩达发起新型竞赛范式!模型固定,只调数据?!
仅仅因为方法 Too Simple 就被拒稿,合理吗?
算法工程师的三观测试
加入卖萌屋NLP、CV、搜推广与求职讨论群


